描述性指標
出自 MBA智库百科(https://wiki.mbalib.com/)
目錄 |
什麼是描述性指標[1]
描述性指標是指反映社會現象實際情況的指標,如:城鎮人口數、居民擁有電腦數、財政收入總額等等。
描述性指標的內容[2]
描述指標是用於反映社會經濟現象總體客觀狀況,反映社會經濟活動的條件、過程和結果的統計指標。例如,反映社會經濟活動條件的指標,如各種自然資源擁有量指標、土地面積指標、勞動力資源指標、科技力量指標等等;反映社會經濟活動過程和結果的指標,如社會總產值;國民收入、國民生產總值、固定資產、物資的增加量、減少量和庫存量、進出口貿易額、利潤額、財政收入與支出等等;反映社會物質文化生活狀況的指標,如居民平均收入與支出、居民文化程度、在校學生數、醫療機構及床位數、文化娛樂設施等指標。這類指標提供對社會經濟活動狀況的基本認識,是統計信息的主體。
統計描述指標及其選用原則[3]
統計描述是統計分析的重要組成部分,是統計推斷的基礎,它是指用統計表和統計圖或利用統計指標來描述資料的特征。
(一)數值變數的統計學描述
數值變數也叫做計量資料,是對觀察對象的某個指標採用度(衡)量的方法進行檢測所得到的資料。數值變數資料的統計描述主要包括以下幾個方面。
1.頻數表。包括頻數又稱頻率,是指某一變數觀察結果在某一特定數值(或數值範圍內)出現的次數。將事物分類之後統計出來的各類頻數排列成表格,即為頻數表。利用頻數分析,可從一大堆變數觀測值中直觀地瞭解變數的分佈特征。
(1)頻數表的編製方法。
1)求極差 找出觀察值中的最大值和最小值,利用以下公式計算:
極差=最大值-最小值
2)確定組距和各組段的上下限 為了簡化資料,顯示數據的分佈規律,對極差進行分割分組。適宜的分組數與觀察值的個數的多少有關,一般觀察值在30左右時,可分為5~6組,隨觀察值的增加,分組數可增加。組數一般為8~15組。
3)列表劃記落在各組段內的觀察值個數(頻數)。
根據編製出的頻數表即可瞭解該數值變數資料的頻數分佈特征。
(2)頻數分佈的特征及類型:
2)兩種類型:對稱分佈和偏態分佈,偏態分佈又有正偏態和負偏態之分。
(3)頻數表的用途:①描述資料的分佈特征和分佈類型。②為進一步計算有關指標或進行統計分析提供依據。③便於發現特大或特小的可疑值。④繪製頻數分佈圖。
2.集中趨勢的描述。描述一組觀察值分佈集中位置或平均水平的指標稱為平均數。它能使人對資料有個簡明概括的印象,並能進行資料問的比較。常用的平均數有算術平均數、幾何均數和中位數。
(1)算術平均數。算術平均數簡稱均數,有總體平均數(μ)和樣本平均數( )之分,平均數描述一組數據在數量上的平均水平。樣本均數的計算公式為:
)之分,平均數描述一組數據在數量上的平均水平。樣本均數的計算公式為: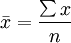
均數適用於表示對稱分佈,特別是正態分佈的資料的、F均水平,不適用於偏態分佈的資料。如有數據3、4、5、6、12,可見數據多在3~6之間,但均數為6,顯然不能代表這組數據的中心位置,此時應用中位數描述其集中趨勢。
(2)幾何均數。幾何均數適用於原始數據分佈不對稱,但經對數轉換後呈對稱分佈的資料。這類資料可以是呈倍數關係的等比資料,如醫學上血清抗體滴度資料。在應用中應註意觀察值不能同時有正有負,同一資料算得的幾何均數小於算術平均數。計算公式為:![G=\sqrt[n]{x_1x_2\ldots x_n}](/w/images/math/a/d/0/ad082e6a533d98962380e41e94c15caa.png)
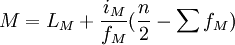
式中:LM為中位數所在組段的下限,iM為中位數所在組段的組距,fM為中位數所在組段的頻數,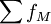 知為中位數所在組段的以前的累計頻數。
知為中位數所在組段的以前的累計頻數。
中位數用於描述偏態分佈資料的集中位置,它不受兩端特大、特小值的影響,當分佈末端無確切數據時也可計算。同時任何分佈的定量數據均可用中位數描述其分佈的集中趨勢,適用範圍較廣。
3.離散程度的描述。集中趨勢是數據分佈的一個重要特征,但單有集中趨勢指標還不能很好地描述數據的分佈規律。為了比較全面地描述數據分佈的規律,除了需要有描述集中趨勢的指標外,還需引入描述數據分佈離散程度的指標。描述離散趨勢的指標有多種,最常用的有極差、四分位數間距、方差、標準差和變異繫數。
(1)極差。又稱全距,即最大和最小觀察值之間的間距,用極差描述資料的離散程度簡單明瞭,但它不能反映觀察值的整個變異度,而且樣本的例數越多,極差的可能就越大,因此用極差來描述離散趨勢就不夠穩定,易受奇異值的影響。
(2)四分位數間距。四分位數是特定的百分位數,其中P25為下四分位數Ql,P75為上四分位數Qu。四分位數間距即Qu − Ql。四分位數間距比極差穩定,是兩個統計學點值之間的距離,但仍未考慮每個觀察值的變異度。
(3)方差。離均差的絕對值之和或離均差平方和(SS)可用來描述資料的變異度。SS的均數(即均方)不受觀察值個數的影響,用來描述資料的離散程度較離均差的絕對值之和或離均差平方和更好。方差也有總體方差和樣本方差之分。樣本方差的計算公式為: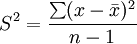
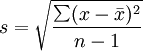
標準差可用於描述變數值的離散程度,與均數結合還可描述資料的分佈情況,此外還可用於求參考值範圍和計算標準差。
(5)變異繫數。在比較多組資料的離散程度時,如這兒組資料的單位不同或均數相差懸殊時,用標準差就不合適。此時需要用到變異繫數又稱離散繫數來比較,它實際上是標準差占均數的百分比例。計算公式為:
CV=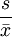 ×100%
×100%
(二)分類變數的統計學描述
對分類變數資料進行統計描述的一般步驟,是先對觀察測量得到的變數值(即觀察值)進行分類彙總(即“計數”)得到分類資料頻數表(屬於絕對數指標),再在此基礎上計算相對數指標(即兩個指標之比)才能對分類變數資料進行正確的描述。
1.常用的相對數指標。
(1)率:又稱頻率指標,用來說明某現象發生的頻率或強度。計算公式為:
率=發生某現象的觀察單位數÷可能發生某現象的觀察單位總數×k
式中:k可為100%、萬/萬等。
如某居民區的年平均人口數為36 723人,經檢查該區患急性傳染病的人口數為433人,則某居民區該年急性傳染病發病率為:117.9/萬[(433/36 723)×(萬/萬)]。
(2)構成比:又稱構成指標。其計算公式為:
構成比=某一組成部分的觀察單位數÷同一事物個組成部分的觀察單位總數×100%
構成比用來說明事物內部各組成部分所占比重或分佈。如某市的急性傳染病發病數為2 884人,其中有A居民區急性傳染病發病數為545人,則該居民區占全市急性傳染病發病數的比重為18.9%(545/2 884×100%)。事物內部各構成比之和必為1。
(3)比:又稱相對比,為兩個相對數之比。其基本計算公式為:比=A/B
說明A為B的若幹倍或百分之幾。A、B可為絕對數、相對數或平均數。如某市某年A區的急性傳染病發病數為433人,B區的急性傳染病發病數為541人,則B區與A區急性傳染病發生數之比為1.25(541/433)。
2.應用相對數時應註意的問題。
(1)計算相對數時,分母不宜過小。
(2)構成比和率不能相互混淆。兩者的區別如表1:
表1
| 構成比 | 率 | |
|---|---|---|
| 概念 | 說明事物內部組成部分所占比重或分佈 | 說明某現象發生的頻率或強度 |
| 合計 | 100% | 分率不能直接相加 |
| 改變 | 任一部分比重的增減都會影響其他部分的比重 | 某一分率改變對其他分率無影響 |
(3)求平均數或總率時,分子、分母應分別相加,然後按相對數的計算公式重新計算。
(4)註意資料同質性、可比性。
(5)樣本率或構成比的比較應建立在隨機抽樣的基礎上,並作假設檢驗。
3.動態數列。
(1)概念:動態數列是一系列按時間順序排列的統計指標(可以是絕對數、相對數或平均數),用以說明事物在時間上的:變化和趨勢。
(2)常用的分析指標:
1)絕對增長量,有累計年增長和逐年增長之分;
2)發展速度與增長速度,其中定基比描述變化趨勢.環比用來描述指標的逐年波動情況;
3)平均發展速度和平均增長速度,其中平均發展速度是第n年指標除以基期指標的商再開n次方。
平均增長速度=平均發展速度-1(100%)
4.率的標準化。
(1)意義和基本思想:率的標準化可在比較總率時消除混雜因素(即內部構成不同)的影響,用標準化法將資料變換為符合可比條件。經常需要標化的指標有人口死亡率、病死率、發病率等,常見的混雜因素有年齡、病情等。
(2)標準率的計算步驟:
1)選取標準:常選用全世界、全國或本地區範圍較大人群作為標準,此類標準最好。實踐中也常用被標化組的合計作為標準。有時也會任選一組被標化組作為標準,但效果往往較差。
2)根據現有數據選用方法:
·直接法:已知標準人口數或標準人口年齡構成,被標化組需要知道各年齡組的率。以死亡率為例,當已知標準組的年齡別、人口數時,其計算公式為: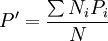
式中:P'為標準化率,Ni為標準組第i個年齡組的人口數,Pi為被標化組第i個年齡組的死亡率,N為標準組的總人數,
當已知標準組的年齡別、人口構成時,其計算公式為: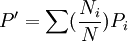
式中:P'為標準化率,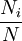 為標準組第i個年齡組的人口構成比,Pi為被標化組的死亡率。
為標準組第i個年齡組的人口構成比,Pi為被標化組的死亡率。
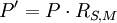
式中:P為標準組的總死亡率,RS,M為標化死亡比——是指被標化組實際死亡數與預期死亡數之比。
(3)應用註意事項:①標化率沒有實際意義,僅作比較之用;②資料若為樣本資料,則標化率的比較仍需假設檢驗;③當各年齡組的率有明顯交叉時不宜採用標準化法。







