四分位數

用手机看条目

出自 MBA智库百科(https://wiki.mbalib.com/)

四分位數（Quartile）

什麼是四分位數

　　分位數根據其將數列等分的形式不同可以分為中位數，四分位數，十分位數、百分位數等等。四分位數作為分位數的一種形式，在統計中有著十分重要的意義和作用。

　　人們經常會將數據劃分為4個部分，每一個部分大約包含有1/4即25％的數據項。這種劃分的臨界點即為四分位數。它們定義如下：

$Q 1$ =第1四分位數，即第25百分位數；
$Q 2$ =第2四分位數，即第50百分位數；
$Q 3$ =第3四分位數，即第75百分位數。

[編輯]

四分位數的計算^[1]

　　（一）根據未分組的資料計算四分位數

　　第一步：確定四分位數的位置。

　　四分位數是將數列等分成四個部分的數，一個數列有三個四分位數，設下四分位數、中位數和上四分位數分別為 $Q 1$ 、 $Q 2$ 、 $Q 3$ ，則： $Q 1$ 、 $Q 2$ 、 $Q 3$ 的位置可由下述公式確定：

　　 $Q 1$ 的位置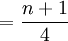 $=\frac{n+1}{4}$

　　 $Q 2$ 的位置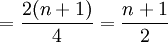 $=\frac{2(n+1)}{4}=\frac{n+1}{2}$

　　 $Q 3$ 的位置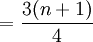 $=\frac{3(n+1)}{4}$

　　式中n表示資料的項數

　　第二步：根據第一步所確定的四分位數的位置，確定其相應的四分位數。

　　例如：某車間某月份的工人生產某產品的數量分別為13、13.5、13.8、13.9、14、14.6、14.8、15、15.2、15.4、15.7公斤，則三個四分位數的位置分別為：

　　 $Q 1$ 的位置 $=\frac{n+1}{4}=\frac{(11+1)}{4}=3$

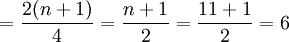
　　 $Q 2$ 的位置 $=\frac{2(n+1)}{4}=\frac{n+1}{2}=\frac{11+1}{2}=6$

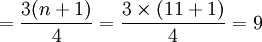
　　 $Q 3$ 的位置 $=\frac{3(n+1)}{4}=\frac{3\times(11+1)}{4}=9$

　　即變數數列中的第三個、第六個、第九個工人的某種產品產量分別為下四分位數、中位數和上四分位數。即：

　　 $Q 1 = 13.8$ 公斤、 $Q 2 = 14.6$ 公斤、 $Q 3 = 15.2$ 公斤

　　上例中（n+1）恰好為4的倍數，所以確定四分數較簡單，如果（n+1）不為4的整數倍數，按上述分式計算出來的四分位數位置就帶有小數，這時，有關的四分位數就應該是與該小數相鄰的兩個整數位置上的標誌值的平均數，權數的大小取決於兩個整數位置距離的遠近，距離越近，權數越大，距離越遠，權數越小，權數之和等於1。

　　例如：某車間某月份的工人生產某產品的數量分別為13、13.5、13.8、13.9、14、14.6、14.8、15、15.2、15.4公斤，則三個四分位數的位置分別為：

　　 $Q 1$ 的位置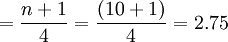 $=\frac{n+1}{4}=\frac{(10+1)}{4}=2.75$

　　 $Q 2$ 的位置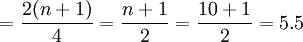 $=\frac{2(n+1)}{4}=\frac{n+1}{2}=\frac{10+1}{2}=5.5$

　　 $Q 3$ 的位置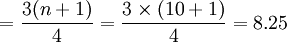 $=\frac{3(n+1)}{4}=\frac{3\times(10+1)}{4}=8.25$

　　即變數數列中的第2.75項、第5.5項、第8.25項工人的某種產品產量分別為下四分位數、中位數和上四分位數。即：

　　 $Q 1$ =0.25×第二項+0.75×第三項=0.25×13.5+0.75×13.8=13.73(公斤)

　　 $Q 2$ =0.5×第五項+0.5×第六項=0.5×14+0.5×14.6=14.3(公斤)

　　 $Q 3$ =0.75×第八項+0.25×第九項=0.75×15+0.25×15.2=15.05(公斤)

　　在實際資料中，由於標誌值序列中的相鄰標誌值往往是相同的，因而不一定要通過計算才能得到有關的四分位數。

　　（二）由組距式數列確定四分位數

　　第一步，向上或向下累計次數。

　　第二步，根據累計次數確定四分位數的位置。

　　1）當採用向上累計次數的資料確定四分位數時，四分位數位置的公式是：

　　 $Q 1$ 的位置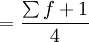 $=\frac{\sum f+1}{4}$

　　 $Q 2$ 的位置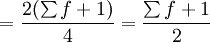 $=\frac{2(\sum f+1)}{4}=\frac{\sum f+1}{2}$

　　 $Q 3$ 的位置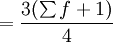 $=\frac{3(\sum f+1)}{4}$

　　式中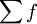： $\sum f$ 表示資料的總次數。

　　2）當採用向下累計次數的資料確定四分位數時，四分位數位置的公式是：

　　 $Q 1$ 的位置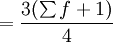 $=\frac{3(\sum f+1)}{4}$

　　 $Q 2$ 的位置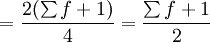 $=\frac{2(\sum f+1)}{4}=\frac{\sum f+1}{2}$

　　 $Q 3$ 的位置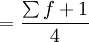 $=\frac{\sum f+1}{4}$

　　式中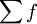： $\sum f$ 表示資料的總次數。

　　第三步，根據四分位數的位置算出各四分位數。

　　1）當累計次數是向上累計時，按下限公式計算各四分位數。

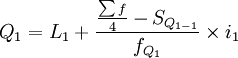
　　 $Q_1=L_1+\frac{\frac{\sum f}{4}-S_{Q_{1-1}}}{f_{Q_1}}\times i_1$

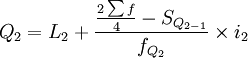
　　 $Q_2=L_2+\frac{\frac{2\sum f}{4}-S_{Q_{2-1}}}{f_{Q_2}}\times i_2$

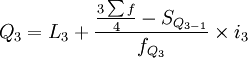
　　 $Q_3=L_3+\frac{\frac{3\sum f}{4}-S_{Q_{3-1}}}{f_{Q_3}}\times i_3$

　　式中： $Q 1$ 、 $Q 2$ 、 $Q 3$ 分別表示下四分位數、中位數和上四分位數；

　　 $L 1$ 、 $L 2$ 、 $L 3$ 分別表示下四分位數、中位數和上四分位數所在組的下限；

　　 $i 1$ 、 $i 2$ 、 $i 3$ 分別表示下四分位數、中位數和上四分位數所在組的組距；

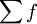　　 $\sum f$ 表示總次數；

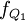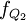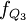　　 $f_{Q_1}$ 、 $f_{Q_2}$ 、 $f_{Q_3}$ 分別表示下四分位數、中位數和上四分位數所在組的次數；

　　 $S Q 1 - 1$ 表示下四分位數前一組的累計次數；

　　 $S Q 2 - 1$ 表示中位數前一組的累計次數；

　　 $S Q 3 - 1$ 表示上四分位數前一組的累計次數。

　　2）當累計次數是向下累計時，按上限公式計算各四分位數。

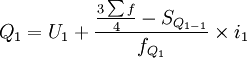
　　 $Q_1=U_1+\frac{\frac{3\sum f}{4}-S_{Q_{1-1}}}{f_{Q_1}}\times i_1$

　　 $Q_2=U_2+\frac{\frac{2\sum f}{4}-S_{Q_{2-1}}}{f_{Q_2}}\times i_2$

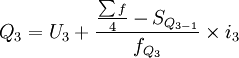
　　 $Q_3=U_3+\frac{\frac{\sum f}{4}-S_{Q_{3-1}}}{f_{Q_3}}\times i_3$

　　式中： $Q 1$ 、 $Q 2$ 、 $Q 3$ 分別表示下四分位數、中位數和上四分位數；

　　 $U 1$ 、 $U 2$ 、 $U 3$ 分別表示下四分位數、中位數和上四分位數所在組的上限；

　　 $i 1$ 、 $i 2$ 、 $i 3$ 分別表示下四分位數、中位數和上四分位數所在組的組距；

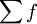　　 $\sum f$ 表示總次數；

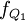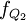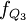　　 $f_{Q_1}$ 、 $f_{Q_2}$ 、 $f_{Q_3}$ 分別表示下四分位數、中位數和上四分位數所在組的次數；

　　 $S Q 1 - 1$ 表示下四分位數後一組的累計次數；

　　 $S Q 2 - 1$ 表示中位數後一組的累計次數；

　　 $S Q 3 - 1$ 表示上四分位數後一組的累計次數。

　　例如：某企業職工按月工資的分組資料如下：

按月工資分組（元）	職工人數（人）	向上累計職工人數	向下累計職工人數
600以下	23	23	566
600—700	120	143	543
700—800	150	293	423
800—900	135	428	273
900—1000	95	523	138
1000以上	43	566	43
合計	566	——	——

　　根據上述資料確定某企業職工的月工資的三個四分位數如下：

　　1）採用向上累計職工人數的資料得月工資四分位數的位置為：

　　 $Q 1$ 的位置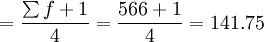 $=\frac{\sum f+1}{4}=\frac{566+1}{4}=141.75$

　　 $Q 2$ 的位置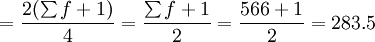 $=\frac{2(\sum f+1)}{4}=\frac{\sum f+1}{2}=\frac{566+1}{2}=283.5$

　　 $Q 3$ 的位置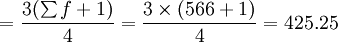 $=\frac{3(\sum f+1)}{4}=\frac{3\times(566+1)}{4}=425.25$

　　根據計算結果可知， $Q 1$ 、 $Q 2$ 、 $Q 3$ 分別位於向上累計職工人數的第二組、第三組和第四組，月工資四分位數分別為：

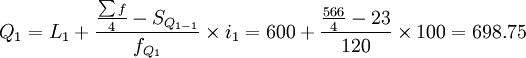　　 $Q_1=L_1+\frac{\frac{\sum f}{4}-S_{Q_{1-1}}}{f_{Q_1}}\times i_1=600+\frac{\frac{566}{4}-23}{120}\times 100=698.75$ (元)

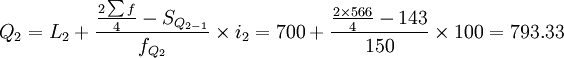　　 $Q_2=L_2+\frac{\frac{2\sum f}{4}-S_{Q_{2-1}}}{f_{Q_2}}\times i_2=700+\frac{\frac{2\times 566}{4}-143}{150}\times 100=793.33$ (元)

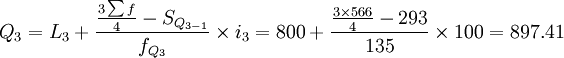　　 $Q_3=L_3+\frac{\frac{3\sum f}{4}-S_{Q_{3-1}}}{f_{Q_3}}\times i_3=800+\frac{\frac{3\times 566}{4}-293}{135}\times 100=897.41$ (元)

　　2）採用向下累計職工人數的資料得月工資四分位數的位置為：

　　 $Q 1$ 的位置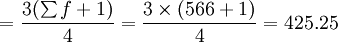 $=\frac{3(\sum f+1)}{4}=\frac{3\times(566+1)}{4}=425.25$

　　 $Q 2$ 的位置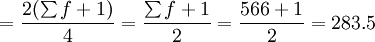 $=\frac{2(\sum f+1)}{4}=\frac{\sum f+1}{2}=\frac{566+1}{2}=283.5$

　　 $Q 3$ 的位置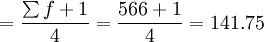 $=\frac{\sum f+1}{4}=\frac{566+1}{4}=141.75$

　　同樣可知： $Q 1$ 、 $Q 2$ 、 $Q 3$ 分別位於向下累計職工人數的第二組、第三組和第四組，月工資四分位數分別為：

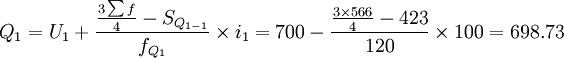　　 $Q_1=U_1+\frac{\frac{3\sum f}{4}-S_{Q_{1-1}}}{f_{Q_1}}\times i_1=700-\frac{\frac{3\times 566}{4}-423}{120}\times 100=698.73$ (元)

　　 $Q_2=U_2+\frac{\frac{2\sum f}{4}-S_{Q_{2-1}}}{f_{Q_2}}\times i_2=800-\frac{\frac{2\times 566}{4}-273}{150}\times 100=793.33$ (元)

　　 $Q_3=U_3+\frac{\frac{\sum f}{4}-S_{Q_{3-1}}}{f_{Q_3}}\times i_3=900-\frac{\frac{566}{4}-138}{135}\times 100=897.41$ (元)

　　計算結果同按下限公式計算的一致，即所求某企業職工月工資的三個四分數也分別為698.75元、793.33元和897.41元。

[編輯]

四分位數的案例分析

[編輯]

案例一^[2]

　　有l9名工人時產量件數為：14、15、16，16．17、18、18、19、19、20．2l，11、22、22、23、24、24、25、26，用n代表總體單位數。用 $Q 1$ 、 $Q 2$ 、 $Q 3$ 分別代表第一個、第二個和第三個四分位數。這三個四分位數的位置及其數值，可按下列公式算出：

　　 $Q 1$ 位置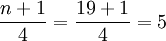 $\frac{n+1}{4}=\frac{19+1}{4}=5$ ,則 $Q 1$ =17件；

　　 $Q 2$ 位置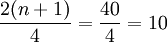 $\frac{2(n+1)}{4}=\frac{40}{4}=10$ ，則 $Q 2$ ＝20件；

　　 $Q 3$ 位置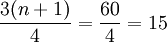 $\frac{3(n+1)}{4}=\frac{60}{4}=15$ ，則 $Q 3$ ＝23件。

　　四分位數間距= $Q 3 - Q 1$ ＝23-17＝6件。四分位差= $\frac{Q_3-Q_1}{2}$ =6÷2＝3件。通過第一四分位數17件，可以說明有1／4的工人時產量小於17件，有3／4的工人時產量大於17件。通過第三四分位數23件，可以說明有3／4的工人時產量小於23件，有l／4的工人時產量大於23件。

　　如果n+1不是4的倍數， $Q 1$ 、 $Q 2$ 、 $Q 3$ 的位置便是小數。可按小數比例乘以前後兩項標誌值之差求出其數值。比如有20名工人，則n=20，其四分位數為：

　　 $Q 1$ 位置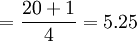 $=\frac{20+1}{4}=5.25$ ,則 $Q 1$ =17+(18-17)×0.25=17.25件；

　　 $Q 2$ 位置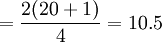 $=\frac{2(20+1)}{4}=10.5$ ，則 $Q 2$ ＝20+(21-20)×0.5=20.5件；

　　 $Q 3$ 位置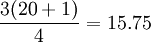 $\frac{3(20+1)}{4}=15.75$ ，則 $Q 3$ ＝23.75件。

　　如果根據組距數列計算四分位數，也應按從組距數列計算中位數的方法，首先確定其位置。這時 $Q 1$ 、 $Q 2$ 、 $Q 3$ 的位置應分別根據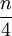 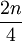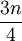$\frac{n}{4}$ 、 $\frac{2n}{4}$ 、 $\frac{3n}{4}$ 來確定。然後，再仿照求中位數的辦法，按比例推算其數值。

[編輯]

參考文獻

↑ 論四分位數的計算.作者:祁德軍,陳明
↑ 張六琥張躍慶主編.實用現代經濟管理辭典.國際文化出版公司,1989年06月第1版.

取自"https://wiki.mbalib.com/zh-tw/%E5%9B%9B%E5%88%86%E4%BD%8D%E6%95%B0"

打开MBA智库App, 阅读完整内容打开App

如果您認為本條目還有待完善，需要補充新內容或修改錯誤內容，請編輯條目或投訴舉報。

本条目由以下用户参与贡献

Zfj3000,连晓雾.

頁面分類: 統計術語

評論(共18條)

提示:評論內容為網友針對條目"四分位數"展開的討論，與本站觀點立場無關。

155.69.189.* 在 2009年1月6日 21:25 發表

能否舉個i不是整數的例子啊？

回複評論

119.123.45.* 在 2009年4月7日 11:05 發表

是啊，I 不是整數的話，應該如何計算呢，能否舉個例子。謝謝

回複評論

Angle Roh (討論 | 貢獻) 在 2009年4月7日 15:12 發表

已對條目內容進行補充

回複評論

123.120.16.* 在 2009年6月1日 09:06 發表

該四分位的演算法從一開始就是錯誤的。中位是在（n+1）/2的位置，四分位的位置是（中位位置+1）/2。所以（n+1）/4肯定不對！例如n=5時，下四分位是2。用Excel統計可以驗證結果。

回複評論

93.96.207.* 在 2009年9月7日 03:48 發表

155.69.189.* 在 2009年1月6日 21:25 發表

能否舉個i不是整數的例子啊？

就是咯~~

回複評論

203.91.44.* 在 2010年6月13日 11:47 發表

中位是在（n+1）/2的位置，下四分位的位置是（中位位置+1）/2。所以（n+3）/4才對！上四分位的位置是（中位位置+N）/2。所以（3n+1）/4才對！。用Excel統計可以驗證結果。

回複評論

222.246.109.* 在 2010年7月16日 23:17 發表

不錯

回複評論

119.98.65.* 在 2010年10月8日 20:32 發表

跟生物統計學教材上的不一樣

回複評論

59.38.33.* 在 2011年7月6日 11:21 發表

203.91.44.* 在 2010年6月13日 11:47 發表

此演算法才正確！

回複評論

117.43.126.* 在 2012年6月17日 17:26 發表

那個帶有小數的例子不對吧，可以用EXCEL驗證的

回複評論

219.142.28.* 在 2012年8月23日 08:55 發表

59.38.33.* 在 2011年7月6日 11:21 發表

此演算法才正確！

Q1=1+(n-1)/4=(n+3)/4; Q3=1+3(n-1)/4=(3n+1)/4.

回複評論

125.41.52.* 在 2013年1月17日 22:59 發表

最下麵那個舉例中的演算法怎麼和上面的都不一樣呢

回複評論

125.41.52.* 在 2013年1月17日 23:00 發表

最下麵四位數的舉例的演算法為什麼和上面的演算法不一致呢？

回複評論

111.76.20.* 在 2013年10月12日 12:17 發表

請問統計學中怎麼用四分位數判斷數據的分佈是右偏、左偏還是對稱啊

回複評論

58.71.139.* 在 2014年7月31日 23:36 發表

希望在上面可以先說清楚Q1.Q2.Q3是上四分位數,中位,還是下四分位數先明白比較快

回複評論

61.190.61.* 在 2015年3月15日 15:53 發表

117.43.126.* 在 2012年6月17日 17:26 發表

那個帶有小數的例子不對吧，可以用EXCEL驗證的

excel的QUARTILE函數四分位演算法是：Q1=(1n+3)/4，Q2=(2n+2)/2，Q3=(3n+1)/4,so...U C...

回複評論

140.136.31.* 在 2016年11月7日 16:28 發表

如果四分位數算完之後是3.12這樣的，就是小數部分比0.5小的，是進位還是捨去啊，比如3.12是第四位是四分位數還是第三位

回複評論

211.137.127.* 在 2019年1月2日 11:15 發表

如果只有兩個數據怎麼計算四分位數

回複評論

發表評論請文明上網，理性發言並遵守有關規定。

查看

工具▼

四分位數

出自 MBA智库百科(https://wiki.mbalib.com/)

目錄

什麼是四分位數

四分位數的計算^[1]

四分位數的案例分析

案例一^[2]

參考文獻

温馨提示

本条目相关课程

本条目由以下用户参与贡献

評論(共18條)

導航

意见反馈

查看

工具▼

四分位數

出自 MBA智库百科(https://wiki.mbalib.com/)

目錄

什麼是四分位數

四分位數的計算[1]

四分位數的案例分析

案例一[2]

參考文獻

温馨提示

本條目相關文檔

本条目相关课程

本条目由以下用户参与贡献

評論(共18條)

導航

意见反馈

四分位數的計算^[1]

案例一^[2]