描述性指标
出自 MBA智库百科(https://wiki.mbalib.com/)
目录 |
什么是描述性指标[1]
描述性指标是指反映社会现象实际情况的指标，如：城镇人口数、居民拥有电脑数、财政收入总额等等。
描述性指标的内容[2]
描述指标是用于反映社会经济现象总体客观状况，反映社会经济活动的条件、过程和结果的统计指标。例如，反映社会经济活动条件的指标，如各种自然资源拥有量指标、土地面积指标、劳动力资源指标、科技力量指标等等；反映社会经济活动过程和结果的指标，如社会总产值；国民收入、国民生产总值、固定资产、物资的增加量、减少量和库存量、进出口贸易额、利润额、财政收入与支出等等；反映社会物质文化生活状况的指标，如居民平均收入与支出、居民文化程度、在校学生数、医疗机构及床位数、文化娱乐设施等指标。这类指标提供对社会经济活动状况的基本认识，是统计信息的主体。
统计描述指标及其选用原则[3]
统计描述是统计分析的重要组成部分，是统计推断的基础，它是指用统计表和统计图或利用统计指标来描述资料的特征。
(一)数值变量的统计学描述
数值变量也叫做计量资料，是对观察对象的某个指标采用度(衡)量的方法进行检测所得到的资料。数值变量资料的统计描述主要包括以下几个方面。
1．频数表。包括频数又称频率，是指某一变量观察结果在某一特定数值(或数值范围内)出现的次数。将事物分类之后统计出来的各类频数排列成表格，即为频数表。利用频数分析，可从一大堆变量观测值中直观地了解变量的分布特征。
(1)频数表的编制方法。
1)求极差 找出观察值中的最大值和最小值，利用以下公式计算：
极差=最大值-最小值
2)确定组距和各组段的上下限 为了简化资料，显示数据的分布规律，对极差进行分割分组。适宜的分组数与观察值的个数的多少有关，一般观察值在30左右时，可分为5～6组，随观察值的增加，分组数可增加。组数一般为8～15组。
3)列表划记落在各组段内的观察值个数(频数)。
根据编制出的频数表即可了解该数值变量资料的频数分布特征。
(2)频数分布的特征及类型：
2)两种类型：对称分布和偏态分布，偏态分布又有正偏态和负偏态之分。
(3)频数表的用途：①描述资料的分布特征和分布类型。②为进一步计算有关指标或进行统计分析提供依据。③便于发现特大或特小的可疑值。④绘制频数分布图。
2．集中趋势的描述。描述一组观察值分布集中位置或平均水平的指标称为平均数。它能使人对资料有个简明概括的印象，并能进行资料问的比较。常用的平均数有算术平均数、几何均数和中位数。
(1)算术平均数。算术平均数简称均数，有总体平均数(μ)和样本平均数(
)之分，平均数描述一组数据在数量上的平均水平。样本均数的计算公式为：
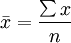
均数适用于表示对称分布，特别是正态分布的资料的、F均水平，不适用于偏态分布的资料。如有数据3、4、5、6、12，可见数据多在3～6之间，但均数为6，显然不能代表这组数据的中心位置，此时应用中位数描述其集中趋势。
(2)几何均数。几何均数适用于原始数据分布不对称，但经对数转换后呈对称分布的资料。这类资料可以是呈倍数关系的等比资料，如医学上血清抗体滴度资料。在应用中应注意观察值不能同时有正有负，同一资料算得的几何均数小于算术平均数。计算公式为：![G=\sqrt[n]{x_1x_2\ldots x_n}](/w/images/math/a/d/0/ad082e6a533d98962380e41e94c15caa.png)
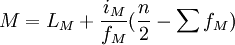
式中：LM为中位数所在组段的下限，iM为中位数所在组段的组距，fM为中位数所在组段的频数，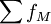
知为中位数所在组段的以前的累计频数。
中位数用于描述偏态分布资料的集中位置，它不受两端特大、特小值的影响，当分布末端无确切数据时也可计算。同时任何分布的定量数据均可用中位数描述其分布的集中趋势，适用范围较广。
3．离散程度的描述。集中趋势是数据分布的一个重要特征，但单有集中趋势指标还不能很好地描述数据的分布规律。为了比较全面地描述数据分布的规律，除了需要有描述集中趋势的指标外，还需引入描述数据分布离散程度的指标。描述离散趋势的指标有多种，最常用的有极差、四分位数间距、方差、标准差和变异系数。
(1)极差。又称全距，即最大和最小观察值之间的间距，用极差描述资料的离散程度简单明了，但它不能反映观察值的整个变异度，而且样本的例数越多，极差的可能就越大，因此用极差来描述离散趋势就不够稳定，易受奇异值的影响。
(2)四分位数间距。四分位数是特定的百分位数，其中P25为下四分位数Ql，P75为上四分位数Qu。四分位数间距即Qu − Ql。四分位数间距比极差稳定，是两个统计学点值之间的距离，但仍未考虑每个观察值的变异度。
(3)方差。离均差的绝对值之和或离均差平方和(SS)可用来描述资料的变异度。SS的均数(即均方)不受观察值个数的影响，用来描述资料的离散程度较离均差的绝对值之和或离均差平方和更好。方差也有总体方差和样本方差之分。样本方差的计算公式为：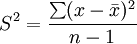
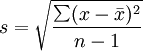
标准差可用于描述变量值的离散程度，与均数结合还可描述资料的分布情况，此外还可用于求参考值范围和计算标准差。
(5)变异系数。在比较多组资料的离散程度时，如这儿组资料的单位不同或均数相差悬殊时，用标准差就不合适。此时需要用到变异系数又称离散系数来比较，它实际上是标准差占均数的百分比例。计算公式为：
CV=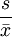
×100％
(二)分类变量的统计学描述
对分类变量资料进行统计描述的一般步骤，是先对观察测量得到的变量值(即观察值)进行分类汇总(即“计数”)得到分类资料频数表(属于绝对数指标)，再在此基础上计算相对数指标(即两个指标之比)才能对分类变量资料进行正确的描述。
1．常用的相对数指标。
(1)率：又称频率指标，用来说明某现象发生的频率或强度。计算公式为：
率=发生某现象的观察单位数÷可能发生某现象的观察单位总数×k
式中：k可为100％、万/万等。
如某居民区的年平均人口数为36 723人，经检查该区患急性传染病的人口数为433人，则某居民区该年急性传染病发病率为：117．9/万[(433/36 723)×(万/万)]。
(2)构成比：又称构成指标。其计算公式为：
构成比=某一组成部分的观察单位数÷同一事物个组成部分的观察单位总数×100％
构成比用来说明事物内部各组成部分所占比重或分布。如某市的急性传染病发病数为2 884人，其中有A居民区急性传染病发病数为545人，则该居民区占全市急性传染病发病数的比重为18．9％(545/2 884×100％)。事物内部各构成比之和必为1。
(3)比：又称相对比，为两个相对数之比。其基本计算公式为：比=A／B
说明A为B的若干倍或百分之几。A、B可为绝对数、相对数或平均数。如某市某年A区的急性传染病发病数为433人，B区的急性传染病发病数为541人，则B区与A区急性传染病发生数之比为1．25(541／433)。
2．应用相对数时应注意的问题。
(1)计算相对数时，分母不宜过小。
(2)构成比和率不能相互混淆。两者的区别如表1：
表1
| 构成比 | 率 | |
|---|---|---|
| 概念 | 说明事物内部组成部分所占比重或分布 | 说明某现象发生的频率或强度 |
| 合计 | 100％ | 分率不能直接相加 |
| 改变 | 任一部分比重的增减都会影响其他部分的比重 | 某一分率改变对其他分率无影响 |
(3)求平均数或总率时，分子、分母应分别相加，然后按相对数的计算公式重新计算。
(4)注意资料同质性、可比性。
(5)样本率或构成比的比较应建立在随机抽样的基础上，并作假设检验。
3．动态数列。
(1)概念：动态数列是一系列按时间顺序排列的统计指标(可以是绝对数、相对数或平均数)，用以说明事物在时间上的：变化和趋势。
(2)常用的分析指标：
1)绝对增长量，有累计年增长和逐年增长之分；
2)发展速度与增长速度，其中定基比描述变化趋势．环比用来描述指标的逐年波动情况；
3)平均发展速度和平均增长速度，其中平均发展速度是第n年指标除以基期指标的商再开n次方。
平均增长速度=平均发展速度-1(100％)
4．率的标准化。
(1)意义和基本思想：率的标准化可在比较总率时消除混杂因素(即内部构成不同)的影响，用标准化法将资料变换为符合可比条件。经常需要标化的指标有人口死亡率、病死率、发病率等，常见的混杂因素有年龄、病情等。
(2)标准率的计算步骤：
1)选取标准：常选用全世界、全国或本地区范围较大人群作为标准，此类标准最好。实践中也常用被标化组的合计作为标准。有时也会任选一组被标化组作为标准，但效果往往较差。
2)根据现有数据选用方法：
·直接法：已知标准人口数或标准人口年龄构成，被标化组需要知道各年龄组的率。以死亡率为例，当已知标准组的年龄别、人口数时，其计算公式为：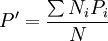
式中：P'为标准化率，Ni为标准组第i个年龄组的人口数，Pi为被标化组第i个年龄组的死亡率，N为标准组的总人数，
当已知标准组的年龄别、人口构成时，其计算公式为：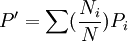
式中：P'为标准化率，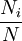
为标准组第i个年龄组的人口构成比，Pi为被标化组的死亡率。
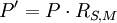
式中：P为标准组的总死亡率，RS,M为标化死亡比——是指被标化组实际死亡数与预期死亡数之比。
(3)应用注意事项：①标化率没有实际意义，仅作比较之用；②资料若为样本资料，则标化率的比较仍需假设检验；③当各年龄组的率有明显交叉时不宜采用标准化法。
