百分位数
出自 MBA智库百科(https://wiki.mbalib.com/)
百分位数(Percentile)
目录 |
百分位数又称百分位分数(percentile),是一种相对地位量数,它是次数分布中的一个点。把一个次数分布排序后,分为100个单位,百分位数就是次数分布中相对于某个特定百分点的原始分数,它表明在次数分布中特定个案百分比低于该分数。百分位数用P加下标m(特定百分点)表示。譬如,若P30等于60,则其表明在该次数分布中有30%的个案低于60分。
百分位数的应用[1]
百分位数用于描述一组数据某一百分位置的水平,多个百分位数结合应用,可全面描述一组观察值的分布特征;百分位数还可用于确定非正态分布资料的医学参考值范围。但应用百分位数时,样本含量要足够大,否则不宜取太靠近两端的百分位数。
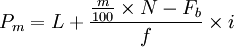
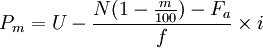
其中,Pm——第m百分位数;
L——Pm所在组的组实下限;
U——Pm所在组的组实上限;
f——Pm所在组的次数;
Fb——小于L的累积次数;
Fa——大于U的累积次数。
【例1】某省某年公务员考试考生分数分布如下表所示,预定取考分居前15%的考生进行面试选拔,请划定面试分数线。
| 分数分组 | 次数 | 向上累积次数 | 向下累积次数 | 向上累积相对次数 |
|---|---|---|---|---|
| 95~99 | 7 | 1640 | 7 | 100% |
| 90~94 | 16 | 1633 | 23 | 99.57% |
| 85~89 | 53 | 1617 | 76 | 98.60% |
| 80~84 | 78 | 1564 | 154 | 95.37% |
| 75~79 | 90 | 1486 | 244 | 90.61% |
| 70~74 | 119 | l396 | 363 | 85.12% |
| 65~69 | 159 | 1277 | 522 | 77.87% |
| 60~64 | 156 | 1118 | 678 | 68.17% |
| 55~59 | 140 | 962 | 818 | 58.66% |
| 50~54 | 145 | 822 | 963 | 50.12% |
| 45~49 | 140 | 677 | 1103 | 41.28% |
| 40~44 | 135 | 537 | 1238 | 32.74% |
| 35~39 | 130 | 402 | 1368 | 24.51% |
| 30~34 | 126 | 272 | 1494 | 16.59% |
| 25~29 | 78 | 146 | 1572 | 8.90% |
| 20~24 | 25 | 68 | 1597 | 4.15% |
| 15~19 | 20 | 43 | 1617 | 2.62% |
| 10~14 | 16 | 23 | 1633 | 1.40% |
| 5~9 | 7 | 7 | 1640 | 0.43% |
解:由于预定取考分居前15%的考生进行面试,即有85%的考生分数低于划定的分数线,由此可知,分数线在70~74这一组中。
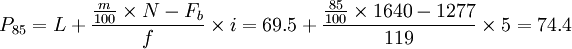
【例2】对于考试成绩的统计,如果您的成绩处在95的百分位数上,则意味着95%的参加考试者得到了和您一样的考分或还要低的考分,而不是您答对了95%的试题。也许您只答对了20%,即使如此,您取得的成绩也与95%的参加考试者一样好,或者比95%的参加考试者更好[2]。
【例3】假设想为退休存够钱。可创建一个包括所有不确定变量的模型,如投资年回报率、通货膨胀、退休时的开支等,得到概率分布的结果如下图所示,如果选择平均值,钱不够的概率就会有50%。所以选第90百分位数所对应的投资数,这样钱不够的概率将只有10%[2]。
- 徐文彬.第三节 百分位数与百分等级数 第四章 数据的离中趋势及其描述 教育统计学:思想、方法与应用.南京师范大学出版社,2007.3
评论(共17条)
到底是从大到小排列还是从小到大排列,刚开始说从大到小,举例又是从小到大的,看着晕!
应该是从小到大排列。
i=np%是啥意思呀 p50所对应的数据是不是就是均值呢?
添加和修改了部分内容,希望对你有帮助!~
计算中算出百分位数所在位置大于最大值,该怎么办? 如题 46,54,42,46,32的p97是多少?
应该不存在这个问题吧,你的题中只有五个数,m值不能设97,个案数是整数,要么20%40%之类的,应该是你算错了把!
已添加案例并附上参考文献,希望对您有帮助。
MBA智库百科是可以自由参与的百科,如有发现错误和不足,您也可以参与修改编辑,点击条目上方的编辑进入即可参与,期待您的加入!~
請問:如果班上共有50個學生,而其分數是100分的有20個,99分的20個,98分的有9個,97分的有1個,那麼求第97百分位數P97=?
我以例1为例来详细探讨一下。 首先要说明本词条中例1的解题计算是错误的! 其次不要被公式搞晕,公式是从概念中提炼出来的,理解了概念就明白了公式。反之,想从公式入手就比较抽象枯燥。
进入正题。 1.例1在现实应用中是什么意思呢? 其实就是1640个考生参加了公务员考试并取得有效成绩(最低分5分),如何计算出分数居考生总数前15%的考生的录取成绩呢? 也就是第85个百分位数的成绩,换句话说1640名考生中85%的人应当低于这个成绩。
2.理解表格的含义 1)分数分组(i,L,U) 考务人员将考试成绩按5分的差距(i)进行了分数分组,应该有100/5=20个组。 但是本例中显然去掉了最低一级“0~4”分这个组别,这是一个很好的例子。 一种可能是所有的考生都没有低于5分的,另一种可能是根本不考虑5分以下的。 在这列数据中包含了3个公式变量:i,L,U。 i:分数分组区间差; L:分数分组区间下限; U:分数分组区间上限。 这里有个重要问题要说明一下!每一个“分数分组”项中数据值的下限值就是该数据的值,而上限值应当是数值加1。 怎么理解这句话呢?以表中第二行记录“90~94”为例, 它代表的真正含义是90分(含)以上,95分(不含)以下成绩范围,而不是90~94分之间的成绩,否则94.5分往哪儿放? 忽略这一点,用第二个公式计算就无法得到正确的答案。
2)次数 (f,N) 次数即统计次数(f),在本例中可以理解为对应分数段的统计人数。 第一行数据表示95分(含)以上的考生一共7人; 第二行数据表示90分(含)以上、95分(不含)以下的考生一共为16人,以此类推。 所有各行次数累计的总和N,也就是统计总数。 本例中所有次数的总和N为1640人。
3)向上累积次数(Fb) 即从低分数段向高分数段依次将对应次数进行累加。 10分以下的7人;15分以下的7+16=23人;20分以下的23+20=43人......
4)向下累积次数(Fa) 即从高分数段向低分数段依次将对应次数进行累加。 95分以上的7人;90分以上的7+16=23人;85分以上的23+53=76人......
5)向上累积相对次数(m%) 即“向上累积次数”与总人数N的百分比,也就是百分位数。 例第四行数据“95.37%”的含义是:1564名考试成绩在85分以下,占全部1640名考生的95.37% 第六行的意思是85.12百分位数的考生成绩在75分以下,共有1396人。
3.如何计算 1)首先以例题中取前15%的考生为例进行计算。 两个公式都可以用,先以第一个公式进行计算。 前15%也就是找到第85(m)个百分位数,表格第五列中并没有85%这个数, 但是我们能够找到包含85%——第六行的“85.12%”,也就是寻找第一个大于85%的数据。 (如果我们想录取前5%的考生,找到的对应数据就是第四行的“95.37%”。) 那么在70分(L)和75分(U)之间我们到底要取多少分才能保证刷掉的人数正好占总人数的85%呢? 计算: a)总人数1640的85%是1394人;(m/100*N) b)70分以下的是1277人,1394-1277=117人。也就是从70~75分之间的这119人中还要刷掉117人。(m/100*N-Fb) c)这117人与该区间总人数119人的对应比重的分值=117/119*5=4.92。((m/100*N-Fb)/f*i) d)第85个百分位数对应分数=70+4.92=74.92分。(L+(m/100*N-Fb)/f*i) e)正确答案为录取成绩为74.92分。 用公式二进行检验: U=75,N=1640,m=85,Fa=244,f=119,i=5 P75=75-(1640*(1-85/100)-244)/119*5=74.92
2)假如我们只录取前5%的考生,即计算出第95个百分位所对应的成绩。 找到第四行数据,获得L=80, m=95, N=1640, Fb=1486, f=78, i=5 P95=80+(95/100*1640-1486)/78*5=84.62
4.补充说明 其实我们计算出来的数值只是参考数值。如本例录取前15%成绩的246人中,244人肯定高于录取成绩74.92分,另外2人是否能达到这个成绩就不好说。 这也从另一个侧面说明了i取值大小的意义了。取值越大计算误差越大,但是统计工作量越小;取值越小则反之。
請問:如果班上共有50個學生,而其分數是100分的有20個,99分的20個,98分的有9個,97分的有1個,那麼求第97百分位數P97=?
你这个例子比较极端,不过按照你的题目计算 P97=99.5+(97%*50-30)/20*0.5=99.96
i=np%是啥意思呀 p50所对应的数据是不是就是均值呢?
50%的是中位数,怎么会是均值呢!他们不一定相等








到底是从大到小排列还是从小到大排列,刚开始说从大到小,举例又是从小到大的,看着晕!