正態分佈
出自 MBA智库百科(https://wiki.mbalib.com/)
正態分佈(Normal distribution),也稱高斯分佈(Gaussian distribution)
目錄 |
正態分佈是一種概率分佈。正態分佈是具有兩個參數μ和σ2的連續型隨機變數的分佈,第一參數μ是遵從正態分佈的隨機變數的均值,第二個參數σ2是此隨機變數的方差,所以正態分佈記作N(μ,σ2 )。遵從正態分佈的隨機變數的概率規律為取 μ鄰近的值的概率大 ,而取離μ越遠的值的概率越小;σ越小,分佈越集中在μ附近,σ越大,分佈越分散。正態分佈的密度函數的特點是:關於μ對稱,在μ處達到最大值,在正(負)無窮遠處取值為0,在μ±σ處有拐點。它的形狀是中間高兩邊低 ,圖像是一條位於x 軸上方的鐘形曲線。當μ=0,σ2 =1時,稱為標準正態分佈,記為N(0,1)。μ維隨機向量具有類似的概率規律時,稱此隨機向量遵從多維正態分佈。多元正態分佈有很好的性質,例如,多元正態分佈的邊緣分佈仍為正態分佈,它經任何線性變換得到的隨機向量仍為多維正態分佈,特別它的線性組合為一元正態分佈。
正態分佈是最重要的一種概率分佈。正態分佈概念是由德國的數學家和天文學家Moivre於1733年首次提出的,但由於德國數學家Gauss率先將其應用於天文學家研究,故正態分佈又叫高斯分佈。高斯這項工作對後世的影響極大,他使正態分佈同時有了“高斯分佈”的名稱,後世之所以多將最小二乘法的發明權歸之於他,也是出於這一工作。高斯是一個偉大的數學家,重要的貢獻不勝枚舉。但現今德國10馬克的印有高斯頭像的鈔票,其上還印有正態分佈的密度曲線。這傳達了一種想法:在高斯的一切科學貢獻中,其對人類文明影響最大者,就是這一項。在高斯剛作出這個發現之初,也許人們還只能從其理論的簡化上來評價其優越性,其全部影響還不能充分看出來。這要到20世紀正態小樣本理論充分發展起來以後。皮埃爾-西蒙·拉普拉斯很快得知高斯的工作,並馬上將其與他發現的中心極限定理聯繫起來,為此,他在即將發表的一篇文章(發表於1810年)上加上了一點補充,指出如若誤差可看成許多量的疊加,根據他的中心極限定理,誤差理應有高斯分佈。這是歷史上第一次提到所謂“元誤差學說”——誤差是由大量的、由種種原因產生的元誤差疊加而成。後來到1837年,海根(G.Hagen)在一篇論文中正式提出了這個學說。
其實,他提出的形式有相當大的局限性:海根把誤差設想成個數很多的、獨立同分佈的“元誤差” 之和,每隻取兩值,其概率都是1/2,由此出發,按狄莫佛的中心極限定理,立即就得出誤差(近似地)服從正態分佈。皮埃爾-西蒙·拉普拉斯所指出的這一點有重大的意義,在於他給誤差的正態理論一個更自然合理、更令人信服的解釋。因為,高斯的說法有一點迴圈論證的氣味:由於算術平均是優良的,推出誤差必須服從正態分佈;反過來,由後一結論又推出算術平均及最小二乘估計的優良性,故必須認定這二者之一(算術平均的優良性,誤差的正態性) 為出發點。但算術平均到底並沒有自行成立的理由,以它作為理論中一個預設的出發點,終覺有其不足之處。拉普拉斯的理把這斷裂的一環連接起來,使之成為一個和諧的整體,實有著極重大的意義。
1、集中性:正態曲線的高峰位於正中央,即均數所在的位置。
2、對稱性:正態曲線以均數為中心,左右對稱,曲線兩端永遠不與橫軸相交。
3、均勻變動性:正態曲線由均數所在處開始,分別向左右兩側逐漸均勻下降。
4、正態分佈有兩個參數,即均數μ和標準差σ,可記作N(μ,σ):均數μ決定正態曲線的中心位置;標準差σ決定正態曲線的陡峭或扁平程度。σ越小,曲線越陡峭;σ越大,曲線越扁平。
5、u變換:為了便於描述和應用,常將正態變數作數據轉換。
1.估計正態分佈資料的頻數分佈
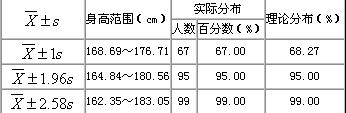
例1.某地1993年抽樣調查了100名18歲男大學生身高(cm),其均數=172.70cm,標準差s=4.01cm,
①估計該地18歲男大學生身高在168cm以下者占該地18歲男大學生總數的百分數;
②分別求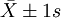 、
、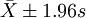 、
、 範圍內18歲男大學生占該地18歲男大學生總數的實際百分數,並與理論百分數比較。
範圍內18歲男大學生占該地18歲男大學生總數的實際百分數,並與理論百分數比較。
本例,μ、σ未知但樣本含量n較大,按式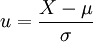 用樣本均數
用樣本均數 和標準差S分別代替μ和σ,求得u值,u=(168-172.70)/4.01=-1.17。查附表標準正態曲線下的面積,在表的左側找到-1.1,表的上方找到0.07,兩者相交處為0.1210=12.10%。該地18歲男大學生身高在168cm以下者,約占總數12.10%。其它計算結果見表-1。
和標準差S分別代替μ和σ,求得u值,u=(168-172.70)/4.01=-1.17。查附表標準正態曲線下的面積,在表的左側找到-1.1,表的上方找到0.07,兩者相交處為0.1210=12.10%。該地18歲男大學生身高在168cm以下者,約占總數12.10%。其它計算結果見表-1。
表-1:1100名18歲男大學生身高的實際分佈與理論分佈
2.制定醫學參考值範圍:亦稱醫學正常值範圍。它是指所謂“正常人”的解剖、生理、生化等指標的波動範圍。制定正常值範圍時,首先要確定一批樣本含量足夠大的 “正常人”,所謂“正常人”不是指“健康人”,而是指排除了影響所研究指標的疾病和有關因素的同質人群;其次需根據研究目的和使用要求選定適當的百分界值,如80%,90%,95%和99%,常用95%;根據指標的實際用途確定單側或雙側界值,如白細胞計數過高過低皆屬不正常須確定雙側界值,又如肝功中轉氨酶過高屬不正常須確定單側上界,肺活量過低屬不正常須確定單側下界。另外,還要根據資料的分佈特點,選用恰當的計算方法。常用方法有:
(1)正態分佈法:適用於正態或近似正態分佈的資料。
雙側界值: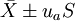 單側上界:
單側上界: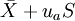 ,或單側下界:
,或單側下界: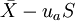
(2)對數正態分佈法:適用於對數正態分佈資料。
雙側界值: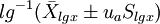 ;單側上界:
;單側上界: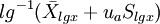 ,或單側下界:
,或單側下界: 。
。
常用u值可根據要求由表-2查出。
(3)百分位數法:常用於偏態分佈資料以及資料中一端或兩端無確切數值的資料。
雙側界值:P2.5和P97.5;單側上界:P95,或單側下界:P5。
表-2:常用u值表
參考值範圍(%) 單側 雙側 80 0.842 1.282 90 1.282 1.645 95 1.645 1.960 99 2.326 2.576
3.正態分佈是許多統計方法的理論基礎:如t分佈、F分佈、x2分佈都是在正態分佈的基礎上推導出來的,u檢驗也是以正態分佈為基礎的。此外,t分佈、二項分佈、Poisson分佈的極限為正態分佈,在一定條件下,可以按正態分佈原理來處理。
數據正態分佈檢驗 Q-Q圖[1]
要觀察某一屬性的一組數據是否符合正態分佈,可以有兩種方法(目前我知道這兩種,並且這兩種方法只是直觀觀察,不是定量的正態分佈檢驗):
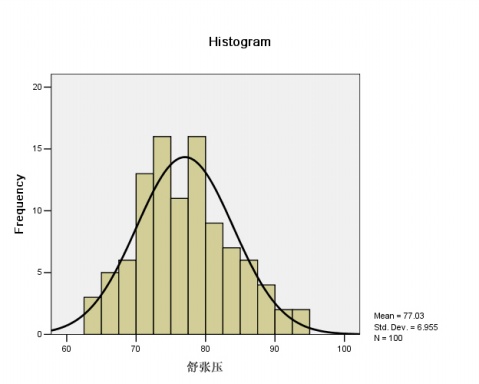
1:在spss(Statistical Package for the Social Sciences,即“社會科學統計軟體包”)里的基本統計分析功能里的頻數統計功能里有對某個變數各個觀測值的頻數直方圖中可以選擇繪製正態曲線。具體如下:Analyze-----Descriptive Statistics-----Frequencies,打開頻數統計對話框,在Statistics里可以選擇獲得各種描述性的統計量,如:均值、方差、分位數、峰度、標準差等各種描述性統計量。在Charts里可以選擇顯示的圖形類型,其中Histograms選項為柱狀圖也就是我們說的直方圖,同時可以選擇是否繪製該組數據的正態曲線(With norma curve),這樣我們可以直觀觀察該組數據是否大致符合正態分佈。如下圖:
從上圖中可以看出,該組數據基本符合正態分佈。
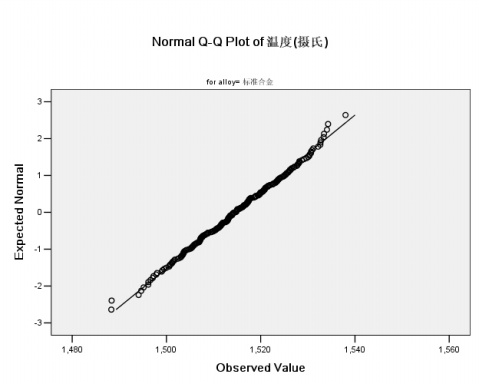
2:正態分佈的Q-Q圖:在spss里的基本統計分析功能里的探索性分析裡面可以通過觀察數據的q-q圖來判斷數據是否服從正態分佈。
具體步驟如下:Analyze-----Descriptive Statistics-----Explore打開對話框,選擇Plots選項,選擇Normality plots with tests選項,可以繪製該組數據的q-q圖。圖的橫坐標為改變數的觀測值,縱坐標為分位數。若該組數據服從正態分佈,則圖中的點應該靠近圖中直線。
縱坐標為分位數,是根據分佈函數公式F(x)=i/n+1得出的.i為把一組數從小到大排序後第i個數據的位置,n為樣本容量。若該數組服從正態分佈則其q-q圖應該與理論的q-q圖(也就是圖中的直線)基本符合。對於理論的標準正態分佈,其q-q圖為y=x直線。非標準正態分佈的斜率為樣本標準差,截距為樣本均值。
如下圖:








如何證明一組數據是符合正態分佈的?