泊松分佈
出自 MBA智库百科(https://wiki.mbalib.com/)
泊松分佈(Poisson Distribution)
目錄 |
Poisson分佈(法語:loi de Poisson,英語:Poisson distribution,譯名有泊松分佈、普阿松分佈、卜瓦松分佈、布瓦松分佈、布阿松分佈、波以松分佈、卜氏分配等),是一種統計與概率學里常見到的離散機率分佈(discrete probability distribution),由法國數學家西莫恩·德尼·泊松(Siméon-Denis Poisson)在1838年時發表。
泊松分佈(Poisson distribution),台譯卜瓦松分佈(法語:loi de Poisson,英語:Poisson distribution,譯名有泊松分佈、普阿松分佈、卜瓦松分佈、布瓦松分佈、布阿松分佈、波以松分佈、卜氏分配等),是一種統計與概率學里常見到的離散機率分佈(discrete probability distribution)。泊松分佈是以18~19 世紀的法國數學家西莫恩·德尼·泊松(Siméon-Denis Poisson)命名的,他在1838年時發表。這個分佈在更早些時候由貝努里家族的一個人描述過。
泊松分佈的概率質量函數為:
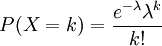
泊松分佈的參數λ是單位時間(或單位面積)內隨機事件的平均發生率。
泊松分佈適合於描述單位時間內隨機事件發生的次數。如某一服務設施在一定時間內到達的人數,電話交換機接到呼叫的次數,汽車站臺的候客人數,機器出現的故障數,自然災害發生的次數等等。
若隨機變數X取0和一切正整數值,在n次獨立試驗中出現的次數x恰為k次的概率P(X=k)=(k=0,1,...,n),式中λ是一個大於0的參數,此概率分佈稱為泊松分佈。它的期望值為E(x)=λ,方差為D(x) = λ。當n很大,且在一次試驗中出現的概率P很小時,泊松分佈近似二項分佈。
Poisson分佈主要用於描述在單位時間(空間)中稀有事件的發生數. 即需滿足以下四個條件:[1]
1、給定區域內的特定事件產生的次數,可以是根據時間,長度,面積來定義;
2、各段相等區域內的特定事件產生的概率是一樣的;
3、各區域內,事件發生的概率是相互獨立的;
4、當給定區域變得非常小時,兩次以上事件發生的概率趨向於0。
例如:
1、放射性物質在單位時間內的放射次數;
2、在單位容積充分搖勻的水中的細菌數;
3、野外單位空間中的某種昆蟲數等。
由泊松分佈知E[N(t) − N(t0)] = D[N(t) − N(t0)] = λ(t − t0)
特別的,令t_0=0.由於假設N(0)=0,故可推知泊松過程的均值函數和方差函數分別為E[N(t)] = λt,D[N(t)] = λt,
泊松過程的強度\lambda (常數)等於單位長時間間隔內出現的質點數目的期望值。即對泊松分佈有:E(X) = D(X) = λ
1、泊松分佈是一種描述和分析稀有事件的概率分佈。要觀察到這類事件,樣本含量n必須很大。
2、λ是泊松分佈所依賴的唯一參數。λ值愈小,分佈愈偏倚,隨著λ的增大,分佈趨於對稱。
3、當λ = 20時,分佈泊松接近於正態分佈;當λ = 50時,可以認為泊松分佈呈正態分佈。在實際工作中,當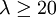 時就可以用正態分佈來近似地處理泊松分佈的問題。
時就可以用正態分佈來近似地處理泊松分佈的問題。
- ↑ 戴維 M. 萊文等.《以EXCEL為決策工具的商務統計》.機械工業出版社,2009








好,謝謝分享!