隨機事件
出自 MBA智库百科(https://wiki.mbalib.com/)
隨機事件(Random Event)
目錄 |
隨機事件是指在一定條件下可能發生也可能不發生的事件。應該註意的是,事件的結果是相應於"一定條件"而言的。因此,要弄清某一隨機事件,就必須明確何為事件發生的條件,何為在此條件下產生的結果。
例如,某人作試驗"向上拋擲一枚質地均勻的硬幣","質地均勻的硬幣"是條件,在此條件下,硬幣落地時正面向上(或反面向上)則是結果;又如,某氣象臺每天中午觀察風速,則時間、地點是條件,觀察到的風速是結果。
- 結果的隨機性。即在相同的條件下做重覆的試驗時,如果試驗的結果不止一個,則在試驗前無法預料哪一種結果將發生.
隨機事件在一次試驗中是否發生雖然不能事先確定,但是在大量重覆試驗的情況下,它的發生呈現出一定的規律性.
比如拋擲硬幣的次數很多時,出現正面的頻率值是穩定的,接近於0.5,在它附近擺動.
一般地,在大量重覆進行同一試驗時,事件A發生的頻率\frac{m}{n}總是接近於某個常數,在它附近擺動,這時就把這個常數叫做事件A的概率,記作P(A).
概率從數量上反映了一個事件發生的可能性的大小。概率的定義,實際也是求一個事件的概率的基本方法。記隨機事件A在n次試驗中發生了m次,那麼有:
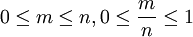 ,
,
於是可得 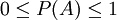
【例1】某人有5把鑰匙,但忘記了開房門的是哪一把,於是,他逐把不重覆地試開,問:
(1)恰好第三次打開房門所的概率是多少?
(2)三次內打開的概率是多少?
(3)如果5把內有2把房門鑰匙,那麼三次內打開的概率是多少?
解 5把鑰匙,逐把試開有 種結果,由於該人忘記了開房間的是哪一把,因此這些結果是等可能的。
(1)第三次打開房門的結果有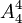 種,故第三次打開房門鎖的概率
種,故第三次打開房門鎖的概率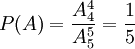
(2)三次內打開房門的結果有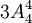 種,因此所求概率
種,因此所求概率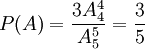
(3)方法1 因5把內有2把房門鑰匙,故三次內打不開的結果有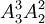 種,從而三次內打開的結果有
種,從而三次內打開的結果有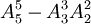 種,從而三次內打開的結果有
種,從而三次內打開的結果有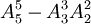 種,所求概率P(A)=\frac{A_5^5 - A_3^3 A_2^2}{A_5^5}=\frac{9}{10}.
種,所求概率P(A)=\frac{A_5^5 - A_3^3 A_2^2}{A_5^5}=\frac{9}{10}.
方法2 三次內打開的結果包括:三次內恰有一次打開的結果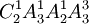 種;三次內恰有兩次打開的結果
種;三次內恰有兩次打開的結果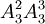 種.因此,三次內打開的結果有
種.因此,三次內打開的結果有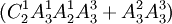 種,所求概率
種,所求概率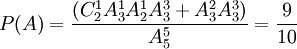
【例2】 某商業銀行為儲戶提供的密碼有0,1,2,…,9中的6個數字組成.
(1)某人隨意按下6個數字,按對自己的儲蓄卡的密碼的概率是多少?
(2)某人忘記了自己儲蓄卡的第6位數字,隨意按下一個數字進行試驗,按對自己的密碼的概率是多少?
解:(1)儲蓄卡上的數字是可以重覆的,每一個6位密碼上的每一個數字都有0,1,2,…,9這10種,正確的結果有1種,其概率為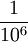 ,隨意按下6個數字相當於隨意按下106個,隨意按下6個數字相當於隨意按下106個密碼之一,其概率是
,隨意按下6個數字相當於隨意按下106個,隨意按下6個數字相當於隨意按下106個密碼之一,其概率是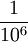 .
.
(2)以該人記憶自己的儲蓄卡上的密碼在前5個正確的前提下,隨意按下一個數字,等可能性的結果為0,1,2,…,9這10種,正確的結果有1種,其概率為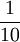 .
.








學歷太淺