互斥事件
出自 MBA智库百科(https://wiki.mbalib.com/)
互斥事件(Exclusive Event)
目錄 |
互斥事件是指在某一試驗中不可能同時發生的事件。事件A和B的交集為空,A與B就是互斥事件,也叫互不相容事件。也可敘述為:不可能同時發生的事件。如A∩B為不可能事件(A∩B=Φ),那麼稱事件A與事件B互斥,其含義是:事件A與事件B在任何一次試驗中不會同時發生。
互斥事件是指事件A與事件B在一次試驗中不會同時發生,其具體包括三種不同的情形:(1)事件A發生且事件B不發生;(2)事件A不發生且事件B發生;(3)事件A與事件B同時不發生,而對立事件是指事件A 與事件B有且僅有一個發生,其包括兩種情形;(1)事件A發生B不發生;(2)事件B發生事件A不發生,對立事件是互斥事件的特殊情形.
“互斥事件”與“相互獨立事件”是兩個不同的概念,二者不能混淆。
兩個事件互斥是指兩個事件不可能同時發生,兩個事相互獨立是指一個事件的發生與否對另一個事件發生的概率沒有影響。它們雖然都描繪了兩個事件間的關係,但所描繪的關係是根本不同的。
若A、B互斥,且P(A)>0 ,P(B)>0,則它們不可能互相獨立,因為A發生的條件下,B不可能發生,即 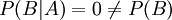 ,所以A、B不是互相獨立。
,所以A、B不是互相獨立。
互斥事件有一個發生的概率
【例1】
房間里有6個人,求至少有2個人的生日在同一月內的概率.
解 6個人生日都不在同一月內的概率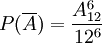 .故所求概率為
.故所求概率為 .
.
【例2】[1]
從一副52張的撲克牌中任取4張,求其中至少有兩張牌的花色相同的概率。
解法1 任取四張牌,設至少有兩張牌的花色相同為事件A;四張牌是同一花色為事件B1;有3張牌是同一花色,另一張牌是其他花色為事件B2;每兩張牌是同一花色為事件B3;只有兩張牌是同一花色,另兩張牌分別是不同花色為事件B4,可見,B1,B2,B3,B4彼此互斥,且A = B1 + B2 + B3 + B4。
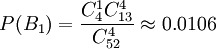 ,
, 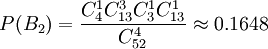 ,
,
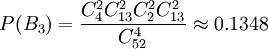 ,
, 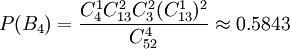 ,
,
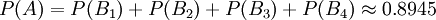
解法2 設任取四長牌中至少有兩張牌的花色相同為事件A,則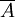 為取出的四張牌的花色各不相同,
為取出的四張牌的花色各不相同,
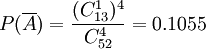
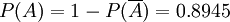
答:至少有兩張牌花色相同的概率是0.8945
【例3】[2]
在20件產品中有15件正品,5件次品,從中任取3件,求:(1)恰有1件次品的概率;(2)至少有1件次品的概率.
解
(1)從20件產品中任取3件的取法有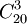 ,其中恰有1件次品的取法為
,其中恰有1件次品的取法為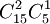 。
。
恰有一件次品的概率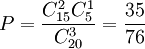 .
.
(2)解法一 從20件產品中任取3件,其中恰有1件次品為事件A1,恰有2件次品為事件A2,3件全是次品為事件A3,則它們的概率
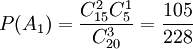 ,
, 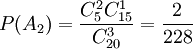 ,
, 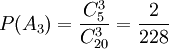 ,
,
而事件A1、A2、A3彼此互斥,因此3件中至少有1件次品的概率
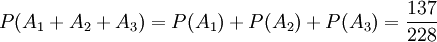
解法二 記從20件產品中任取3件,3件全是正品為事件A,那麼任取3件,至少有1件次品為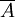 ,根據對立事件的概率加法公式
,根據對立事件的概率加法公式








有點難理解,能再通熟一點嗎?