巴恰塔亞模型
出自 MBA智库百科(https://wiki.mbalib.com/)
目錄 |
巴恰塔亞模型概述[1]
1979年，巴恰塔亞將其1977年在麻省理工學院所作的博士論文中的一章整理後發表在《貝爾經濟學刊》上。在文中，他構建了一個與羅斯模型非常相近的股利信號模型。但事後證明，巴恰塔亞模型可稱為與利蘭-派爾模型、羅斯模型和米勒-洛克模型齊名的信號模型，在股利政策的研究理論中占有重要的地位。巴恰塔亞認為，在不完美情況下，現金股利具有的信息內容，是未來預期盈利的事前信號。
巴恰塔亞模型的內容[1]
巴恰塔亞模型假設：
(2)現有資產產生的所有現金流量都可以理性地再投資；
(3)股利決策是由內部管理者做出的，由於其獎金與股東財富相聯繫，所以內部管理者的經營目標是股東財富最大化；
(4)只有內部管理者惟一知道現金流量分佈信息；
(5)風險中性；
(6)期限為一年。
用X表示從新項目所獲得的不確定性的現金流量，現金股利的個人所得稅率為1 − α，資本利得不徵稅，D表示新增發的股利，V(D)表示因新增股利而增加的清算價值。
如果X > D，則現有股東將獲得稅後股利αD，企業再投資需要從外部籌集的資金減少(X − D)元。
如果X < D如，企業支付的股利仍為D，資金不足部分(D—x)將給現有股東帶來(1 + β)(D − X)的成本。所以，現有股東的新增價值函數為:
![E(D)=\frac{1}{1+r}\left[ V(D)+\alpha D+\int_D^{\overline{X}}(X-D)f(X)dX+\int_{\underline {X}}^D(1+\beta)(X-D)f(X)dX \right]](/w/images/math/a/a/e/aae542c01da6823f2464b5ba04301849.png)
![=frac{1}{1+r}\left[ V(D)+M-(1-\alpha)D-\beta \int_{\underline {X}}^D F(X)dX \right]](/w/images/math/d/3/2/d320371fd45c718723f4c271e14e1c82.png)
……(1)
式中：f(X)和F(X)為X在區問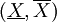
的密度函數和分佈函數；M為現金流量的平均值；r為貼現率。
假設投資項目的現金流量分佈在[0,t]，平均值為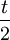
，各個企業的t大小不同，最小值為tmin，最大值為tmax，但是投資者無法區分t的大小。為此，作為企業股東的代理人，管理者通過股利支付決策向外發射信號幫助投資者區分t，並使自己的報酬最大化，即:
![max E(D)=max \left\{ \frac{1}{1+r}\left[ \frac{t}{2}+V(D)-(1-\alpha)D-\beta \frac{D^2}{2t} \right] \right \}](/w/images/math/1/b/f/1bf04fd1628f5db32d2b3a8c82f1e50f.png)
……(2)
求導，得:
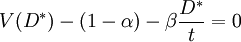……（3）
巴恰塔亞認為，只有當預期現金流量實現了，即V(D)與股利信號顯示的價值一致時，才能達到均衡。相對於資本利得來講，股利傳遞信息的價值是確定的，而且它可以用來抵消股利所得的稅收損失，從而即使管理層控制權力很大的公司也樂於支付股利，因為只有當股利分配方案向外界披露後，該信息引起的公司價值增值才能夠為現有的股東所獲得。
