米勒-羅克模型

出自 MBA智库百科(https://wiki.mbalib.com/)

　　米勒和洛克1985年依據“凈股利”的概念建立了一個財務信息傳遞模型，首次將股利分配和外部融資結合起來，模型假設管理者為使在股利消息發佈日到公司實際財務報告公佈之前賣出股票的投資者獲得較高的收益，會提高股利支付水平，犧牲一些計劃的投資機會。由於已減少投資水平的信息市場並不知道，因此股利信息傳導了有關公司未來發展比實際更好的錯誤信息使股價上漲。當市場充分認識到內部人靠犧牲投資這一代價來換取高股利這一行為的動機，會形成一個均衡的股利水平。

　　假設未來盈利取決於當期投資，那麼，可以認為凈經營收入等於由投資額確定的函數與隨機誤差之和，即有：

　　NOI₁ = f(I₀) + ε₁

　　NOI₂ = f(I₁) + ε₂

　　式中：ε₁和ε₂是均值為零的隨機誤差項。又假定E(ε₁ / ε₂) = γε₁，如果將γ(0 < γ < 1)解釋為持續繫數，則可以認為市場根據磨擦信息(第1期的誤差)部分地進行調整。如果用E₀。來表示當期的公司價值決定於股利宣告前的信息，則當期股東財富的期望值為:

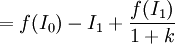　　　　（1）

　　相應地，股利宣告後的公司價值為:

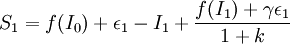　　　　（2）

　　式(2)減去式(1)，可得到股利宣告的影響為:

　　上式表明，股利宣告對股東財富的影響取決於“意外的利潤變化”。因此，我們可以預測利潤的意外變化對股利宣告目的股價變化是相互關聯的。利潤的意外變化和凈股利的意外變化可以傳播同樣的信息。股利的突然增加將使股東財富隨之增加，意外的新股發行或新債發行則被視為公司未來發展前景不佳的信息。

　　米勒-洛克模型說明，公司管理層為了傳遞公司業績必須採取相對較高的股利支付策略，結果向市場傳遞錯誤的信息，誘使股價升高，給立即出售股票的投資者帶來的好處，但欺騙了購入股票的投資者。然而在現實中一般管理層是不會接受米勒和洛克提出的顯示均衡策略，如果公司管理層經常接受一策略，不但很快會被新股東發覺，進而影響其權力的穩定和年薪水平，還會因為公司長期持續投資不足而成為市場收購兼併的主要目標。

• Bhattacharya模型
• 約翰-朗模型
• 約翰-威廉斯模型