米勒-罗克模型
出自 MBA智库百科(https://wiki.mbalib.com/)
目录 |
米勒-罗克模型概述[1]
米勒和洛克1985年依据“净股利”的概念建立了一个财务信息传递模型,首次将股利分配和外部融资结合起来,模型假设管理者为使在股利消息发布日到公司实际财务报告公布之前卖出股票的投资者获得较高的收益,会提高股利支付水平,牺牲一些计划的投资机会。由于已减少投资水平的信息市场并不知道,因此股利信息传导了有关公司未来发展比实际更好的错误信息使股价上涨。当市场充分认识到内部人靠牺牲投资这一代价来换取高股利这一行为的动机,会形成一个均衡的股利水平。
米勒-罗克模型内容[1]
假设未来盈利取决于当期投资,那么,可以认为净经营收入等于由投资额确定的函数与随机误差之和,即有:
NOI1 = f(I0) + ε1
NOI2 = f(I1) + ε2
式中:ε1和ε2是均值为零的随机误差项。又假定E(ε1 / ε2) = γε1,如果将γ(0 < γ < 1)解释为持续系数,则可以认为市场根据磨擦信息(第1期的误差)部分地进行调整。如果用E0。来表示当期的公司价值决定于股利宣告前的信息,则当期股东财富的期望值为:
![E(S_1)=S_0(NOI_1)-E_0(I_1)+\frac{E_0[f(I_1)]}{1+k}](/w/images/math/7/1/3/7139cca4834cc1b895b877431fbd46b7.png)
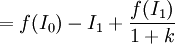 (1)
(1)
相应地,股利宣告后的公司价值为:
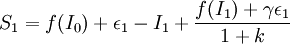 (2)
(2)
式(2)减去式(1),可得到股利宣告的影响为:
![S_1-E(S_1)=\epsilon_1[1+\frac{\gamma}{1+k}]](/w/images/math/b/9/f/b9f36e37d35ad96e4c8ed31290a87ccd.png)
![=[NOI_1-E_0(NOI_1)][1+\frac{\gamma}{1+k}]](/w/images/math/3/b/f/3bf5ecc4b8d87ae945c902cbd3b96642.png)
上式表明,股利宣告对股东财富的影响取决于“意外的利润变化”。因此,我们可以预测利润的意外变化对股利宣告目的股价变化是相互关联的。利润的意外变化和净股利的意外变化可以传播同样的信息。股利的突然增加将使股东财富随之增加,意外的新股发行或新债发行则被视为公司未来发展前景不佳的信息。
米勒-洛克模型说明,公司管理层为了传递公司业绩必须采取相对较高的股利支付策略,结果向市场传递错误的信息,诱使股价升高,给立即出售股票的投资者带来的好处,但欺骗了购入股票的投资者。然而在现实中一般管理层是不会接受米勒和洛克提出的显示均衡策略,如果公司管理层经常接受一策略,不但很快会被新股东发觉,进而影响其权力的稳定和年薪水平,还会因为公司长期持续投资不足而成为市场收购兼并的主要目标。







