貨幣先行模型
出自 MBA智库百科(https://wiki.mbalib.com/)
| 經濟分析工具 |
|---|
| [編輯] |
貨幣先行模型(Cash in advance model或CIA model)
目錄 |
當代西方巨集觀經濟學中另一廣泛使用的是貨幣先行(cash in advance或CIA)模型。該模型由克拉奧(Clower,1967)首先提出,其前提是消費必須用貨幣來購買。從技術上講,這相當於給模型增加了一個現金約束。克拉奧之後,大衛·斯托克曼(David Stockman,1981)發展了不僅消費品而且投資品也要用貨幣來購買的模型,羅伯特·盧卡斯(Robert E.Lucas)和斯道克曼(1983,1987)此後又將消費品分為必須用現金購買(現金物品)和可用信貸購買(信貸物品)的兩部分。CIA模型的優點在於它在保持動態最優分析的同時可以很容易地推導出貨幣需求。
該模型前提是消費必須使用貨幣來購買。為了達到這一目的,克拉奧在模型中假設了一個貨幣在先約束,即物品購買量受先前換取的貨幣量的約束。這是人們預算約束之外的另一約束。它隱含著兩種限制:其一,貨幣為購買物品的唯一媒介;其二,貨幣必須在物品交換之前換取。Clower之後,Stockman發展了不僅消費品而且投資品也要用貨幣來購買的模型。
不考慮不確定性,代表性行為人的目標函數可寫作:
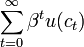 (1)
(1)
式中,β為貼現率,效用函數u(·)為連續可微、嚴格遞增的凹函數。行為人通過消費和資產選擇使目標函數極大化。為簡單起見,下麵我們不考慮資本,假定債券是除貨幣外的惟一金融資產。以名義量表示的該極大化問題的約束條件為:
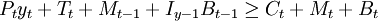 (2)
(2)
式中,Tt為來自於政府的凈轉移收入,Bt − 1是行為人在t—1期持有的t期到期的債券,It − 1是t—1到t期的名義債券收益,其他變數的含義相同。用t期物價水平去除上式,得到以實際量表示的約束:
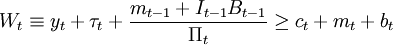 (3)
(3)
式中,τt = Tt / Pt,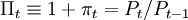 ,行為人在 t+1期的全部資源為:
,行為人在 t+1期的全部資源為:
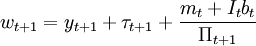 (4)
(4)
除了上述限制之外,CIA模型增加了1個貨幣先行約束:
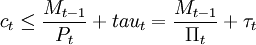 (5)
(5)
即t期的消費支出不能超過持有至t期的實際貨幣餘額加期初得到的轉移支付。由於持有貨幣存在放棄利率的機會成本,因此等式(5)通常取等號。
t期的選擇變數為cT,MT和Bt。由於行為人的消費既受資源限制也受現金約束,t期狀態可以用行為人所擁有的資源w和持有的現金mt − 1表示。
令值函數
V(wt,mt − 1) = maxu(ct) + βV(wt + 1,mt) (6)
則該值函數的極值約束於等式(3)、(4)和(5)。
令債券的實際收益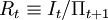 ,並且由等式(3)可知bt = wt − ct − mt,將這些關係代人等式(4),我們得到
,並且由等式(3)可知bt = wt − ct − mt,將這些關係代人等式(4),我們得到
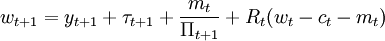
利用wt + 1這一表達式,令μ為與等式(5)相關的拉格郎日乘數,行為人的消費和貨幣持有量的一階條件為:
uc(ct) − βRtVw(wt + 1,mt) − μt = 0 (7)
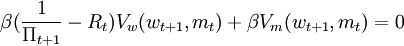 (8)
(8)
根據包絡定理:
Vw(wt,mt − 1) = βRtVw(wt + 1,mt) (9)
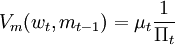 (10)
(10)
令λt,為時期t財富的邊際價值: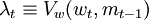 ,根據等式(9),等式(7)可寫作:
,根據等式(9),等式(7)可寫作:
uc(ct) = λt + μt (11)
即消費的邊際效用等於財富的邊際效用(λt)加貨幣提供的服務價值(μt)。由於消費品必須用貨幣來購買,因此與MIU模型相比,消費成本增加了貨幣提供的服務成本,行為人使消費的邊際效用等於該成本加財富的邊際效用。
CIA模型表明,如果貨幣供給為一常量,那麼貨幣在該模型中就具有正價值,這是因為貨幣能減少貨幣在先這一約束條件的影子成本。CIA模型的優點在於它保持動態最優分析的同時可以很容易地推導出貨幣需求。CIA模型與MIU模型一樣,它們並不專門討論為什麼貨幣具有如此特別的功能。但與MIU模型不一樣的是,CIA模型中關於貨幣的正價值並不依賴於任何關於消費和真實貨幣量在效用函數中的可分離性,這就讓模型擺脫了一個不必要的束縛。
CIA模型也說明瞭穩態的貨幣值為正和貨幣的超中性等問題。由於存在貨幣先行限制,實際消費等於實際貨幣餘額,穩態通脹率等於名義貨幣存量增長率。然而,基本的CIA模型不能說明通脹的福利成本和最優通貨膨脹率問題,根據這一模型,預期通脹不會影響貨幣需求,這一結論顯然不太現實。克拉奧之後,庫勒和阿爾文·漢森(Cooley and Alvin·Hansen,1989)將消費品進一步區分為現金物品和信貸物品,從而得以使消費與所持貨幣量之比隨預期通脹變動。







