影子成本

用手机看条目

出自 MBA智库百科(https://wiki.mbalib.com/)

影子成本(Shadow cost)

影子成本概述^[1]

　　考慮資源利用問題的線性規劃數學模型:

　　 $m a x Z = C X$

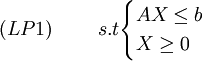
　　 $(LP1)\ \ \ \ \ \ \ s.t\begin{cases}AX \le b \\ X \ge 0 \end{cases}$

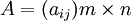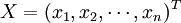　　其中 $C=(c_1,c_2,\cdots,c_n)$ 是效益繫數向量, $A=(a_{ij})m\times n$ 是產品對資源的消耗繫數矩陣, $b=(b_1,b_2,\cdots,b_m)^T$ 是資源限量向量, $X=(x_1,x_2,\cdots,x_n)^T$ 是決策變數向量。根據問題的實際意義,A,C,b中的元素均為非負元素。

　　設(LP1)的最優基為B,對應的最優解為 $X B = B - 1 b, X N = 0,$ 最優值 $m a x Z = C B B - 1 b$ 。其對偶線性規劃問題是:

　　 $m i n W = Y b$

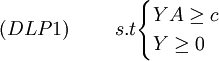
　　 $(DLP1)\ \ \ \ \ \ \ s.t\begin{cases}YA \ge c \\ Y \ge 0 \end{cases}$

　　其中 $Y=(y_1,y_2,\cdots,y_m)$ 。

　　如果某經濟系統利用n種原料生產符合m項質量指標(效用)要求的產品,m項質量指標(效用)的標準向量 $b=(b_1,b_2,\cdots,b_m)^T$ ,n種原料的單位成本為向量 $C=(c_1,c_2,\cdots,c_n)$ ,n種原料對m項質量指標含有量的繫數矩陣為

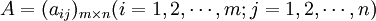
　　 $A=(a_{ij})_{m\times n}(i=1,2,\cdots,m;j=1,2,\cdots,n)$

　　那麼,選取n種原料的數量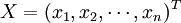 $X=(x_1,x_2,\cdots,x_n)^T$ 生產該產品,在達到質量指標要求的前提下,使S總成本達到最小。可以建立線性規劃數學模型:

　　 $m i n S = C X$

　　 $(LP2)\ \ \ \ \ \ \ s.t\begin{cases}AX \ge b \\ X \ge 0 \end{cases}$

　　其對偶線性規劃問題為:

　　 $m a x G = Y b$

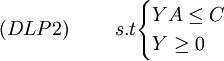
　　 $(DLP2)\ \ \ \ \ \ \ s.t\begin{cases}YA \le C \\ Y \ge 0 \end{cases}$

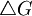　　其中 $Y=(y_1,y_2,\cdots,y_m)$ 。與影子價格的理論推導和經濟意義類似^[2],這裡對偶線性規劃問題(DLP2)的最優解可以解釋為線性規劃問題(LP2)中各種質量指標(效用)的邊際成本(marginal costs)或者稱為影子成本(shadow costs)。即在其他條件均不改變的情況下,改變第i種指標引起的總成本的改變數 $\triangle G$ 與第i種質量指標的改變數 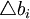$\triangle b_i$ 的比值

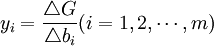
　　 $y_i=\frac{\triangle G}{\triangle b_i} (i=1,2,\cdots,m)$

　　影子成本的另一層含義是:如果降低某項質量指標(效用)的要求,產品的收益可能減少,影子成本就是經營者能夠接受的降低單位該項質量指標(效用)所減少的最大收益。

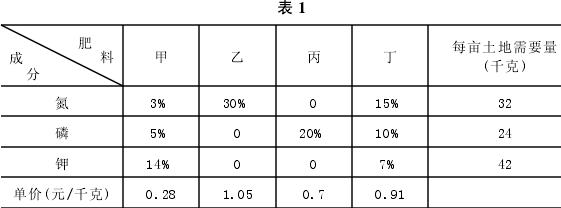
　　例如,在一塊土地上種植某種農作物,根據農作物生長和增產的需要,在其生長過程中每畝至少需要氮32千克、磷24千克、鉀42千克。現有四種複合肥料甲、乙、丙、丁,其每千克的購買價格及氮、磷、鉀含量(%)見表1。問該塊土地上每畝施這四種肥料各多少千克,才能既滿足農作物對氮磷鉀的需要,又使得施肥的總成本最低?

　　設每畝施肥甲、乙、丙、丁分別為 $x 1, x 2, x 3, x 4$ 千克,則可建立線性規劃數學模型:

　　 $m i n S = 0.28 x 1 + 1.05 x 2 + 0.7 x 3 + 0.91 x 4$

　　通過LINDO6.1(最優化求解軟體)對模型1進行求解,得: $x 1 = 480, x 2 = 58.67, x 3 = 0, x 4 = 0, m i n Z = 196$

　　即:每畝施肥料甲480千克,乙58.67千克,不施丙和丁,在滿足作物對氮磷鉀的需求的前提下,使得成本最小,最小成本為196元/畝。

　　如果從另一個角度思考問題,不購買複合肥而是購買單成分氮、磷、鉀的肥料,那麼氮、磷、鉀的價格應如何確定呢?或者說購買單成分氮、磷、鉀的肥料願意付出的價格是多少呢?

　　設每千克單成分氮、磷、鉀肥料的價格分別為 $y 1, y 2, y 3$ 元,則可以建立線性規劃模型:

　　 $m a x G = 32 y 1 + 24 y 2 + 42 y 3$

　　模型(DLP3)是(LP3)的對偶線性規劃問題。通過LINDO6.1對(DLP3)進行求解,得:

　　 $y 1 = 3.5, y 2 = 3.5, y 3 = 0, m a x G = 196$ 元

　　根據LINDO6.1對模型1的求解報告,氮磷鉀三種要素的對偶價格(dual price)分別為-3.5元,-3.5元和0。其實,對偶價格就是(LP3)的對偶線性規劃問題(DLP3)的最優解 $y 1, y 2, y 3$ 的相反數。這裡的對偶價格可以理解為在其他條件不變的情況下,氮、磷、鉀每減少1單位(1千克),可以使總成本降低的數量,所以對偶價格是不大於零的。也就是說,在其他條件不變的條件下如果每畝地對氮肥的需要量減少1千克,可使得施肥成本降低3.5元;如果每畝地對磷肥的需要量減少1千克,也可使得施肥成本降低3.5元;如果每畝地對鉀肥的需要量減少1千克,施肥成本不能降低,因為在最優施肥方案中鉀肥含量67.2千克遠遠超過了需要量42千克。這裡的對偶價格的相反數3.5、3.5、0分別是氮、磷、鉀邊際成本(Marginal costs)或者稱為影子成本(shadow costs)^[3]。如果線性規劃問題(LP3)是成本最小化的線性規劃問題,則其對偶線性規劃問題(DLP3)的最優解 $y 1 = 3.5, y - 2 = 3.5, y 3 = 0$ 就是各種質量指標的邊際成本。

[編輯]

影子成本的動態描述^[1]

　　根據影子成本的含義,在其他條件不變的情況下,隨著該種質量指標(效用)的提高其邊際成本具有增加的趨勢。以作物施肥的最小成本為例,在其他條件不變的情況下,隨著每畝氮肥需求量b1的增加,氮肥的邊際成本 $y 1$ 是 $b 1$ 的單調不減的階梯函數。在(LP3)中,利用LINDO6.1通過對氮肥的需求量 $b 1$ 進行敏度分析,可以得到氮肥的邊際成本 $y 1$ 隨著 $b 1$ 的變化而變化的函數表達式:

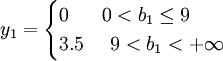
　　 $y_1=\begin{cases}0 \ \ \ \ \ 0<b_1 \le 9 \\ 3.5 \ \ \ \ 9<b_1< +\infty \end{cases}$

　　在(LP3)中,利用LINDO6.1通過對磷肥的需求量b2進行靈敏度分析,可以得到磷肥的邊際成本 $y 2$ 隨著 $b 2$ 的變化而變化的函數表達式:

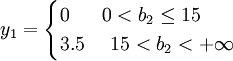
　　 $y_1=\begin{cases}0 \ \ \ \ \ 0<b_2 \le 15 \\ 3.5 \ \ \ \ 15<b_2< +\infty \end{cases}$

　　在(LP3)中,利用LINDO6.1通過對鉀肥的需求量 $b 3$ 進行靈敏度分析,可以得到鉀肥的邊際成本 $y 3$ 隨著 $b 3$ 的變化而變化的函數表達式:

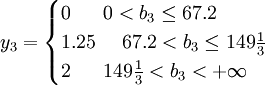
　　 $y_3=\begin{cases}0 \ \ \ \ \ 0<b_3 \le 67.2 \\ 1.25\ \ \ \ 67.2<b_3 \le 149\frac{1}{3} \\ 2 \ \ \ \ \ 149\frac{1}{3}<b_3<+\infty \end{cases}$

　　氮、磷、鉀邊際成本是氮、磷、鉀需求量的分段函數,這些分段函數都是單調不減的階梯形函數,並且是左連續的。說明隨著氮、磷、鉀的需求量增加,其邊際成本越來越大,因此我們應該在考慮邊際成本的條件下增加或者減少每畝土地氮、磷、鉀的需求,使得施肥效益與施肥成本達到最大的“性價比”。

　　對於使成本最小的產品生產的最優化問題,建立線性規劃問題的數學模型,使得在滿足各種質量指標要求的前提下成本最小。其各種指標的影子成本就是該種質量指標的邊際成本,隨著質量指標的提高,其邊際成本不斷增加;當然,適當降低某項質量指標可能使邊際成本減少。

[編輯]

影子價格與影子成本的惟一性討論^[1]

　　在對偶變數的經濟意義的研究中,大部分都是研究資源利用最大化問題的對偶線性規劃問題,解釋為資源的影子價格。有的將收益(或者利潤)最大化問題與成本最小化問題的對偶規劃問題的最優解混為一談,都稱為影子價格。筆者認為,應該根據所研究問題的不同而區別對待。

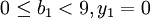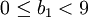　　當我們通過對線性規劃問題進行靈敏度分析研究影子價格或影子成本時,滿足最優基條件的區間是閉區間,錶面上看對應 $b i$ 的某一個取值, $y i$ 有兩個不同的值,影子價格不惟一。例如,在(LP3)中,通過求解可以得到:當 $0\le b_1<9,y_1=0$ ;當 $9\le b_1<+\infty,y_1=3.5$ 。錶面上看來,在其他條件不變的條件下,對應 $b 1 = 9$ ,有兩個影子成本 $y 1 = 0$ 和 $y 1 = 3.5$ ,但根據影子成本的經濟意義, $b 1 = 9$ 時討論減少 $b 1$ 引起總成本Z的降低, $b 1$ 的範圍是: $0\le b_1<9$ 。這種情況下只能認為 $b 1 = 9$ 在的影子成本是0而不是3.5。

　　文獻^[4]^[5]中都討論了影子價格不惟一的問題。即認為如果線性規劃問題(LP1)或(LP2)的最優基不惟一時,對偶線性規劃問題(DLP1)或(DLP2)的最優解也不惟一,那麼影子價格或影子成本也不惟一,這給管理決策帶來了困難^[4]^[5]。文獻^[6]認為影子價格應該具有惟一性,並且進行了重新定義^[7]。筆者認為,影子價格或影子成本是惟一的,之所以會認為不惟一是由於沒有真正理解影子價格或影子成本的經濟含義。

　　資源利用問題的影子價格應該理解為:在某一範圍內,某種資源增加一個單位,可以使得總收益(總利潤)增加的數量。因此,在討論在 $b i$ 某個區間的取值的影子價格時, $b i$ 的變化範圍應該包含這個區間的左端點而不應該包含這個區間的右端點。因為在右端點增加 $b i$ 的值將超出這個範圍。因此,在其他條件不變的情況下,影子價格 $y i$ 是資源限量b_i的單調不增的階梯形函數,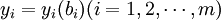 $y_i=y_i(b_i)(i=1,2,\cdots,m)$ 並且這個函數是右連續的。

　　質量指標(效用)問題的影子成本應該理解為:在某一範圍內,某種質量指標(效用)降低一個單位可以使得總成本減少的數量。因此,在討論 $b i$ 某個區間的取值的影子成本時,bi的變化範圍應該包含這個區間的右端點而不應該包含這個區間的左端點。因為在左端點減少 $b i$ 的值將超出這個範圍。因此,在其他條件不變的情況下,影子成本yi是質量指標bi的單調不減的階梯形函數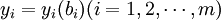 $y_i=y_i(b_i)(i=1,2,\cdots,m)$ ,並個函數是左連續的。

　　文獻^[4]中之所以誤認為甲乙丙三種資源的影子價格 $y 1, y 2, y 3$ 不惟一,是因 $b 1 = 12, b 2 = 8, b 3 = 16$ 的取值都是在影子價格發生變化的區間的端點。根據上述討論,影子價格是惟一的。文獻[3]中四種資源的影子價格的表達式分別為:

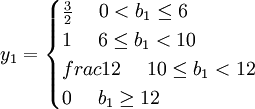
　　 $y_1=\begin{cases}\frac{3}{2} \ \ \ \ 0<b_1 \le 6 \\ 1 \ \ \ \ 6 \le b_1< 10 \\ frac{1}{2} \ \ \ \ 10 \le b_1<12 \\ 0 \ \ \ \ b_1\ge 12\end{cases}$

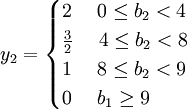
　　 $y_2=\begin{cases}2 \ \ \ \ 0\le b_2 < 4 \\ \frac{3}{2} \ \ \ \ 4 \le b_2< 8 \\1 \ \ \ \ 8\le b_2 <9 \\ 0 \ \ \ \ b_1\ge 9\end{cases}$

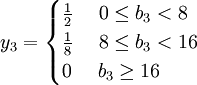
　　 $y_3=\begin{cases}\frac{1}{2} \ \ \ \ 0\le b_3 <8 \\ \frac{1}{8} \ \ \ \ 8 \le b_3< 16 \\0 \ \ \ \ b_3\ge 16 \end{cases}$

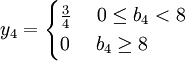
　　 $y_4=\begin{cases}\frac{3}{4} \ \ \ \ 0\le b_4 <8 \\ 0 \ \ \ \ b_4\ge 8 \end{cases}$

　　同樣,文獻^[5]中資源限量也都是影子價格發生變化的區間的端點,造成影子價格不惟一的誤解。文獻^[5]中兩種資源的影子價格的表達式分別為:

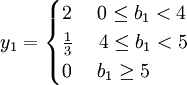
　　 $y_1=\begin{cases}2 \ \ \ \ 0\le b_1 < 4 \\ \frac{1}{3} \ \ \ \ 4 \le b_1< 5 \\ 0 \ \ \ \ b_1\ge 5 \end{cases}$

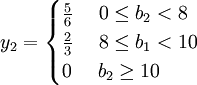
　　 $y_2=\begin{cases}\frac{5}{6} \ \ \ \ 0\le b_2 < 8 \\ \frac{2}{3} \ \ \ \ 8 \le b_1< 10 \\ 0 \ \ \ \ b_2\ge 10 \end{cases}$

[編輯]

影子成本在經濟管理中的應用^[1]

　　為了提高產品的某些質量指標,必需要增加成本,這時要將質量指標增加帶來的效益———邊際效益與邊際成本進行比較。如果邊際效益小於邊際成本,則這種單純地提高質量指標不能增加利潤,是不可取的;如果邊際效益大於邊際成本,則通過這種指標的提高可以增加利潤。因此,在經濟管理中,可以根據產品的某項質量指標的邊際效益與其邊際成本進行比較,當邊際效益大於邊際成本時,可以考慮適當提高該項質量指標直至邊際效益等於邊際成本;當邊際效益小於邊際成本時,可以考慮適當降低該項質量指標直至邊際效益等於邊際成本。因此,使成本最小的產品生產的最優化問題最終使得各種質量指標的邊際效益恰好等於邊際成本,這樣就能實現資源的最優配置。

　　當然,也可以將邊際成本作為同類企業的經濟效益評價指標。在同樣的條件下邊際成本小的企業,說明它的管理水平先進,適應市場的能力強,在資源配置中處於優先地位;邊際成本大的企業,說明它的管理水平比較落後,適應市場的能力弱,在資源配置中處於劣勢地位。

[編輯]

參考文獻

↑ ^1.0 ^1.1 ^1.2 ^1.3 楊桂元.影子價格與影子成本
↑ 楊桂元、唐小我.影子價格及其在資源配置中的應用[J].電子科技大學學報,2000,29(5):540-544.
↑ 張惠恩.管理線性規劃[M].大連:東北財經大學出版社,2001.18-31.
↑ ^4.0 ^4.1 ^4.2 林濤、劉家誠.關於影子價格不惟一的探討[J].廣西會計,1999,6:8-10.
↑ ^5.0 ^5.1 ^5.2 ^5.3 劉舒燕.關於資源影子價格不惟一問題的討論[J].運籌與管理,2001,10(2):33-36.
↑ 夏少剛、申樹斌、潘權.關於影子價格問題的討論[J].運籌與管理,2002,11(1):23-27.
↑ 夏少剛、申樹斌、潘權.關於影子價格問題的討論[J].運籌與管理,2002,11(1):23-27.

取自"https://wiki.mbalib.com/zh-tw/%E5%BD%B1%E5%AD%90%E6%88%90%E6%9C%AC"

打开MBA智库App, 阅读完整内容打开App

如果您認為本條目還有待完善，需要補充新內容或修改錯誤內容，請編輯條目或投訴舉報。

本条目由以下用户参与贡献

Cabbage.

頁面分類: 成本會計術語

評論(共1條)

提示:評論內容為網友針對條目"影子成本"展開的討論，與本站觀點立場無關。

马宏立 (討論 | 貢獻) 在 2011年10月17日 16:00 發表

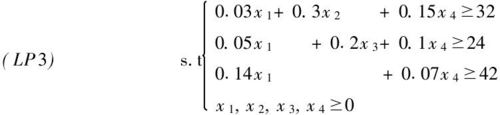
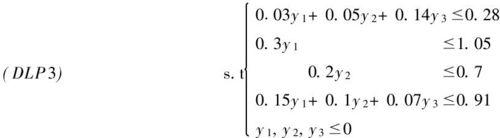
好\(^o^)/~！！！就是太高深了點------

回複評論

發表評論請文明上網，理性發言並遵守有關規定。

查看

工具▼

影子成本

出自 MBA智库百科(https://wiki.mbalib.com/)

目錄

影子成本概述^[1]

影子成本的動態描述^[1]

影子價格與影子成本的惟一性討論^[1]

影子成本在經濟管理中的應用^[1]

參考文獻

温馨提示

本条目相关课程

本条目由以下用户参与贡献

評論(共1條)

導航

意见反馈

查看

工具▼

影子成本

出自 MBA智库百科(https://wiki.mbalib.com/)

目錄

影子成本概述[1]

影子成本的動態描述[1]

影子價格與影子成本的惟一性討論[1]

影子成本在經濟管理中的應用[1]

參考文獻

温馨提示

本條目相關文檔

本条目相关课程

本条目由以下用户参与贡献

評論(共1條)

導航

意见反馈

影子成本概述^[1]

影子成本的動態描述^[1]

影子價格與影子成本的惟一性討論^[1]

影子成本在經濟管理中的應用^[1]