趨勢外推法
出自 MBA智库百科(https://wiki.mbalib.com/)
趨勢外推法(Trend extrapolation)
目錄 |
趨勢外推法(Trend extrapolation)是根據過去和現在的發展趨勢推斷未來的一類方法的總稱,用於科技、經濟和社會發展的預測,是情報研究法體系的重要部分。
趨勢外推的基本假設是未來系過去和現在連續發展的結果。
趨勢外推法的基本理論是:決定事物過去發展的因素,在很大程度上也決定該事物未來的發展,其變化,不會太大;事物發展過程一般都是漸進式的變化,而不是跳躍式的變化掌握事物的發展規律,依據這種規律推導,就可以預測出它的未來趨勢和狀態。
趨勢外推法首先由R.賴恩(Rhyne)用於科技預測。他認為,應用趨勢外推法進行預測,主要包括以下6個步驟:
(1)選擇預測參數;
(2)收集必要的數據;
(3)擬合曲線;
(4)趨勢外推;
(5)預測說明;
(6)研究預測結果在制訂規劃和決策中的應用。
趨勢外推法是在對研究對象過去和現在的發展作了全面分析之後,利用某種模型描述某一參數的變化規律,然後以此規律進行外推。
- 一、直線趨勢延伸法
預測目標的時間序列資料逐期增(減)量大體相等時,長期趨勢即基本呈現線性趨勢,便可選用直線趨勢延伸法進行預測。
遇到時間序列大多數數據點變化呈現線性,個別點有異常現象時,經過質數分析,可以在作數據處理(刪除或作調整)後再找線性趨勢直線進行預測。
直線趨勢延伸法與平滑技術(二次移動平均法和二次指數平滑法)同樣是遵循事物發展連續原則,以預測目標時間序列資料呈現有單位時間增(減)量大體相同的長期趨勢變動為適用條件的。
它們之間的區別為:
(1)預測模型的參數計算方法不同。直線趨勢延伸法模型參數靠最小二乘法數學推導;平滑技術主要靠經驗判斷決定或。
(2)線性預測模型中的時間變數的取值不同。直線趨勢延伸法中時間變數取值決定於未來時間在時間序列中的時序;平滑技術模型中的時間變數的取值決定於未來時間相距建模時點的時間周期數。
(3)模型適應市場的靈活性不同。直線趨勢延伸預測模型參數對時間序列資料一律同等看待,在擬合中消除了季節、不規則、迴圈三類變動因數的影響,反映時間序列資料長期趨勢的平均變動水平;平滑技術預測模型參數對時間序列資料則採用重近輕遠原則,在擬合中能較靈敏地反映市場變動的總體水平。
(4)隨時間推進,建模參數計算的簡便性不同。隨著時間推進,時間序列資料增加,直線趨勢延伸預測模型參數要重新計算,且與前面預測時點的參數計算無關;平滑技術模型參數同樣要重新計算,但與前面預測時點的參數計算是有關係的。
- 二、曲線趨勢法
市場商品的需求與供應,由於受到政策性因素、消費者心理因素、季節性因素等多種因素的影響,其變動趨勢並非都是一條直線狀態,有時會呈現出不同形狀的曲線變動趨勢。在這種情形下,就需要用曲線方程式求得曲線趨勢變動線,然後加以延伸,確定預測值。
由於影響市場的因素很多,使得曲線方程式多種多樣,主要有二次曲線法、三次曲線法、戈珀茲曲線法和指數曲線法。
- 三、簡單的函數模型
為了擬合數據點,實際中最常用的是一些比較簡單的函數模型,如線性模型、指數曲線、生長曲線、包絡曲線等。
線性趨勢外推法是最簡單的外推法。這種方法可用來研究隨時間按恆定增長率變化的事物。在以時間為橫坐標的坐標圖中,事物的變化接近一條直線。根據這條直線,可以推斷事物未來的變化。
應用線性外推法,首先是收集研究對象的動態數列,然後畫數據點分佈圖,如果散點構成的曲線非常近似於直線,則可按直線規律外推。
指數曲線法(Exponential curve)是一種重要的趨勢外推法。當描述某一客觀事物的指標或參數在散點圖上的數據點構成指數曲線或近似指數曲線時,表明該事物的發展是按指數規律或近似指數規律變化。如果在預測期限內,有理由說明該事物仍將按此規律發展,則可按指數曲線外推。
許多研究結果表明,技術發展,有時包括社會發展,其定量特性往往表現為按指數規律或近似指數規律增長,一種技術的發展通常要經過發生、發展和成熟3個階段。在技術發展進入階段之前,有一個高速發展時期。一般地說,在這個時期內,很多技術特性的發展是符合指數增長規律的。例如,運輸工具的速度、發動機效率、電站容量、電腦的存貯容量 和運算速度等,其發展規律均表現為指數增長趨勢。
對於處在發生和發展階段的技術,指數曲線法是一種重要的預測方法,一次指數曲線因與這個階段的發展趨勢相適應,所以比較適合處於發生和發展階段技術的預測,一次指數曲線也可用於經濟預測,因為它與許多經濟現象的發展過程相適應,二次指數曲線和修正指數曲線則主要用於經濟方面的預測。
生長曲線模型(Growth curve models)可以描述事物發生、發展和成熟的全過程,是情報研究中常用的一種方法。
生物群體的生長,例如人口的增加、細胞的繁瑣,開始幾乎都是按指數函數的規律增長的。在達到一定的生物密度以後,由於自身和環境的制約作用,逐漸趨於一穩定狀態。通過對技術發展過程的研究,發現也具有類似的規律。由於技術性能的提高與生物群體的生長存在著這種非嚴謹的類似,因而可用生長曲線模擬技術的發展過程。
生長曲線法幾乎可用來研究每個技術領域的發展,它不僅可以描述技術發展的基本傾向,而更重要的是,它可以說明一項技術的增長由高速發展變為緩慢發展的轉折時期,為規劃決策確定開發新技術的恰當時機提供依據。
有些經濟現象也符合或近似生長曲線的變化規律,因而它也完全可以用來研究經濟領域的問題。
1、概念
生長曲線描述一項單元技術的發展過程,而包絡曲線(Envelop curve)描述整個技術系統的發展過程。一項單元技術有功能特性上限,而由一系列先後相繼的單元技術構成的整個技術系統,不會因單元技術達到性能上限而停止發展。例如,把電腦作為整個技術系統,則分別以電子管→晶體管→中小規模集成電路到大規模集成電路作為邏輯元件的相應電腦就是它的單元技術。隨著單元技術的更替,電腦技術性能在不斷提高。
由於單元技術的連續更替,在時間—特性圖上表現為一系列的S曲線,隨時間的推移,後一條S曲線的性能比前一條S曲線的性能比前一條S曲線有所提高。如果把這一系列S曲線邊成一條包絡曲線,其形狀也往往是一條S曲線。R.艾爾斯(Ayres)通過對整個技術系統實際發展過程的觀察和分析,列舉了許多實例,用以說明整個技術系統的發展是符合包絡曲線規律的。例如:粒子加速器工作能量的增加,白熾燈效率的提高,航空發動機功率的增長,交通工具速度的提高等。
這些事實說明,整個技術系統的發展也是連續的,呈現某種規律性,符合或近似包絡曲線規律。這一規律是制訂長遠科技發展規劃的一個依據。
2、用途
用包絡曲線外推,可以估計某個技術系統的特性參數在未來某一時間將會達到什麼水平,適用於長期技術預測。此外,它還有以下兩個方面的實際用途:
①、用於分析新技術可能出現的時機
根據整個技術系統的特性參數遵循包絡曲線發展的規律,當某一單元技術的性能趨於其上限時,通常會有另一新的單元技術出現,推動整個技術系統的發展。按照這個原理,如果將包絡曲線法與生長曲線法結合起來使用,當現有技術的性能水平接近其上限時,規劃制訂者就應該估計,是否會有另一新的單元技術出現,從而相應地作出新技術的科研規劃和計劃,並加以實施,以保持產品的先進性。
②、用於驗證規劃中制訂的技術參數指標是否合理,為未來產品設計的功能特性參數提供評價依據。
如果目標規定的技術參數值訂在外推的包絡曲線之上,表明有可能冒進;反之,則可能是偏於保守的。
趨勢外推法的基本假設[1]
趨勢外推預測法和所有的時間序列分析一樣,都基於下邊兩個基本假設:
(1)決定事物過去發展的因素,在很大程度上仍決定事物的未來發展,這些因素作用的機理和數量關係是不變的,或變化不大。
(2)未來發展的過周屬於漸進過程,不是跳躍式的變化,即促使社會經濟現象不規則波動的因素,是不穩定的短期起作用的因素,它對社會經濟現象只產生局部的偶然影響。
趨勢外推法的主要目標[1]
趨勢外推法的主要目標,是根據過去經濟現象逐期增減變動的數量或比率,研究經濟發展變化的規律性,預測未來發展的趨勢。趨勢外推法也是一種模型預測法。模型法即數學模型法,就是用一個或一組數學方程(包括代數方程、微分方程或差分方程等)來表示所預測事物隨時間變化的形式或客觀事物之間的關係,來計算事物未來的變化與狀態,達到預測的目的。當數學模型代表事物隨時間變化的形式,就屬於趨勢外推預測技術。
趨勢外推法的研究問題[1]
趨勢外推法的數學模型很多,對數學模型的選用,既要分析有關預測對象的歷史數據,還要分析其未來發展的趨勢過程。主要研究的問題有:
1.預測參數是單調遞增還是單調遞減,是有一個或幾個極值,極值是穩定的還是周期變動的;
2.預測參數的極值是極大還是極小;
3.決定預測對象發展過程的函數有無拐點;
4.描述預測對象的函數是否具有對稱性;
5.預測對象的發展過程在時間上是否有明顯的限制等。
趨勢外推法的案例分析[1]
趨勢外推函數很多,常用的有線性函數、拋物線函數、指數函數、修正指數函數、雙曲線函數、羅古斯諦曲線函數、戈帕斯曲線函數及冪函數等。這裡採用指數曲線模型預測法。
- 1.預測模型的建立
在一個較長的時期里,分規格分工部的標準可比成本應該呈下降趨勢,並逐步逼近一個極限值。
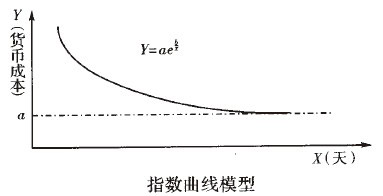
因為這種標準可比成本實際上是由物耗直接得出,各時期比較的是物耗,所以隨著生產技能的提高及生產設備的改進,生產定量的某種產品的物耗必然會降低,但是又不可能無限降低,所以長期來看應符合圖。中曲線走向。
上述曲線的方程Y = aeblX就是指數曲線模型.當a>0,b>0時,Y隨X增大單調遞減上凹,具有漸近線X=0和Y=a。當a>0,b<0時,Y單調遞增;在X的區間(0,-2/b)上,曲線上凹,且當X→0時,Y=0;X=-2/b,Y = aexp( − b2 / 2)為曲線拐點坐標;在X的開區間(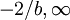 )上,曲線下凹,且以Y=a為漸近線。其中a、b為參數。X是時間,可以天為單位,也可以周、月為單位,但必須統一(這裡統一為天數)。為實際的綜合成本或可比成本,我們用歷史數據求出參數a、b確定模型,然後就可計算出趨勢值Y_i。方法如下:將
)上,曲線下凹,且以Y=a為漸近線。其中a、b為參數。X是時間,可以天為單位,也可以周、月為單位,但必須統一(這裡統一為天數)。為實際的綜合成本或可比成本,我們用歷史數據求出參數a、b確定模型,然後就可計算出趨勢值Y_i。方法如下:將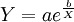 化歸為線性方程,兩邊取對數得:
化歸為線性方程,兩邊取對數得:
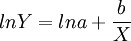 (1)
(1)
令u = lnY,A = lna,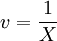 ,得:A+bv=u式(1)可看作是趨勢外推法中的直線模型。直線模型的關鍵是如何確定a、b參數,使其誤差最小。這裡選用最小二乘法。
,得:A+bv=u式(1)可看作是趨勢外推法中的直線模型。直線模型的關鍵是如何確定a、b參數,使其誤差最小。這裡選用最小二乘法。
最小二乘法是使實際值和趨勢值之差的平方和最小: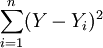 最小,即
最小,即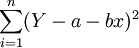 為最小。(假設這裡的Y就是u,即lnY;x是v,即1/X;要求的參數a、b就是對應的A、b)根據求最小值原理,對a、b求導數,並令其為零,即:
為最小。(假設這裡的Y就是u,即lnY;x是v,即1/X;要求的參數a、b就是對應的A、b)根據求最小值原理,對a、b求導數,並令其為零,即:
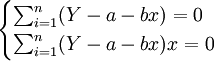 (2)
(2)
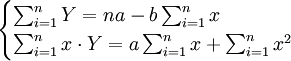 (3)
(3)
n為時間序列的項數,解此聯立方程,可求得a、b為:
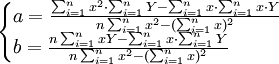 (4)
(4)
以上計算a、b時,代表天數的x值為0,1,2,…,起點為0,計算比較複雜。為了簡化計算,改變x值為…,-3,-2,-1,0,1,2,3,…;當天數為偶數時,用中間兩天的中點為零,即x值為…,-5,-3,-1,1,3,5,…。由此可得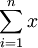 總是為零。於是式(4)可簡化為:
總是為零。於是式(4)可簡化為:
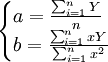 (5)
(5)
上述計算完成後,在用相應的參數A、b替換a、b,然後帶入解方程求出成本值。
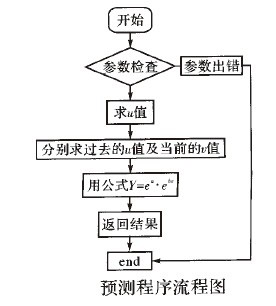
- 2.程式流程
程式流程如下圖所示。
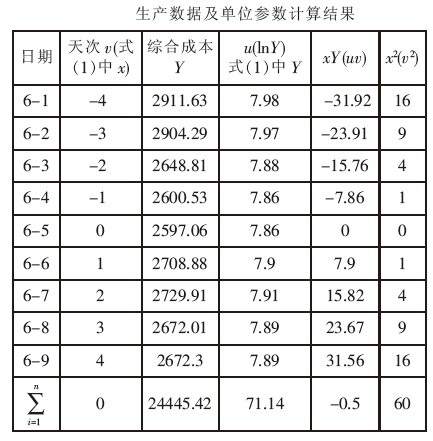
- 3.預測實例
取某鋼鐵鑄管集團公司在2001年六月份的日生產數據,如下表所示:
首先解出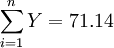 ,
,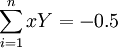 ,
,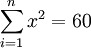 ,與n=9代入式(5)可得:
,與n=9代入式(5)可得:
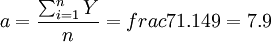 (即是式(1)中的A)
(即是式(1)中的A)
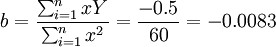
根據A的值及代換公式A = lna,可得a=2697.28,b不變,為方便起見v不代換。要預測6月10日的值,可帶入公式:Y = 2697.28e − 0.0083v;6月10日的自變數v的值應該是5,因此,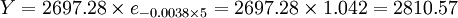 ,實際上6月10日的綜合成本是2718.15,誤差是3.4%,預測結果比較準確。
,實際上6月10日的綜合成本是2718.15,誤差是3.4%,預測結果比較準確。








很好.