移動平均法
出自 MBA智库百科(https://wiki.mbalib.com/)
移動平均法又稱滑動平均法、滑動平均模型法(Moving average,MA)
目錄 |
移動平均法是用一組最近的實際數據值來預測未來一期或幾期內公司產品的需求量、公司產能等的一種常用方法。移動平均法適用於即期預測。當產品需求既不快速增長也不快速下降,且不存在季節性因素時,移動平均法能有效地消除預測中的隨機波動,是非常有用的。移動平均法根據預測時使用的各元素的權重不同,可以分為:簡單移動平均和加權移動平均。
移動平均法是一種簡單平滑預測技術,它的基本思想是:根據時間序列資料、逐項推移,依次計算包含一定項數的序時平均值,以反映長期趨勢的方法。因此,當時間序列的數值由於受周期變動和隨機波動的影響,起伏較大,不易顯示出事件的發展趨勢時,使用移動平均法可以消除這些因素的影響,顯示出事件的發展方向與趨勢(即趨勢線),然後依趨勢線分析預測序列的長期趨勢。
移動平均法可以分為:簡單移動平均和加權移動平均。
一、簡單移動平均法
簡單移動平均的各元素的權重都相等。簡單的移動平均的計算公式如下: Ft=(At-1+At-2+At-3+…+At-n)/n式中,
- Ft--對下一期的預測值;
- n--移動平均的時期個數;
- At-1--前期實際值;
- At-2,At-3和At-n分別表示前兩期、前三期直至前n期的實際值。
二、加權移動平均法
加權移動平均給固定跨越期限內的每個變數值以不同的權重。其原理是:歷史各期產品需求的數據信息對預測未來期內的需求量的作用是不一樣的。除了以n為周期的周期性變化外,遠離目標期的變數值的影響力相對較低,故應給予較低的權重。 加權移動平均法的計算公式如下:
Ft=w1At-1+w2At-2+w3At-3+…+wnAt-n式中,
在運用加權平均法時,權重的選擇是一個應該註意的問題。經驗法和試演算法是選擇權重的最簡單的方法。一般而言,最近期的數據最能預示未來的情況,因而權重應大些。例如,根據前一個月的利潤和生產能力比起根據前幾個月能更好的估測下個月的利潤和生產能力。但是,如果數據是季節性的,則權重也應是季節性的。
使用移動平均法進行預測能平滑掉需求的突然波動對預測結果的影響。但移動平均法運用時也存在著如下問題:
1、 加大移動平均法的期數(即加大n值)會使平滑波動效果更好,但會使預測值對數據實際變動更不敏感;
2、 移動平均值並不能總是很好地反映出趨勢。由於是平均值,預測值總是停留在過去的水平上而無法預計會導致將來更高或更低的波動;
3、 移動平均法要由大量的過去數據的記錄。
案例一:移動平均法在公交運行時間預測中的應用[1]
公交車運行時間原始數據的採集採用的是人工測試法,即由記錄人員從起始點到終點跟蹤每輛客車,並記錄下車輛在每個站點之間的運行時間。行駛路線選用的是長春公交306路,始發站為長春大學,終點站為火車站。數據採集的日期是從2001年4月3日到4月5日。這三天屬工作日,因為公交運行時間因時間的不同而有不同的結果。所以這些數據只作為預測工作日運行時間。採集的數據是該路從工農廣場站點到桂林路站點之間的運行時間。
(1)N取3-20,利用移動平均法預測得到的結果見表1。
移動平均法預測表
| K | N | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | ||
| 6:40 | 15 | 5 | |||||||||||||||||
| 6:41 | 16 | 5 | 5 | ||||||||||||||||
| 6:41 | 17 | 4 | 4 | 4 | |||||||||||||||
| 6:42 | 18 | 4 | 4 | 4 | 4 | ||||||||||||||
| 6:43 | 19 | 4 | 4 | 4 | 4 | 4 | |||||||||||||
| 6:44 | 20 | 4 | 4 | 4 | 4 | 4 | 4 | ||||||||||||
| 6:45 | 21 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | |||||||||||
| 6:46 | 22 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | ||||||||||
| 6:47 | 22 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | |||||||||
| 6:48 | 23 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | ||||||||
| 6:49 | 24 | 5 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | |||||||
| 6:50 | 25 | 5 | 5 | 5 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | ||||||
| 6:51 | 26 | 5 | 5 | 5 | 5 | 5 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | ||||||
| 6:52 | 27 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 4 | 4 | 4 | 4 | 4 | 4 | |||||
| 6:53 | 28 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | ||||
| 6:54 | 29 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | |||
| 6:55 | 30 | 6 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | ||
| 6:56 | 31 | 6 | 6 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | |
| 6:57 | 32 | 6 | 6 | 6 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 |
| 6:58 | 33 | 6 | 6 | 6 | 6 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 |
| 6:59 | 34 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 |
| 7:00 | 35 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 |
| 7:01 | 36 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 |
| 7:02 | 37 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 |
| 7:03 | 38 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 |
| 7:04 | 39 | 4 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 |
| 7:05 | 40 | 4 | 4 | 4 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 |
| 7:06 | 41 | 4 | 4 | 4 | 4 | 4 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 |
| 7:07 | 42 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 |
| 7:08 | 43 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 |
| 7:09 | 44 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 5 | 5 | 5 | 5 | 5 | 5 | 5 |
| 7:10 | 45 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 5 | 5 | 5 | 5 | 5 |
| 7:11 | 46 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 5 | 5 | 5 |
| 7:12 | 47 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 5 |
| 7:13 | 48 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 |
| 7:14 | 49 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 |
| 7:15 | 50 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 |
| 7:16 | 51 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 |
| 7:17 | 52 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 |
| 7:18 | 53 | 5 | 5 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 |
| 7:19 | 54 | 5 | 5 | 5 | 5 | 5 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 |
| 7:20 | 55 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 |
| 7:21 | 56 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 |
| 7:22 | 57 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 4 | 4 | 4 | 4 | 4 | 4 | 4 |
| 7:23 | 58 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 4 | 4 | 4 | 4 | 4 | 4 |
| 7:24 | 59 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 4 | 4 | 4 | 4 |
| 7:25 | 60 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 4 | 4 | 4 | 4 |
| 7:26 | 61 | 4 | 4 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 4 | 4 | 4 | 4 |
| 7:27 | 62 | 4 | 4 | 4 | 4 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 4 | 4 | 4 | 4 |
| 7:28 | 63 | 4 | 4 | 4 | 4 | 4 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 4 | 4 | 4 |
| 7:29 | 64 | 4 | 4 | 4 | 4 | 4 | 4 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 4 | 4 |
| 7:30 | 65 | 5 | 4 | 4 | 4 | 4 | 4 | 4 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 4 |
| 7:31 | 66 | 5 | 4 | 4 | 4 | 4 | 4 | 4 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 |
| 7:32 | 67 | 5 | 5 | 5 | 4 | 4 | 4 | 4 | 4 | 4 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 |
| 7:33 | 68 | 5 | 5 | 5 | 5 | 4 | 4 | 4 | 4 | 4 | 4 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 |
| 7:34 | 69 | 5 | 5 | 5 | 5 | 5 | 4 | 4 | 4 | 4 | 4 | 4 | 5 | 5 | 5 | 5 | 5 | 5 | 5 |
| 7:35 | 70 | 5 | 5 | 5 | 5 | 5 | 5 | 4 | 4 | 4 | 4 | 4 | 4 | 5 | 5 | 5 | 5 | 5 | 5 |
| 7:36 | 71 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 4 | 4 | 4 | 4 | 4 | 4 | 5 | 5 | 5 | 5 | 5 |
| 7:37 | 72 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 4 | 4 | 4 | 4 | 4 | 4 | 5 | 5 | 5 | 5 |
| 7:38 | 73 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 4 | 4 | 4 | 4 | 4 | 4 | 5 | 5 | 5 |
| 7:39 | 74 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 4 | 4 | 4 | 4 | 4 | 4 | 5 | 5 |
| 7:40 | 75 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 4 | 4 | 4 | 4 | 4 | 4 | 5 |
| 7:41 | 76 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 4 | 4 | 4 | 4 | 5 |
| 7:42 | 77 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 |
| 7:43 | 78 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 |
| 7:44 | 79 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 |
| 7:45 | 80 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 |
| 7:46 | 81 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 |
| 7:47 | 82 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 |
| 7:48 | 83 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 |
| 7:49 | 84 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 |
| 7:50 | 85 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 |
| 7:51 | 86 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 |
| 7:52 | 87 | 4 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 |
| 7:53 | 88 | 4 | 4 | 4 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 |
| 7:54 | 89 | 4 | 4 | 4 | 4 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 |
| 7:55 | 90 | 4 | 4 | 4 | 4 | 4 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 |
| 7:56 | 91 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 |
| 7:57 | 92 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 |
| 7:58 | 93 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 5 | 5 | 5 | 5 | 5 | 5 | 5 |
| 7:59 | 94 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 5 | 5 | 5 | 5 | 5 | 5 |
| 8:00 | 95 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 5 | 5 | 5 | 5 |
| 8:01 | 96 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 5 | 5 | 5 |
| 8:02 | 97 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 5 |
| 8:03 | 98 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 |
| 8:04 | 99 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 |
| 8:05 | 100 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 |
| 8:06 | 101 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 |
| 8:07 | 102 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 |
| 8:08 | 103 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 |
| 8:09 | 104 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 |
| 8:10 | 105 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 |
| 8:11 | 106 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 |
| 8:12 | 107 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 |
| 8:13 | 108 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 |
| 8:14 | 109 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 |
| 8:15 | 110 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 |
| 8:16 | 111 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 |
| 8:17 | 112 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 |
| 8:18 | 113 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 |
| 8:19 | 114 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 |
| 8:20 | 115 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 |
| 8:21 | 116 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 |
| 8:22 | 117 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 |
| 8:23 | 118 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 |
| 8:24 | 119 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 |
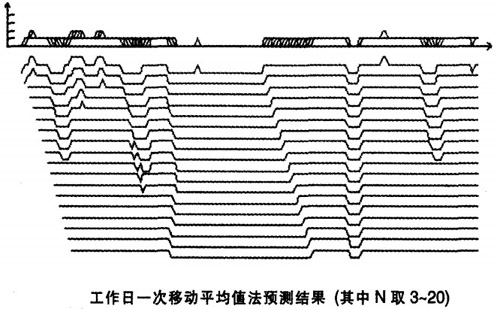
(2)N取3~20,得到的預測結果圖形見圖。
說明:橫坐標代表時間刻度,縱坐標代表所用時間(即預測時間);由於橫坐標時間刻度是一分鐘,所以無法體現每一刻度值,縱坐標刻度是2、4、6、8,單位是分鐘。其坐標的頂點坐標是(6:38,2)。
由預測結果圖形可以看出,當N的取值不同,所形成的曲線形狀大致相同,只是N的取值越大其形成的曲線就相對於前一N值所形成的曲線有一個滯後偏差,因為N每增加一次,做移動平均值預測時就忽略了其對應單位時間序列的數據值,因此有這一現象。
(3)N取3~20一次移動平均法工作日誤差指標如表2。
一次移動平均法工作日誤差指標
| N值 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 相對誤差 | 0.1424 | 01457 | 01389 | 0.1321 | 0.1502 | 0.1511 | 0.1478 | 0.1400 | 0.1455 |
| N值 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 相對誤差 | 0.1428 | 0.1409 | 0.1500 | 0.1510 | 0.1423 | 0.1470 | 0.1523 | 0.1655 | 0.1620 |
其中,相對誤差=1/N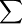 ||
|| ||/
||/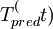 。
。
由上表可以看出,當預測日期為工作日時,相對誤差最小的是N=6時預測所得的數據。所以認為該參數最合適,並可作為工農廣場到桂林路站點之間公交車行程時間的預測依據。
案例二:簡單移動平均法在房地產中的運用[2]
某類房地產2001年各月的價格如下表中第二列所示。由於各月的價格受某些不確定因素的影響,時高時低,變動較大。如果不予分析,不易顯現其發展趨勢。如果把每幾個月的價格加起來計算其移動平均數,建立一個移動平均數時間序列,就可以從平滑的發展趨勢中明顯地看出其發展變動的方向和程度,進而可以預測未來的價格。
在計算移動平均數時,每次應採用幾個月來計算,需要根據時間序列的序數和變動周期來決定。如果序數多,變動周期長,則可以採用每6個月甚至每12個月來計算;反之,可以採用每2個月或每5個月來計算。對本例房地產2001年的價格,採用每5個月的實際值計算其移動平均數。計算方法是:把1~5月的價格加起來除以5得684元/平方米,把2~6月的價格加起來除以5得694元/平方米,把3~7月的價格加起來除以5得704元/平方米,依此類推,見表中第三列。再根據每5個月的移動平均數計算其逐月的上漲額,見表中第四列。
| 月份 | 房地產價格 實際值 | 每5個月的 移動平均數的 | 移動平均數 逐月上漲額 |
| 1 | 670 | ||
| 2 | 680 | ||
| 3 | 690 | 684 | |
| 4 | 680 | 694 | 10 |
| 5 | 700 | 704 | 10 |
| 6 | 720 | 714 | 10 |
| 7 | 730 | 726 | 12 |
| 8 | 740 | 738 | 12 |
| 9 | 740 | 750 | 12 |
| 10 | 760 | 762 | 12 |
| 11 | 780 | ||
| 12 | 790 |
假如需要預測該類房地產2002年1月的價格,則計算方法如下:由於最後一個移動平均數762與2002年1月相差3個月,所以預測該類房地產2002年1月的價格為:762 + 12 × 3 = 798(元/平方米)
案例三:加權移動平均法在計算銷售額中的運用[3]
某商場1月份至11月份的實際銷售額如表所示。假定跨越期為3個月,權數為l、2、3,試用加權移動平均法預測12月份的銷售額。
| 月份 | 銷售額 | 3個月的加權移動平均 |
| 1 | 38 | |
| 2 | 45 | |
| 3 | 35 | |
| 4 | 49 | 38.83 |
| 5 | 70 | 43.67 |
| 6 | 43 | 57.17 |
| 7 | 46 | 53.00 |
| 8 | 55 | 49.00 |
| 9 | 45 | 50.00 |
| 10 | 68 | 48.5 |
| 11 | 64 | 58.17 |
| 12 | 62.17 |
解: =38.83(萬元)
=38.83(萬元)
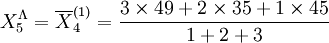 =43.67(萬元)
=43.67(萬元)
……
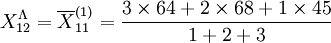 =62.17(萬元)
=62.17(萬元)
評論(共16條)
例子的原始數據在哪咧
文中有附上參考文獻,您可以查看一下
據機工版李華的《預測與決策教程》,一次移動平均法的預測值就是前N期的數學平均值,但據本頁案例2所述,則是“762 + 12 × 3 = 798(元/平方米)”,到底哪個的正確呢?————————特為此問題註冊。請教!
同時,在列表計算時,常把Mt寫在第t期的一行中,而不是寫在第(t-(N-1)/2)行中。經分析,案例2的預測結果是把一次移動平均法與二次移動平均法混在一起了,是錯誤的,望刪!上面我的問題因此也至此解決!
好像是沒有錯誤的,如果你覺得還有錯誤,你可以自己更改過來,並附上正確的參考來源分享給我們哦,MBA智庫是可以自己編輯分享的








例子看得不是很明白,不過其他的解釋挺好的