加權移動平均法
出自 MBA智库百科(https://wiki.mbalib.com/)
加權移動平均法(weighted moving average method/weighted moving average)
目錄 |
加權移動平均法就是根據同一個移動段內不同時間的數據對預測值的影響程度,分別給予不同的權數,然後再進行平均移動以預測未來值。
加權移動平均法不像簡單移動平均法那樣,在計算平均值時對移動期內的數據同等看待,而是根據愈是近期數據對預測值影響愈大這一特點,不同地對待移動期內的各個數據。對近期數據給予較大的權數,對較遠的數據給予較小的權數,這樣來彌補簡單移動平均法的不足。
加權平均法的計算公式如下:
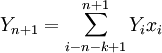
式中:
Yn + 1——第n+1期加權平均值;
Yi——第i期實際值;
x_i——第i期的權數(權數的和等於1);
n——本期數;
k——移動跨期;
用加權移動平均法求預測值,對近期的趨勢反映較敏感,但如果一組數據有明顯的季節性影響時,用加權移動平均法所得到的預測值可能會出現偏差。因此,有明顯的季節性變化因素存在時,最好不要加權。
案例一:加權移動平均法應用高校教師的考核業績[1]
當前,在高校薪酬分配中,一般對教師通過簡單統計年度業績考核結果來確定崗位津貼標準進行分配。筆者認為,這種辦法存在著很大的弊端,如年度科研業績的大起大落自然會造成教師收入水平的巨大波動,由此引起教師情緒上的波動以及其工作情境的變化,影響到工作效率,影響師資隊伍的穩定。用改進的加權移動平均法統計教師業績,並以此作為年度考核的依據將有效地消除年度考核業績的“大年”與“小年” 的現象,穩定教師的業績水平與收入水平,從而有助於吸引人才與穩定現有教師隊伍。本文嘗試著將加權移動平均法的“修勻”或“平滑”作用,應用於高校的年度業績考核,使不規則的序列數據,能夠平滑起來,利用經過修勻的年度考核數據作為有關津貼和獎金髮放的依據,能夠使教師的收入水平保持相對的穩定。
一、模型的討論
加權移動平均法常用於進行趨勢的預測,用這種辦法可以得到一個光滑的修正序列,即所謂的“修勻”。把修勻的功能應用於整理高校教師年度考核的序列數據應該同樣有效。
1.加權移動平均模型
加權移動平均模型是對移動平均模型的改進。採用加權移動平均,既可以做到按數據點的順序逐點推移,逐段平均,使不規則的數據點形成比較平滑的排列規則,又可以通過權數的設定使離考核期距離不同的數據,所起的作用不同。
加權移動平均法的統計模型為:
Mt = a1Yt − 1 + a2Yt − 2 + anYt − n (1)
式中:t——時間序列下標;
Mt ——第t期的移動平均數;
Yt ——第t期的觀察數據;
n——移動步長;
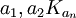 ——權數。
——權數。
2.數據的選取
(1)Yt的選取
選取某大學商學院中某位教師的業績考核數據作為樣本,因該學院對按業績決定教師報酬的做法執行得比較早且比較徹底,該教師從剛到學院工作至今有13個年頭,所以,所選取的數據樣本基本滿足作移動平均的要求,可以用來闡明用移動平均法來計算年度考核業績的合理性。
(2)n的選取
移動步長n的大小對移動平滑結果起決定性作用,選好n是加權移動平均法的關鍵。n值取得太小,模型靈敏度高,能較靈敏地反映近期的變化趨勢,但也可能對隨機干擾反映過度靈敏,據此得到的考核數據起伏劇烈,從而可能造成對被考核對象的誤判;n取得大時,對時間序列中包含的隨機變動的敏感性過低,以致不能敏銳地反映近期的變化趨勢,甚至會造成被考核對象在一段時間範圍內不努力但考核結果依然好的現象,如此也會造成對被考核對象的誤判。所以,在n的選取上,必須結合教師的教學尤其是科研工作的特點和業績考核的要求,以及各高校在考核方面的綜合實踐。這裡,將n設定為3。
(3)a1,a2,a3,的選取
為了使考核能夠更好地發揮激勵作用,在選取權數的時候,應使離考核期越近的權數越大。權數的選取,聽取了一些教育專家的建議,在綜合各方面的建議後,將分別a1,a2,a3分別設定為0.5、0.3和0.2。
這樣,用來計算考核業績的加權移動平均模型為:
Mt = 0.5Yt − 1 + 0.3Yt − 2 + 0.2Yt − 3 (2)
二、模擬計算及分析
1.利用加權移動平均計算的結果及分析
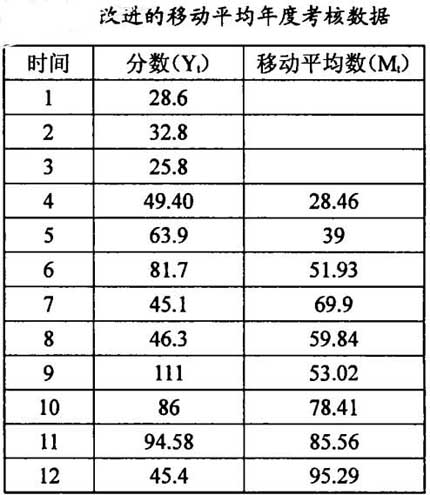
將各年度考核數據與根據公式(2)算得的加權移動平均數列入表1中。
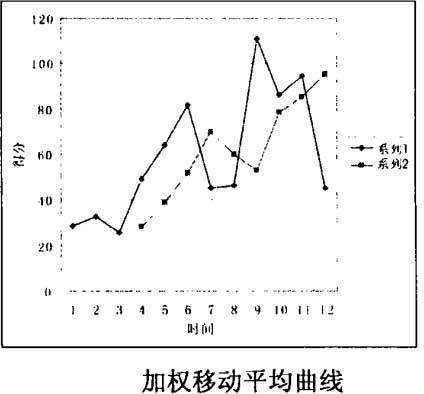
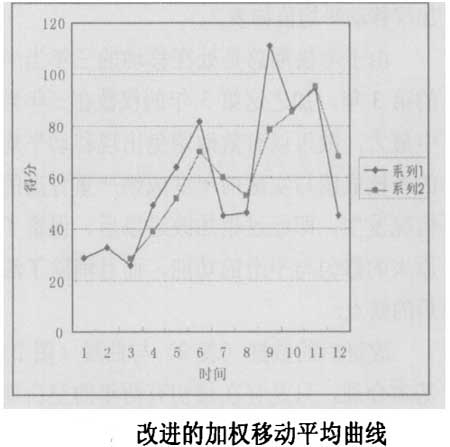
利用表1中數據繪得曲線,如圖:
上圖中的系列2曲線(加權移動平均曲線)明顯的比系列1曲線平緩,並且在所設定的情況下,更能體現上升的趨勢。所以利用系列2的加權移動平均數據代替系列1的簡單年度考核數據,能夠有效地避免出現與考核業績掛鉤的津貼和獎金大起大落的現象,即修勻的效果比較顯著。
但上述方法,也存在明顯不合理的情況:
(1)在移動步長取3的情況下,系列2的數據只能從第4年才開始,前三年都是空白(見上表的第3列)。而許多高校的考核一般都是從第1年就開始,第2年年初就開始與津貼掛鉤,即次年的津貼發放是根據前一年的考核成績。對於前三年出現空白考核業績的情況,在實際考核工作中,顯然不能接受。
(2)系列2出現明顯的滯後情況,如在第7年末和第12年末的年度實際考核業績很低,但加權移動平均得分卻非常高;而在第9年末的考核分數很高,但加權移動平均得分卻很低,明顯不合理。這種現象稱為加權移動平均的“滯後”現象。
2.改進的加權移動平均模型
改進加權移動平均模型的目的,是使在考核中應用該模型時,能夠繼續保持修勻與平滑的作用,又能夠避免滯後現象的發生。實際上在使用模型的目的僅僅是為了考核的特定情況下,只是對加權移動平均模型(2)稍加調整就可以滿足需要了。
在移動步長仍取3的情況下,將根據模型(2)算得的移動平均值向前移動一年,這樣,從第3年就有了移動平均得分,將滯後三年的情況改為滯後兩年。這樣改進後的加權移動平均公式就變為:
Mt = 0.5Yt − 0 + 0.3Yt − 1 + 0.2Yt − 2 (3)
根據改進的移動平均模型(3)算得的加權移動平均值如表2。
由於考核期總是處在移動的三年當中的第3年,加之這第3年的權數在三年當中最大,故可以有效地避免出現移動平均的考核成績與實際的年度成績嚴重背離的情況發生,即經過稍加改進以後,保留了原來的修勻與平滑的功能,而且消除了滯後的缺點。
改進後的數據(下表)與曲線(下圖)基本合理,只是存在最初有兩年的空白期問題。但是,在基本趨勢相同的情況下,可以取第1年與第2年末的實際得分作為來年津貼與獎金髮放的依據,然後,從第3年開始就可以接上改進的加權移動平均的考核分數了。如果考慮到新進青年博士教師科研啟動等的時間性問題,因而在最初的兩年當中只是作年度考核,但不與津貼與獎金掛鉤,到第三年以後再與津貼與獎金掛鉤的話,也許兩年空白期的矛盾就不存在了。
三、結論與建議
通過上述分析,得出如下結論:
1.簡單的年度考核業績往往是上下起伏不定的;
2.用加權移動平均的年度業績考核成績來代替簡單的年度考核成績能有效地避免起伏波動的現象,即能夠做到修勻與平滑;但造成與實際的年度業績嚴重背離的情況,即出現滯後現象;
3.用改進的加權移動平均年度考核成績取代簡單的年度考核成績,不僅可以有效避免大起大落的波動,而且還可以避免與實際的年度業績背離的情況發生。
所以,用改進的加權移動平均法來統計高校教師的年度考核成績,並以此作為有關津貼與獎金髮放的依據,能夠有效地排除由於某一年當中科研業績不佳造成實際年度考核成績差,從而津貼或獎金驟然減少,給教師帶來的不良心理影響。
- ↑ 山鳴峰,李雙,楊國巨集.用改進的加權移動平均法統計高校教師的考核業績[J].《中國高校師資研究》.2006,03









突然發現MBAlib好強大啊,比百度百科強太多了。