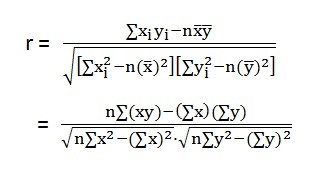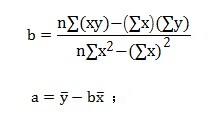直線趨勢法

出自 MBA智库百科(https://wiki.mbalib.com/)

直線趨勢法 (Linear Trend)

　　直線趨勢法又稱直線趨勢預測法、線性趨勢預測法，是對觀察期的時間序列資料表現為接近於一條直線，表現為近似直線的上升和下降時採用的一種預測方法。關鍵是求得趨勢直線，以利用趨勢直線的延伸求得預測值。

　　直線趨勢法是假設所要預測的變數與時間之間成線性函數關係，並以此為基礎預測未來。因此，用這種方法時，應先計算相關係數，以判別變數與時間之間是否基本上存線上性聯繫。只有存線上性聯繫時，才能採用這種方法進行預測。

　　求趨勢直線的方程式是：

　　Yt=a+bx

　　式中：x--自變數，是選定的任何x值；

　　Yt--因變數，對於選定的x值，相應變數Y的平均估計值，即第t預測周期的預測值；

　　a、b--未知參數

　　計算步驟：

　　1．根據一致的數據，計算相關係數r。

　　相關係數r是一個在0和正負1之間的繫數。相關係數等於0，表示變數間不存在直線相關關係； 如為±0.2或±0.3左右，表示低度相關；若為±0.6左右，為中度相關；若為±0.8以上，為高度相關；相關係數等於±1，為完全相關。相關係數是正數，為正相關；相關係數是負數，為負相關。

　　若r接近1，則可用一條直線y＝a＋bx 來描述預測變數隨時間的變動趨勢；

　　2．根據歷史數據，利用一元回歸法求出a、b值

　　3．利用求得的直線方程，其可預測未來期間（x）的預測變數（y）的值。

　　直線趨勢法的步驟為：

　　1.利用已知數據繪圖，確定直線趨勢。

　　2.求變動趨勢直線。可以用直觀法，也可以用最小二乘法。

　　3.利用變動趨勢直線的延伸，確定預測值。