二次曲線法

用手机看条目

出自 MBA智库百科(https://wiki.mbalib.com/)

什麼是二次曲線法

　　二次曲線法是研究時間序列觀察值數據隨時間變動呈現一種由高到低再到高(或由低到高再到低)的趨勢變化的曲線外推預測方法.由於時間序列觀察值的散點圖呈現拋物線形狀,故也稱之為二次拋物線預測模型。

　　假設曲線趨勢外推預測模型為：

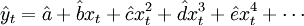
　　 $\hat y_t=\hat a+\hat b x_t+\hat c x_t^2+\hat dx_t^3+\hat e x_t^4+\cdots$

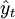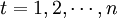　　式中： $\hat y_t$ 第t期某變數的預測值（因變數）； $x t$ ——時間變數（自變數）， $t=1,2,\cdots,n$ 。

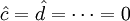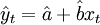　　1) 當 $\hat c=\hat d=\cdots=0$ 時， $\hat y_t=\hat a +\hat b x_t$ ，即為線性趨勢外推預測法的模型；

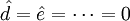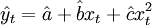　　2) 當 $\hat d=\hat e=\cdots=0$ 時， $\hat y_t=\hat a +\hat b x_t+\hat c x_t^2$ ,即為二次曲線外推預測法的模型。

[編輯]

二次曲線法的計算^[1]

　　用最小二乘法確定待定參數

　　1) 參數的確定

　　設 $y t$ 表示第t期的時間序列的觀察值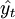； $\hat{y_t}$ ——第t期的預測值； $e t$ ——第t期的離差；Q——離差平方和。由二次曲線外推預測法的模型 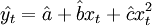$\hat{y_t}=\hat a+\hat bx_t +\hat cx_t ^2$ ，有

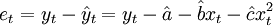
　　 $e_t=y_t-\hat y_t=y_t-\hat a-\hat bx_t-\hat cx_t^2$

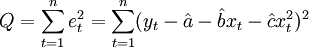　　 $Q=\sum_{t=1}^{n}e_t^2=\sum_{t=1}^{n}(y_t-\hat a-\hat bx_t-\hat cx_t^2)^2$ (3.2.2)

　　與擬合直線外推法相同的原理，對式（3.2.2）求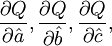 $\frac{\partial Q}{\partial\hat a},\frac{\partial Q}{\partial\hat b},\frac{\partial Q}{\partial\hat c},$ 並分別令其等於0，則可得關於 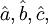$\hat a,\hat b,\hat c,$ 的方程組

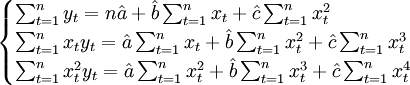　　 $\begin{cases}\sum_{t=1}^n y_t=n\hat a+\hat b\sum_{t=1}^n x_t+\hat c \sum_{t=1}^n x_t^2 \\ \sum_{t=1}^n x_t y_t=\hat a\sum_{t=1}^n x_t+\hat b\sum_{t=1}^n x_t^2+\hat c \sum_{t=1}^n x_t^3 \\ \sum_{t=1}^n x_t^2 y_t=\hat a\sum_{t=1}^n x_t^2+\hat b\sum_{t=1}^n x_t^3+\hat c \sum_{t=1}^n x_t^4 \end{cases}$ (3.2.3)

　　由於 $x t$ 表示時間序列的編號，如同擬合直線方程法一樣，當時間序列觀察期的項數為奇數時，令其中間項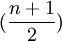 $(\frac{n+1}{2})$ 的編號為0，則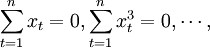 $\sum_{t=1}^n x_t=0,\sum_{t=1}^n x_t^3=0,\cdots,$

　　式(3.2.3)可簡化為：

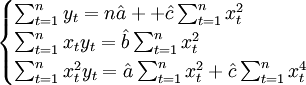　　 $\begin{cases} \sum_{t=1}^n y_t=n\hat a++\hat c \sum_{t=1}^n x_t^2 \\ \sum_{t=1}^n x_t y_t=\hat b\sum_{t=1}^n x_t^2 \\ \sum_{t=1}^n x_t^2 y_t=\hat a\sum_{t=1}^n x_t^2+\hat c \sum_{t=1}^n x_t^4 \end{cases}$ (3.2.4)

　　解上面的方程組可得：

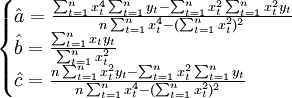　　 $\begin{cases} \hat a=\frac{\sum_{t=1}^n x_t^4 \sum_{t=1}^n y_t-\sum_{t=1}^n x_t^2\sum_{t=1}^n x_t^2y_t}{n\sum_{t=1}^n x_t^4-(\sum_{t=1}^n x_t^2)^2} \\ \hat b=\frac{\sum_{t=1}^n x_t y_t}{\sum_{t=1}^n x_t^2} \\ \hat c=\frac{n\sum_{t=1}^n x_t^2 y_t-\sum_{t=1}^n x_t^2 \sum_{t=1}^n y_t}{n\sum_{t=1}^n x_t^4-(\sum_{t=1}^n x_t^2)^2} \end{cases}$ (3.2.5)

　　2) 預測步驟

　　例3.4某公司1995～2003年的商品銷售收入如表3.4所示，試預測該公司2004年的銷售收入。

表3.4某公司1995～2003年商品銷售收入數據表 (單位：萬元)
年份	1995	1996	1997	1998	1999	2000	2001	2002	2003
銷售收入	545	641	764	923	1107	1322	1568	1836	2140

　　解：

　　①繪製散點圖如圖3.3所示。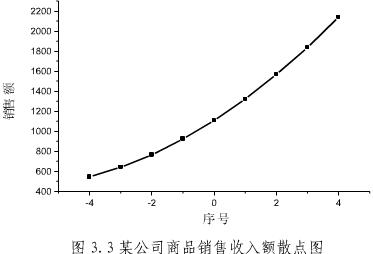

　　②根據觀察值的散點圖的變化趨勢確定其屬於二次曲線變化趨勢後，列表計算二次曲線待定參數所需的數據。計算結果如表3.5所示。

　　③計算待定參數，建立預測模型，並計算預測值。

　　利用表3.5中的有關數據，代入式（3.2.5）中，計算得：

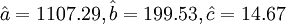
　　 $\hat a=1107.29,\hat b=199.53,\hat c=14.67$

　　該例的二次曲線的趨勢外推預測模型為：

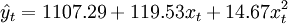　　 $\hat y_t=1107.29+119.53 x_t+14.67 x_t^2$ （3.2.6）

　　當x_t=5時，代入上式得

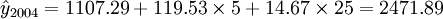　　 $\hat y_{2004}=1107.29+119.53\times 5+14.67\times 25=2471.89$ （萬元）

表3.5某公司商品銷售收入及有關數據計算表（單位：萬元）
年份	$x t$	銷售額 $y t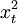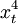$	$x_t^2$	$x_t^4$	$x t y t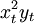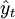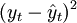$	$x_t^2 y_t$	$\hat y_t$	$(y_t-\hat y_t)^2$
1995	-4	545	16	256	2180	8720	543.89	1.23
1996	-3	641	9	81	-1923	5769	640.73	0.07
1997	-2	764	4	16	-1528	3056	766.91	8.47
1998	-1	923	1	1	-923	923	922.43	0.32
1999	0	1107	0	0	0	0	1107.29	0.08
2000	1	1322	1	1	1322	1322	1321.49	0.26
2001	2	1568	4	16	3136	6272	1565.03	8.82
2002	3	1836	9	81	5508	16524	1837.91	3.65
2003	4	2140	16	256	8560	34240	2140.13	0.02
$\sum$	0	10846	60	708	11972	76826		22.92