擬合直線方程法
出自 MBA智库百科(https://wiki.mbalib.com/)
目錄 |
擬合直線方程法，是指對銷售預測目標具有直線性變動趨勢的歷史時間數列，擬合成直線方程進行銷售預測外推法。
假設時間數列觀察期的編號為自然編號，當X分別為1，2，3，4…時，Y及其一級增長量如下表所示。
由上表從理論上說直線方程Y＝a+bX的一階差分別為一個常數，即每當X增加l時，Y值相應增加或減少一個b值。在實際操作中，如果原始數據的移動平均值的一階差分趨近於某一常數，則可將原始數據擬合成直線趨勢外推模型。
擬合直線方程，首先要求出參數a,b。求a,b的方法有多種，這裡只介紹最小二乘法、半平均法。
擬合直線方程法是最簡單的一種趨勢外推預測法,它是根據時間序列數據的長期變動趨勢,運用數理統計方法,確定待定參數,建立直線預測模型,並用之進行預測的一種定量預測分析方法。
設擬合直線方程為
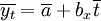
式中,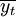
為第t期的預測值; x1為自變數,表示第t期的編號的
取值;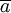 
為趨勢直線在y軸上的截距; 
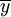為趨勢直線的斜率。
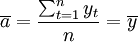
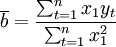
擬合直線方程法進行旅游需求的預測步驟[1]
在《中國旅游統計年鑒》中提取1992年至1998年中,1月份和3月份外國人入境旅游人數作為觀測值,進行1999年和2000年1月份和3月份的旅游需求預測,並與實際入境旅游人數做比較,最後算出預測值與實際值的誤差百分比。
(1)列表1計算求待定繫數所需的數據資料
表:1992年至1998年中,1月份外國人入境旅游人數及擬合直線方程法計算表
| 年份 | 觀測值y1 | xt | 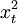 | xtyt |
| 1992 | 216552 | -3 | 9 | -649656 |
| 1993 | 263099 | -2 | 4 | -526198 |
| 1994 | 318748 | -1 | 1 | -318748 |
| 1995 | 344154 | 0 | 0 | 0 |
| 1996 | 446305 | 1 | 1 | 446305 |
| 1997 | 499714 | 2 | 4 | 999428 |
| 1998 | 460761 | 3 | 9 | 1382283 |
| 總計 | 2549333 | 0 | 28 | 1333414 |
(2)確定待定繫數,建立預測模型
根據上表數據可得:
。
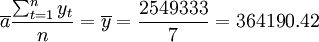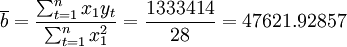
直線方程為
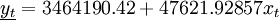
(3)用擬合直線方程求預測值
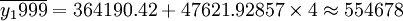
同理,可預測1999年2—12月份外國人入境旅游人數,與實際人數做對比,可得下表。
1999年1月——12月份外國人入境旅游人數
| 1999年 | 實際人數 | 預測人數 |
| 1月 | 529323 | 554678 |
| 2月 | 494216 | 541764 |
| 3月 | 690393 | 686900 |
| 4月 | 716292 | 731620 |
| 5月 | 724188 | 697112 |
| 6月 | 693599 | 655526 |
| 7月 | 718341 | 680410 |
| 8月 | 769209 | 762372 |
| 9月 | 769967 | 697649 |
| 10月 | 887492 | 816708 |
| 11月 | 776649 | 727728 |
| 12月 | 662627 | 655747 |
| 總計 | 8432296 | 8208214 |
直線趨勢外推預測法只適用於時間序列數據呈直線趨勢上升(或下降)變化,對時間序列數據,不論其遠近如何都一律同等看待。用最小二乘原理擬合的直線方程消除了不規則因素的影響,使趨勢值都落在擬合直線上,從而消除了不規則變動。
通過預測值與實際值的比較,能夠體現出用擬合直線方程法進行旅游需求預測,在實際應用過程中具有一定的準確性和實際應用價值。
- ↑ 夏冰,富強,徐海靜等.數學方法在經濟領域中的應用——利用擬合直線方程法進行旅游需求預測[J].金融理論與教學,2008,(4)
