加權擬合直線方程法

用手机看条目

出自 MBA智库百科(https://wiki.mbalib.com/)

加權擬合直線方程法的原理

　　加權擬合直線方程法是要數據資料要按照時間先後本著重近輕遠的原則，對離差平方和進行賦權，然後再按最小二乘原理，使離差平方和達到最小，求出加權擬合直線方程的過程。

　　擬合直線方程法根據最小二乘原理，使觀察值對於估計值的離差平方和 $Q=\sum(y_t-\overline{y})^2$ 達到最小，再應用數學上求偏導數並令之等於零的求極值方法計算待定參數a、b，然後建立直線方程並用來預測。但此法存在缺陷是在擬合直線過程，對時間序列數據不分遠期或近期，都一視同仁，同等對待。然而，實際上往往近期的數據資料對預測值的影響比遠期的數據資料要重要得多。因此，在市場預測的實踐中，要按照時間先後本著重近輕遠的原則，對離差平方和進行賦權，然後再按最小二乘原理，使離差平方和達到最小，求出加權擬合直線方程的過程，稱為加權擬合直線方程法。

　　假設：由近及遠的離差平方和的權重分別為： $a^0,a^1,a^2\ldots,a^{n-1}$ 其中0≤a＜l。當 $a 0 = 1$ 時，說明對最近期數據賦予最大權重為l，而後由近及遠，按a比例遞減。各期權數衰減速度取決於a的取值，a取值越大(越接近於1)，則衰減速度越慢；反之，a的取值越小(越接近於0)，則衰減速度越快。如a=1,則轉化為如上述的非加權擬合直線方程法。

[編輯]

加權擬合直線方程法的數學模型^[1]

　　假設加權擬合直線方程為

　　 $\overline{y}_t=\overline{a}+\overline{b}x_1$

　　加權離差平方和為

　　 $Q=\sum_{t=1}^n a^{n-1}(y_t-\overline{a}-\overline{b}x_1)$ (1)

　　要使Q達到最小,應用多元函數求極值的方法,對(1)式分別求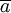 $\overline{a}$ 與 $\overline{b}$ 的偏導數。

　　 $\frac{\partial Q}{\partial\overline{a}}=-2[\sum_{t=1}^n a^{n-1}y_t-\overline{a}\sum_{t=1}^n a^{n-1}-\overline{b}\sum_{t=1}^n a^{n-1}x_1]$

　　 $\frac{\partial Q}{\partial\overline{b}}=-2[\sum_{t=1}^n a^{n-1}x_t y_t-\overline{a}\sum_{t=1}^n a^{n-1}x_t-\overline{b}\sum_{t=1}^n a^{n-1}x_t^2]$

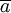　　並令 $\overline{a}$ 與 $\overline{b}$ 的偏導數均為0,即

　　 $\sum_{t=1}^n a^{n-1}y_t-\overline{a}\sum_{t=1}^n a^{n-1}-\overline{b}\sum_{t=1}^n a^{n-1}x_t$ 　　(2)

　　 $\sum_{t=1}^n a^{n-1}x_t y_t-\overline{a}\sum_{t=1}^n a^{n-1}x_t-\overline{b}\sum_{t=1}^n a^{n-1}x_t^2$ 　　(3)

　　對(2)(3)兩式聯立方程,進行求解,即可得到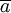 $\overline{a}$ 和 $\overline{b}$ 的值。

[編輯]

加權擬合直線方程法案例分析

[編輯]

案例一:加權擬合直線方程法在旅游需求預測中的應用^[1]

　　一、問題的提出

　　在旅游業比較發達的國家,計量經濟學已應用到旅游經濟研究之中.1961年,隨著一篇名為《國際市場上旅游商品與服務的需求》的文章問世,旅游需求預測引起了人們的關註.1973年, Strazhein、Harrop等人應用旅游需求收入彈性和價格彈性解釋了國際旅游需求的高速發展.1991年, Sung Soo Pyp在《旅游需求的線性消費模型》中成功地運用模型分析了價格、收入、時間等因素對旅游需求的影響.目前,國內對旅游需求預測並未引起學術界和旅游界人士的太多關註,相關文獻不多。下麵應用趨勢外推預測法中的加權擬合直線方程法,對海外人士來哈爾濱旅游需求進行預測,並通過實際的旅游人數進行驗證、探討此方法的準確性、可行性。

　　二、加權擬合直線方程法

　　任何預測方法都是某種推測或推斷,而對時間序列而言,推測與推斷都是一種外推。趨勢外推預測法是根據事物發展的特有規律,推測並著重研究其發展的可能趨勢,並通過建立適當的預測模型,推斷其未來變化的趨勢。

　　趨勢外推預測法的兩個前提假設是:

　　假設一:技術或經濟的發展因素,不但決定了過去的技術或經濟的發展,而且在很大程度上也決定著該技術的未來發展.這一前提假設實質上,指的是在研究某項技術的過去、現在和未來的整個發展過程中,內外、因素保持相對不變.假設二:技術或經濟的發展過程,一般屬於漸進變化,而不是跳躍性變化。

　　趨勢外推預測法分為擬合直線方程法和加權擬合直線方程法。在此我們採用加權擬合直線方程法進行旅游需求預測。

　　1)加權擬合直線方程法的原理

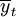　　預測的基本思想是使預測結果與實際數據的誤差的平方和達到最小.誤差平方和 $\sum_{t=1}^n(y_t-\overline{y}_t)^2$ 是每年旅游人數的實際值 $y t$ 與該年旅游人數的預測值 $\overline{y}_t$ 的偏差值的平方和,這就意味著∑ $\sum_{t=1}^n(y_t-\overline{y}_t)^2$ 中的每一項都有同樣的重要性,即無論這個誤差是近期的還是遠期的,都賦予同等的權數.但實際上,對於預測精度來說,近期的誤差比遠期的誤差更為重要.因此,在經濟預測的實踐中,要按時間先後,本著重近輕遠的原則,對離差平方和進行賦權,然後再按最小二乘原理,使離差分平方和達到最小,求出加權擬合直線方程.這種方法稱為加權擬合直線方程法。

　　二、對海外人士來哈爾濱旅游需求預測分析

　　以1996年至2001年海外人士來哈爾濱旅游人數作為觀測值,對2002、2003年至2006年進行旅游需求預測,並與實際旅游人數做比較,分析、探討.取a=0.5,分別計算各年的 $n-t,a^{n-1},y_t,a^{n-t}x_t y_t,a^{n-t}x_t,a^{n-t}x^2_t,$ 併列表如下表所示。

　　1996年至2001年海外來哈爾濱市旅游人數及加權擬合直線方程法計算表

年份	1996	1997	1998	1999	2000	2001	求和
$x t$	1	2	3	4	5	6
觀測值 $y t$	5	4	3	2	1	0
$n - t$	0.03125	0.0625	0.125	0.25	0.5	1	1.96875
$a n - 1, y t$	3139.344	7524.188	16556.38	36151.5	77541.5	169722	310634.9
$a n - t x t y t$	3139.344	15048.38	49669.13	144606	387707.5	1018332	1618502
$a n - t x t$	0.03125	0.125	0.375	1	2.5	6	10.03125
$a^{n-t}x^2_t$	0.03125	0.25	0.125	4	12.5	36	53.90625

　　確定待定繫數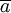 $\overline{a}$ 和 $\overline{b}$ ,建立預測模型 $\overline{y}_t=\overline{a}+\overline{b}x_1$ 。

　　由(2)(3)及表1可知

　　 $\begin{cases}310634.9-1.96875\overline{a}-10.03125\overline{b}=0\\1618502-10.03125\overline{a}-53.90625\overline{b}=0\end{cases}$

　　聯立解方程組,求解得 $\overline{a}\approx92614.62,\overline{b}\approx12790$ 。故預測模型為

　　 $\overline{y}=92614.62+12790x_t$

　　用此模型求2002、2003至2006年的預測值

　　當 $x t = 7$ 時, $\overline{y}_2002=92614.62+12790\times7=182144.6$ 即預測2002年海外來哈旅游人數約為182144.6人.下麵列出由此預測模型計算出的預測值與實際旅游人數相對照。

　　1996年至2006年海外來哈爾濱市旅游人數預測值與實際旅游人數對照表

年份	1996	1997	1998	1999	2000	2001	2002	2003	2004	2005	2006
預測值	105405	118195	130985	143775	156565	169355	182145	194935	207725	220515	233305
實際值	100459	120387	132451	144606	155083	169722	184253	145538	183818	203901	237498

　　由上表我們看到1996~2001擬合的效果非常好。2002的預測準確率比較高,而2003準確率極低,2004、2005準確率也不高。但是2006預測準確率又比較高.我們反思2003年就不足為奇了。2003年是非典時期,它嚴重影響、干擾了旅游業的發展,因而出現了較大的跳動。為了探討加權擬合直線方程法在旅游需求預測中的有效性。不妨以這一時期開始的實際數據作為觀測值,進行下一個預測。即以2003年~2006年海外人士來哈爾濱旅游人數作為觀測值,對2007年至2008年進行旅游需求預測。

　　仍取a=0.5,分別計算各年的 $n-t,a^{n-1},y_t,a^{n-t}x_t y_t,a^{n-t}x_t,a^{n-t}x^2_t,$ 併列表如下表所示。

　　2003年至2006年海外來哈爾濱市旅游人數及加權擬合直線方程法計算表

年份	2003	2004	2005	2006	求和
$x t$	1	2	3	4
觀測值 $y t$	145538	183818	203901	237498
$n - t$	3	2	1	0
$a n - 1$	0.125	0.25	0.5	1	1.875
$a n - 1, y t$	18192.25	45954.5	101950.5	237498	403595.3
$a n - t x t \| \| y t$	18192.25	91909	305851.5	949992	1365945
$a n - t x t$	0.125	0.5	1.5	4	6.125
$a^{n-t}x^2_t$	0.125	1	4.5	16	21.625

　　確定待定繫數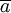 $\overline{a}$ 和 $\overline{b}$ ,建立預測模型。由(2)(3)及上表可知

　　 $\begin{cases}403595.3-1.875\overline{a}-6.125\overline{b}=0\\1365945-6.125\overline{a}-21.625\overline{b}=0\end{cases}$

　　聯立求解得 $\overline{a}\approx119203.4,\overline{b}\approx29402.28$ 。故預測模型為

　　 $\overline{y}=119203.4+29402.28x_t$

　　預測2007、2008年的旅游人數為

　　當 $x t = 5$ 時, $\overline{y}_2007=119203.4+29402.28\times5=266214.8$

　　當 $x t = 6$ 時 $\overline{y}_2008=119203.4+29402.28\times6=295617.08$

　　列出由此預測模型計算出的預測值與實際旅游人數相對照。

　　2003年至2008年海外來哈爾濱市旅游人數預測值與實際旅游人數對照表

年份	2003	2004	2005	2006	2007	2008
預測值	148605.7	178008	207410.2	236812.5	266214.8	295617.1
實際值	145538	183818	203901	237498	269628

　　由此我們看到以2003年~2006年旅游人數作為觀測值,預測2007年旅游人數準確率是比較高的.誤差不超過2%.2008年的旅游人數預測已經得出。這還要2008年末實際旅游人數來考證.我們將拭目以待。通過旅游人數的預測,我們也看到,拋開非典特殊時期,總體來說,哈爾濱旅游業的發展是比較平穩的。逐年呈線性上升趨勢。

　　通過上述海外來哈爾濱旅游人數預測值與實際旅游人數對比,能夠體現出加權擬合直線法在實際應用過程中具有較好的的準確率。其數學模型簡單,計算方法簡便、易行.易於旅游界人士操作.但是值得強調的是,應用加權擬合直線法進行旅游需求預測前提,必須是旅游業的平穩發展.如果有一些干擾因素.那末在預測時,必須綜合分析。

[編輯]

參考文獻

↑ ^1.0 ^1.1 孫偉.加權擬合直線方程法在旅游需求預測中的應用[J].數學的實踐與認識,2009,39(2)

取自"https://wiki.mbalib.com/zh-tw/%E5%8A%A0%E6%9D%83%E6%8B%9F%E5%90%88%E7%9B%B4%E7%BA%BF%E6%96%B9%E7%A8%8B%E6%B3%95"

打开MBA智库App, 阅读完整内容打开App

如果您認為本條目還有待完善，需要補充新內容或修改錯誤內容，請編輯條目或投訴舉報。

本条目由以下用户参与贡献

Yixi,Tiffany,HEHE林,KAER.

頁面分類: 統計方法

評論(共0條)

提示:評論內容為網友針對條目"加權擬合直線方程法"展開的討論，與本站觀點立場無關。

發表評論請文明上網，理性發言並遵守有關規定。

查看

工具▼

加權擬合直線方程法

出自 MBA智库百科(https://wiki.mbalib.com/)

目錄

加權擬合直線方程法的原理

加權擬合直線方程法的數學模型^[1]

加權擬合直線方程法案例分析

案例一:加權擬合直線方程法在旅游需求預測中的應用^[1]

相關條目

參考文獻

温馨提示

本条目相关课程

本条目由以下用户参与贡献

評論(共0條)

導航

意见反馈

查看

工具▼

加權擬合直線方程法

出自 MBA智库百科(https://wiki.mbalib.com/)

目錄

加權擬合直線方程法的原理

加權擬合直線方程法的數學模型[1]

加權擬合直線方程法案例分析

案例一:加權擬合直線方程法在旅游需求預測中的應用[1]

相關條目

參考文獻

温馨提示

本條目相關文檔

本条目相关课程

本条目由以下用户参与贡献

評論(共0條)

導航

意见反馈

加權擬合直線方程法的數學模型^[1]

案例一:加權擬合直線方程法在旅游需求預測中的應用^[1]