加权拟合直线方程法

用手机看条目

出自 MBA智库百科(https://wiki.mbalib.com/)

加权拟合直线方程法的原理

　　加权拟合直线方程法是要数据资料要按照时间先后本着重近轻远的原则，对离差平方和进行赋权，然后再按最小二乘原理，使离差平方和达到最小，求出加权拟合直线方程的过程。

　　拟合直线方程法根据最小二乘原理，使观察值对于估计值的离差平方和 $Q=\sum(y_t-\overline{y})^2$ 达到最小，再应用数学上求偏导数并令之等于零的求极值方法计算待定参数a、b，然后建立直线方程并用来预测。但此法存在缺陷是在拟合直线过程，对时间序列数据不分远期或近期，都一视同仁，同等对待。然而，实际上往往近期的数据资料对预测值的影响比远期的数据资料要重要得多。因此，在市场预测的实践中，要按照时间先后本着重近轻远的原则，对离差平方和进行赋权，然后再按最小二乘原理，使离差平方和达到最小，求出加权拟合直线方程的过程，称为加权拟合直线方程法。

　　假设：由近及远的离差平方和的权重分别为： $a^0,a^1,a^2\ldots,a^{n-1}$ 其中0≤a＜l。当 $a 0 = 1$ 时，说明对最近期数据赋予最大权重为l，而后由近及远，按a比例递减。各期权数衰减速度取决于a的取值，a取值越大(越接近于1)，则衰减速度越慢；反之，a的取值越小(越接近于0)，则衰减速度越快。如a=1,则转化为如上述的非加权拟合直线方程法。

[编辑]

加权拟合直线方程法的数学模型^[1]

　　假设加权拟合直线方程为

　　 $\overline{y}_t=\overline{a}+\overline{b}x_1$

　　加权离差平方和为

　　 $Q=\sum_{t=1}^n a^{n-1}(y_t-\overline{a}-\overline{b}x_1)$ (1)

　　要使Q达到最小,应用多元函数求极值的方法,对(1)式分别求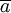 $\overline{a}$ 与 $\overline{b}$ 的偏导数。

　　 $\frac{\partial Q}{\partial\overline{a}}=-2[\sum_{t=1}^n a^{n-1}y_t-\overline{a}\sum_{t=1}^n a^{n-1}-\overline{b}\sum_{t=1}^n a^{n-1}x_1]$

　　 $\frac{\partial Q}{\partial\overline{b}}=-2[\sum_{t=1}^n a^{n-1}x_t y_t-\overline{a}\sum_{t=1}^n a^{n-1}x_t-\overline{b}\sum_{t=1}^n a^{n-1}x_t^2]$

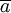　　并令 $\overline{a}$ 与 $\overline{b}$ 的偏导数均为0,即

　　 $\sum_{t=1}^n a^{n-1}y_t-\overline{a}\sum_{t=1}^n a^{n-1}-\overline{b}\sum_{t=1}^n a^{n-1}x_t$ 　　(2)

　　 $\sum_{t=1}^n a^{n-1}x_t y_t-\overline{a}\sum_{t=1}^n a^{n-1}x_t-\overline{b}\sum_{t=1}^n a^{n-1}x_t^2$ 　　(3)

　　对(2)(3)两式联立方程,进行求解,即可得到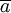 $\overline{a}$ 和 $\overline{b}$ 的值。

[编辑]

加权拟合直线方程法案例分析

[编辑]

案例一:加权拟合直线方程法在旅游需求预测中的应用^[1]

　　一、问题的提出

　　在旅游业比较发达的国家,计量经济学已应用到旅游经济研究之中.1961年,随着一篇名为《国际市场上旅游商品与服务的需求》的文章问世,旅游需求预测引起了人们的关注.1973年, Strazhein、Harrop等人应用旅游需求收入弹性和价格弹性解释了国际旅游需求的高速发展.1991年, Sung Soo Pyp在《旅游需求的线性消费模型》中成功地运用模型分析了价格、收入、时间等因素对旅游需求的影响.目前,国内对旅游需求预测并未引起学术界和旅游界人士的太多关注,相关文献不多。下面应用趋势外推预测法中的加权拟合直线方程法,对海外人士来哈尔滨旅游需求进行预测,并通过实际的旅游人数进行验证、探讨此方法的准确性、可行性。

　　二、加权拟合直线方程法

　　任何预测方法都是某种推测或推断,而对时间序列而言,推测与推断都是一种外推。趋势外推预测法是根据事物发展的特有规律,推测并着重研究其发展的可能趋势,并通过建立适当的预测模型,推断其未来变化的趋势。

　　趋势外推预测法的两个前提假设是:

　　假设一:技术或经济的发展因素,不但决定了过去的技术或经济的发展,而且在很大程度上也决定着该技术的未来发展.这一前提假设实质上,指的是在研究某项技术的过去、现在和未来的整个发展过程中,内外、因素保持相对不变.假设二:技术或经济的发展过程,一般属于渐进变化,而不是跳跃性变化。

　　趋势外推预测法分为拟合直线方程法和加权拟合直线方程法。在此我们采用加权拟合直线方程法进行旅游需求预测。

　　1)加权拟合直线方程法的原理

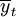　　预测的基本思想是使预测结果与实际数据的误差的平方和达到最小.误差平方和 $\sum_{t=1}^n(y_t-\overline{y}_t)^2$ 是每年旅游人数的实际值 $y t$ 与该年旅游人数的预测值 $\overline{y}_t$ 的偏差值的平方和,这就意味着∑ $\sum_{t=1}^n(y_t-\overline{y}_t)^2$ 中的每一项都有同样的重要性,即无论这个误差是近期的还是远期的,都赋予同等的权数.但实际上,对于预测精度来说,近期的误差比远期的误差更为重要.因此,在经济预测的实践中,要按时间先后,本着重近轻远的原则,对离差平方和进行赋权,然后再按最小二乘原理,使离差分平方和达到最小,求出加权拟合直线方程.这种方法称为加权拟合直线方程法。

　　二、对海外人士来哈尔滨旅游需求预测分析

　　以1996年至2001年海外人士来哈尔滨旅游人数作为观测值,对2002、2003年至2006年进行旅游需求预测,并与实际旅游人数做比较,分析、探讨.取a=0.5,分别计算各年的 $n-t,a^{n-1},y_t,a^{n-t}x_t y_t,a^{n-t}x_t,a^{n-t}x^2_t,$ 并列表如下表所示。

　　1996年至2001年海外来哈尔滨市旅游人数及加权拟合直线方程法计算表

年份	1996	1997	1998	1999	2000	2001	求和
$x t$	1	2	3	4	5	6
观测值 $y t$	5	4	3	2	1	0
$n - t$	0.03125	0.0625	0.125	0.25	0.5	1	1.96875
$a n - 1, y t$	3139.344	7524.188	16556.38	36151.5	77541.5	169722	310634.9
$a n - t x t y t$	3139.344	15048.38	49669.13	144606	387707.5	1018332	1618502
$a n - t x t$	0.03125	0.125	0.375	1	2.5	6	10.03125
$a^{n-t}x^2_t$	0.03125	0.25	0.125	4	12.5	36	53.90625

　　确定待定系数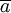 $\overline{a}$ 和 $\overline{b}$ ,建立预测模型 $\overline{y}_t=\overline{a}+\overline{b}x_1$ 。

　　由(2)(3)及表1可知

　　 $\begin{cases}310634.9-1.96875\overline{a}-10.03125\overline{b}=0\\1618502-10.03125\overline{a}-53.90625\overline{b}=0\end{cases}$

　　联立解方程组,求解得 $\overline{a}\approx92614.62,\overline{b}\approx12790$ 。故预测模型为

　　 $\overline{y}=92614.62+12790x_t$

　　用此模型求2002、2003至2006年的预测值

　　当 $x t = 7$ 时, $\overline{y}_2002=92614.62+12790\times7=182144.6$ 即预测2002年海外来哈旅游人数约为182144.6人.下面列出由此预测模型计算出的预测值与实际旅游人数相对照。

　　1996年至2006年海外来哈尔滨市旅游人数预测值与实际旅游人数对照表

年份	1996	1997	1998	1999	2000	2001	2002	2003	2004	2005	2006
预测值	105405	118195	130985	143775	156565	169355	182145	194935	207725	220515	233305
实际值	100459	120387	132451	144606	155083	169722	184253	145538	183818	203901	237498

　　由上表我们看到1996~2001拟合的效果非常好。2002的预测准确率比较高,而2003准确率极低,2004、2005准确率也不高。但是2006预测准确率又比较高.我们反思2003年就不足为奇了。2003年是非典时期,它严重影响、干扰了旅游业的发展,因而出现了较大的跳动。为了探讨加权拟合直线方程法在旅游需求预测中的有效性。不妨以这一时期开始的实际数据作为观测值,进行下一个预测。即以2003年~2006年海外人士来哈尔滨旅游人数作为观测值,对2007年至2008年进行旅游需求预测。

　　仍取a=0.5,分别计算各年的 $n-t,a^{n-1},y_t,a^{n-t}x_t y_t,a^{n-t}x_t,a^{n-t}x^2_t,$ 并列表如下表所示。

　　2003年至2006年海外来哈尔滨市旅游人数及加权拟合直线方程法计算表

年份	2003	2004	2005	2006	求和
$x t$	1	2	3	4
观测值 $y t$	145538	183818	203901	237498
$n - t$	3	2	1	0
$a n - 1$	0.125	0.25	0.5	1	1.875
$a n - 1, y t$	18192.25	45954.5	101950.5	237498	403595.3
$a n - t x t \| \| y t$	18192.25	91909	305851.5	949992	1365945
$a n - t x t$	0.125	0.5	1.5	4	6.125
$a^{n-t}x^2_t$	0.125	1	4.5	16	21.625

　　确定待定系数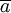 $\overline{a}$ 和 $\overline{b}$ ,建立预测模型。由(2)(3)及上表可知

　　 $\begin{cases}403595.3-1.875\overline{a}-6.125\overline{b}=0\\1365945-6.125\overline{a}-21.625\overline{b}=0\end{cases}$

　　联立求解得 $\overline{a}\approx119203.4,\overline{b}\approx29402.28$ 。故预测模型为

　　 $\overline{y}=119203.4+29402.28x_t$

　　预测2007、2008年的旅游人数为

　　当 $x t = 5$ 时, $\overline{y}_2007=119203.4+29402.28\times5=266214.8$

　　当 $x t = 6$ 时 $\overline{y}_2008=119203.4+29402.28\times6=295617.08$

　　列出由此预测模型计算出的预测值与实际旅游人数相对照。

　　2003年至2008年海外来哈尔滨市旅游人数预测值与实际旅游人数对照表

年份	2003	2004	2005	2006	2007	2008
预测值	148605.7	178008	207410.2	236812.5	266214.8	295617.1
实际值	145538	183818	203901	237498	269628

　　由此我们看到以2003年~2006年旅游人数作为观测值,预测2007年旅游人数准确率是比较高的.误差不超过2%.2008年的旅游人数预测已经得出。这还要2008年末实际旅游人数来考证.我们将拭目以待。通过旅游人数的预测,我们也看到,抛开非典特殊时期,总体来说,哈尔滨旅游业的发展是比较平稳的。逐年呈线性上升趋势。

　　通过上述海外来哈尔滨旅游人数预测值与实际旅游人数对比,能够体现出加权拟合直线法在实际应用过程中具有较好的的准确率。其数学模型简单,计算方法简便、易行.易于旅游界人士操作.但是值得强调的是,应用加权拟合直线法进行旅游需求预测前提,必须是旅游业的平稳发展.如果有一些干扰因素.那末在预测时,必须综合分析。

[编辑]

参考文献

↑ ^1.0 ^1.1 孙伟.加权拟合直线方程法在旅游需求预测中的应用[J].数学的实践与认识,2009,39(2)

来自"https://wiki.mbalib.com/wiki/%E5%8A%A0%E6%9D%83%E6%8B%9F%E5%90%88%E7%9B%B4%E7%BA%BF%E6%96%B9%E7%A8%8B%E6%B3%95"

打开MBA智库App, 阅读完整内容打开App

如果您认为本条目还有待完善，需要补充新内容或修改错误内容，请编辑条目或投诉举报。

本条目由以下用户参与贡献

Yixi,Tiffany,HEHE林,KAER.

页面分类: 统计方法

评论(共0条)

提示:评论内容为网友针对条目"加权拟合直线方程法"展开的讨论，与本站观点立场无关。

发表评论请文明上网，理性发言并遵守有关规定。

查看

工具箱▼

加权拟合直线方程法

出自 MBA智库百科(https://wiki.mbalib.com/)

目录

加权拟合直线方程法的原理

加权拟合直线方程法的数学模型^[1]

加权拟合直线方程法案例分析

案例一:加权拟合直线方程法在旅游需求预测中的应用^[1]

相关条目

参考文献

温馨提示

本条目相关课程

本条目由以下用户参与贡献

评论(共0条)

导航

意见反馈

查看

工具箱▼

加权拟合直线方程法

出自 MBA智库百科(https://wiki.mbalib.com/)

目录

加权拟合直线方程法的原理

加权拟合直线方程法的数学模型[1]

加权拟合直线方程法案例分析

案例一:加权拟合直线方程法在旅游需求预测中的应用[1]

相关条目

参考文献

温馨提示

本条目相关文档

本条目相关课程

本条目由以下用户参与贡献

评论(共0条)

导航

意见反馈

加权拟合直线方程法的数学模型^[1]

案例一:加权拟合直线方程法在旅游需求预测中的应用^[1]