预测精度
用手机看条目
出自 MBA智库百科(https://wiki.mbalib.com/)
预测精度(Forecast Accuracy)
目录 |
[编辑]
预测精度是指预测模型拟合的好坏程度，即由预测模型所产生的模拟值与历史实际值拟合程度的优劣。预测精度是衡量预测方法是否适用于预测对象的一个重要指标。
[编辑]
- 预测方法选取的合理性
- 所建模型的正确性
- 资料的准确和全面性
- 预测者的素质
[编辑]
一、平均误差和平均绝对误差
平均误差的公式为:
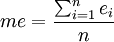
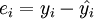
平均绝对误差的公式为：
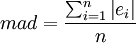
二、平均相对误差和平均相对误差绝对值
平均相对误差的公式为：
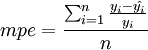
平均相对误差绝对值的公式为：
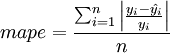
预测误差的方差公式为：
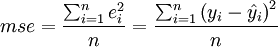
预测误差的标准差公式为：
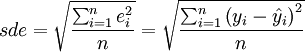
预测误差的方差比平均绝对误差或平均相对误差绝对值能更好地衡量预测的精确度。
[编辑]
- 符合经济规律和经济特点
- 符合统计资料反映的规律
- 力求取得较好的预测精确度
- 力求实用
[编辑]
3.常用定量预测方法的评价
大型模型的预测精度并不比小模型的预测精度高；没有任何一种预测方法或预测模型会在各种情况下都比其他方法或模型表现得更好；大型的回归模型能提供更多的有关影响预测对象的变化的因素的信息，能够更好地解释预测对象变化的原因。所以，如果用户选择预测方法的标准是追求预测精度的极大化，则最好选择时间序列预测模型，如果预测精度只是选择预测方法的重要标准之一，则可以考虑选择小型的回归模型。
ok!