二次指數平滑法

用手机看条目

出自 MBA智库百科(https://wiki.mbalib.com/)

二次指數平滑法（Second exponential smoothing method）

什麼是二次指數平滑法

　　二次指數平滑法是對一次指數平滑值作再一次指數平滑的方法。它不能單獨地進行預測，必須與一次指數平滑法配合，建立預測的數學模型，然後運用數學模型確定預測值。一次移動平均法的兩個限制因素線上性二次移動平均法中也才存在，線性二次指數，平滑法只利用三個數據和一個α值就可進行計算；在大多數情況下，一般更喜歡用線性二次指數平滑法作為預測方法。

[編輯]

二次指數平滑法的優點^[1]

　　二次指數平滑法實質上是將歷史數據進行加權平均作為未來時刻的預測結果。

　　它具有計算簡單、樣本要求量較少、適應性較強、結果較穩定。

[編輯]

二次指數平滑法的計算

　　線性二次指數平滑法的公式為：

　　 $S^{(2)}_{t}=aS^{(1)}_t+(1-a)S_{t-1}^{(2)}$ 　　(1)

式中： $S^{(2)}_{t},S^{(2)}_{t-1}$ 分別為t期和t–1期的二次指數平滑值；a為平滑繫數。在 $S^{(1)}_{t}$ 和 $S^{(2)}_{t}$ 已知的條件下，二次指數平滑法的預測模型為：

　　 $\hat{Y}_{t+T}=a_t+b_t\cdot T$ 　　(2)

　　 $S_{t}^{(2)}=aS^{(1)}_{t}+(1-a)S^{(2)}_{t-1}$

　　 $\begin{cases}a_t=2S^{(1)}_{t}-S^{(2)}_t\\b_t=\frac{a}{1-a}\left(S^{(1)}_t-S^{(2)}_t\right)\end{cases}$ 　　(3)

　　T為預測超前期數

例5：某地1983年至1993年財政入的資料如下，試用指數平滑法求解趨勢直線方程並預測1996年的財政收入。計算過程及結果如下：

年份	t	財政收入（元）	$S^{(1)}_{t}=aY_t+(1-a)S_{t-1}^{(1)}$ a=0.9　初始值為23	$S_{t}^{(2)}=aS^{(1)}_{t}+(1-a)S^{(2)}_{t-1}$ a=0.9　初始值為28.40
1983	1	29	28.40
1984	2	36	35.24	34.56
1985	3	40	39.52	39.02
1986	4	48	47.15	46.14
1987	5	54	53.32	52.62
1988	6	62	61.13	60.28
1989	7	70	69.0	68.23
1990	8	76	75.31	74.60
1991	9	85	84.03	83.09
1992	10	94	93.00	92.01
1993	11	103	102.00	101.00

由上表可知： $S^{(1)}_0=23$ ； $S^{(1)}_{11}=102$ ； $S^{(2)}_0=28.4$ ； $S^{(2)}_{11}=101$ ,a=0.9 則

　　 $a_1=2S^{(1)}_{t}-S^{(2)}_{t} a_{11}=2\times S^{(1)}_{11}-S^{(2)}_{11}=2\times102=103$

　　 $b_t=\frac{a}{1-a}(S^{(1)}_t-S^{(2)}_t) b_{11}=\frac{0.9}{1-0.9}(102-101)=9$ 所求模型為:

　　 $Y_{11+T}=103+9\cdot T$

　　1996年該地區財政收入預測值為: $Y_{11+3}=103+9\times 3=130$ (萬元)

[編輯]

二次指數平滑法實例分析^[2]

　　表中第③欄是我國1978-2002年全社會客運量的資料,據期繪製散點圖，見下圖，可以看出，各年的客運量資料基本呈線性趨勢，但在幾個不同的時期直線有不同的斜率，因此考慮用變參數線性趨勢模型進行預測。具體步驟如下：

　　表我國1978-2002年全社會客運量及預測值單位：萬人

年份	時間t	全社會客運量y	各期的一次指數平滑值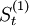 $S_t^{(1)}$	各期的二次指數平滑值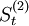 $S_t^{(2)}$	$a t$	$b t$	$\widehat{y}_{t+1}=a_t+b_t$
①	②	③	④	⑤	⑥	⑦	⑧
			253993.0	253993.0
1978	1	253993	253993.0	253993.0	253993.0	0.0
1979	2	289665	275396.2	266834.9	283957.5	12841.9	253993.0
1980	3	341785	315229.5	295871.7	334587.3	29036.7	296799.4
1981	4	384763	356949.6	332518.4	381380.8	36646.8	363624.0
1982	5	428964	400158.2	373102.3	427214.2	40583.9	418027.5
1983	6	470614	442431.7	414699.9	470163.4	41597.6	467798.1
1984	7	530217	495102.9	462941.7	527264.1	48241.8	511761.1
1985	8	620206	570164.8	527275.5	613054.0	64333.8	575505.8
1986	9	688212	640993.1	595506.1	686480.1	68230.5	677387.8
1987	10	746422	704250.4	660752.7	747748.2	65246.6	754710.7
1988	11	809592	767455.4	724774.3	810136.4	64021.6	812994.8
1989	12	791376	781807.8	758994.4	804621.1	34220.1	874158.1
1990	13	772682	776332.3	769397.1	783267.5	10402.8	838841.2
1991	14	806048	794161.7	784255.9	804067.6	14858.8	793670.2
1992	15	860855	834177.7	814209.0	854146.4	29953.1	818926.3
1993	16	996630	931651.5	884674.5	978628.5	70465.5	884099.5
1994	17	1092883	1028390.4	970904.0	1085876.8	86229.6	1049094.0
1995	18	1172596	1114913.8	1057309.9	1172517.6	86405.8	1172106.3
1996	19	1245356	1193179.1	1138831.4	1247526.8	81521.5	1258923.5
1997	20	1326094	1272928.0	1219289.4	1326566.7	80458.0	1329048.3
1998	21	1378717	1336401.4	1289556.6	1383246.2	70267.2	1407024.7
1999	22	1394413	1371208.4	1338547.7	1403869.1	48991.1	1453513.4
2000	23	1478573	1435627.1	1396795.4	1474458.9	58247.7	1452860.1
2001	24	1534122	1494724.1	1455552.6	1533895.5	58757.2	1532706.6
2002	25	1608150	1562779.6	1519888.8	1605670.4	64336.2	1592652.8
2003	26						1670006.7
2004	27						1734342.9

　　第一步，計算一次指數平滑值。取 $a=0.6,S_0^{(2)}=S_0^{(1)}=y_1=253993$ ，根據一次指數平滑公式 $S^{(1)}=ay+(1-a)S_{-1}^{(1)}$ ，可計算各期的一次指數平滑預測值：

　　1978年： $S_1^{(1)}=06\times y_1+0.4\times S_0^{(1)}=0.6\times253993+0.4\times253993=253993$

　　1979年： $S_2^{(1)}=06\times y_2+0.4\times S_1^{(1)}=0.6\times289665+0.4\times253993=275396.2$

　　同理可得各年的一次指數平滑預測值，見表1中第④欄。

　　第二步，根據（1）式和第一步計算的，計算各期的二次指數平滑值，見表1中第⑤欄。如：

　　 $S_1^{(2)}=0.6\times S_1^{(1)}+0.4\times S_0^{(2)}=0.6\times253993+0.4\times253993=253993$

　　 $S_2^{(2)}=0.6\times S_2^{(1)}+0.4\times S_1^{(2)}=0.6\times275396+0.4\times253993=266834.9$

　　其餘各期以此類推。

　　第三步，計算各期參數變數值α、b。根據（3）式，可計算各期的α、b，分別見表第⑥、第⑦欄。如

　　 $\begin{cases}a_2-2S_2^(1)-S_2(2)=2\times275396.2-266834.9=283957.5\\b_2=\frac{a}{1-a}(S_2^(1)-S_2(2))=\frac{0.6}{0.4}(275396.2-266834.9)=12841.9\end{cases}$

　　第四步，根據（4）式和（2）式分別求各期的趨勢預測值，見表中最後一欄。如：

　　2000年預測值 $\widehat{y}_23=\widehat{y}_{22+1}=a_{22}+(b_{22})\times1=1403869.1+148991.1=1452860$ ；

　　進行外推預測,則

　　2003年預測值 $\widehat{y}_26=\widehat{y}_{25+1}=a_{25}+(b_{25})\times1=1605670.4+64336.2=1670006.7$ ；

　　2004年預測值 $\widehat{y}_{27}=\widehat{y}_{26+1}=a_(25)+(b_{25})\times1=1605670.4+64336.2\times2=1734342.9$ 。

　　把各年的預測值繪成曲線與原時間序列的散點圖比較（見上圖），可以看出，二次指數平滑法由於考慮了時間序列在不同時期直線參數的變化，其預測值與原時間序列的擬合程度非常好。上圖中也給出了用最小二乘法擬合的趨勢直線，相比之下，用二次指數平滑法擬合的趨勢線更好地體現了原時間序列在不同時間段的變化趨勢。

[編輯]

參考文獻

↑ 米翠蘭.二次指數平滑法的研究與應用[J].華北煤炭醫學院學報.2000(5)
↑ 二次指數平滑法的應用.莊贇.

取自"https://wiki.mbalib.com/zh-tw/%E4%BA%8C%E6%AC%A1%E6%8C%87%E6%95%B0%E5%B9%B3%E6%BB%91%E6%B3%95"

打开MBA智库App, 阅读完整内容打开App

如果您認為本條目還有待完善，需要補充新內容或修改錯誤內容，請編輯條目或投訴舉報。

本条目由以下用户参与贡献

Kuxiaoxue,Vulture,Angle Roh,冬阳,Dan,Xiangtaiyan,Yixi,寒曦,Tracy,John DHH,飞舞的哲.

頁面分類: 決策預測

評論(共13條)

提示:評論內容為網友針對條目"二次指數平滑法"展開的討論，與本站觀點立場無關。

202.105.64.* 在 2008年7月15日 22:15 發表

線性二次指數平滑法的公式錯了！不過表格裡的式子是對的。。。

回複評論

125.38.9.* 在 2009年1月7日 00:25 發表

那裡錯了？說明白呀！

回複評論

Angle Roh (討論 | 貢獻) 在 2009年1月7日 13:27 發表

125.38.9.* 在 2009年1月7日 00:25 發表

那裡錯了？說明白呀！

原公式錯誤之處，已有網友做了修改，您可以查看一下歷史版本，便於分析

回複評論

218.19.68.* 在 2009年2月17日 10:44 發表

這裡的初始值怎麼確定的啊？是資料中給的嗎

回複評論

114.255.18.* 在 2009年6月11日 09:47 發表

初始值23是怎麼得出來的？

回複評論

121.15.226.* 在 2011年3月14日 16:51 發表

114.255.18.* 在 2009年6月11日 09:47 發表

初始值23是怎麼得出來的？

回複評論

Yixi (討論 | 貢獻) 在 2011年3月15日 13:33 發表

121.15.226.* 在 2011年3月14日 16:51 發表

初始值23是怎麼得出來的？

增加了新的內容，希望對您有幫助！

回複評論

222.243.123.* 在 2013年4月21日 21:31 發表

t和T怎麼確定？

回複評論

222.18.60.* 在 2013年8月31日 14:18 發表

很有用

回複評論

171.39.165.* 在 2017年3月16日 09:58 發表

平滑繫數是怎麼得到的

回複評論

125.76.163.* 在 2018年6月27日 17:55 發表

23的初始值，怎麼的出來的

回複評論

163.244.246.* 在 2020年1月5日 22:59 發表

初始值比較隨意

回複評論

117.157.80.* 在 2020年6月27日 09:46 發表

廚師長

回複評論

發表評論請文明上網，理性發言並遵守有關規定。

查看

工具▼

二次指數平滑法

出自 MBA智库百科(https://wiki.mbalib.com/)

目錄

什麼是二次指數平滑法

二次指數平滑法的優點^[1]

二次指數平滑法的計算

二次指數平滑法實例分析^[2]

參考文獻

温馨提示

本条目相关课程

本条目由以下用户参与贡献

評論(共13條)

導航

意见反馈

查看

工具▼

二次指數平滑法

出自 MBA智库百科(https://wiki.mbalib.com/)

目錄

什麼是二次指數平滑法

二次指數平滑法的優點[1]

二次指數平滑法的計算

二次指數平滑法實例分析[2]

參考文獻

温馨提示

本條目相關文檔

本条目相关课程

本条目由以下用户参与贡献

評論(共13條)

導航

意见反馈

二次指數平滑法的優點^[1]

二次指數平滑法實例分析^[2]