二次指数平滑法

用手机看条目

出自 MBA智库百科(https://wiki.mbalib.com/)

二次指数平滑法（Second exponential smoothing method）

什么是二次指数平滑法

　　二次指数平滑法是对一次指数平滑值作再一次指数平滑的方法。它不能单独地进行预测，必须与一次指数平滑法配合，建立预测的数学模型，然后运用数学模型确定预测值。一次移动平均法的两个限制因素在线性二次移动平均法中也才存在，线性二次指数，平滑法只利用三个数据和一个α值就可进行计算；在大多数情况下，一般更喜欢用线性二次指数平滑法作为预测方法。

[编辑]

二次指数平滑法的优点^[1]

　　二次指数平滑法实质上是将历史数据进行加权平均作为未来时刻的预测结果。

　　它具有计算简单、样本要求量较少、适应性较强、结果较稳定。

[编辑]

二次指数平滑法的计算

　　线性二次指数平滑法的公式为：

　　 $S^{(2)}_{t}=aS^{(1)}_t+(1-a)S_{t-1}^{(2)}$ 　　(1)

式中： $S^{(2)}_{t},S^{(2)}_{t-1}$ 分别为t期和t–1期的二次指数平滑值；a为平滑系数。在 $S^{(1)}_{t}$ 和 $S^{(2)}_{t}$ 已知的条件下，二次指数平滑法的预测模型为：

　　 $\hat{Y}_{t+T}=a_t+b_t\cdot T$ 　　(2)

　　 $S_{t}^{(2)}=aS^{(1)}_{t}+(1-a)S^{(2)}_{t-1}$

　　 $\begin{cases}a_t=2S^{(1)}_{t}-S^{(2)}_t\\b_t=\frac{a}{1-a}\left(S^{(1)}_t-S^{(2)}_t\right)\end{cases}$ 　　(3)

　　T为预测超前期数

例5：某地1983年至1993年财政入的资料如下，试用指数平滑法求解趋势直线方程并预测1996年的财政收入。计算过程及结果如下：

年份	t	财政收入（元）	$S^{(1)}_{t}=aY_t+(1-a)S_{t-1}^{(1)}$ a=0.9　初始值为23	$S_{t}^{(2)}=aS^{(1)}_{t}+(1-a)S^{(2)}_{t-1}$ a=0.9　初始值为28.40
1983	1	29	28.40
1984	2	36	35.24	34.56
1985	3	40	39.52	39.02
1986	4	48	47.15	46.14
1987	5	54	53.32	52.62
1988	6	62	61.13	60.28
1989	7	70	69.0	68.23
1990	8	76	75.31	74.60
1991	9	85	84.03	83.09
1992	10	94	93.00	92.01
1993	11	103	102.00	101.00

由上表可知： $S^{(1)}_0=23$ ； $S^{(1)}_{11}=102$ ； $S^{(2)}_0=28.4$ ； $S^{(2)}_{11}=101$ ,a=0.9 则

　　 $a_1=2S^{(1)}_{t}-S^{(2)}_{t} a_{11}=2\times S^{(1)}_{11}-S^{(2)}_{11}=2\times102=103$

　　 $b_t=\frac{a}{1-a}(S^{(1)}_t-S^{(2)}_t) b_{11}=\frac{0.9}{1-0.9}(102-101)=9$ 所求模型为:

　　 $Y_{11+T}=103+9\cdot T$

　　1996年该地区财政收入预测值为: $Y_{11+3}=103+9\times 3=130$ (万元)

[编辑]

二次指数平滑法实例分析^[2]

　　表中第③栏是我国1978-2002年全社会客运量的资料,据期绘制散点图，见下图，可以看出，各年的客运量资料基本呈线性趋势，但在几个不同的时期直线有不同的斜率，因此考虑用变参数线性趋势模型进行预测。具体步骤如下：

　　表我国1978-2002年全社会客运量及预测值单位：万人

年份	时间t	全社会客运量y	各期的一次指数平滑值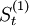 $S_t^{(1)}$	各期的二次指数平滑值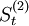 $S_t^{(2)}$	$a t$	$b t$	$\widehat{y}_{t+1}=a_t+b_t$
①	②	③	④	⑤	⑥	⑦	⑧
			253993.0	253993.0
1978	1	253993	253993.0	253993.0	253993.0	0.0
1979	2	289665	275396.2	266834.9	283957.5	12841.9	253993.0
1980	3	341785	315229.5	295871.7	334587.3	29036.7	296799.4
1981	4	384763	356949.6	332518.4	381380.8	36646.8	363624.0
1982	5	428964	400158.2	373102.3	427214.2	40583.9	418027.5
1983	6	470614	442431.7	414699.9	470163.4	41597.6	467798.1
1984	7	530217	495102.9	462941.7	527264.1	48241.8	511761.1
1985	8	620206	570164.8	527275.5	613054.0	64333.8	575505.8
1986	9	688212	640993.1	595506.1	686480.1	68230.5	677387.8
1987	10	746422	704250.4	660752.7	747748.2	65246.6	754710.7
1988	11	809592	767455.4	724774.3	810136.4	64021.6	812994.8
1989	12	791376	781807.8	758994.4	804621.1	34220.1	874158.1
1990	13	772682	776332.3	769397.1	783267.5	10402.8	838841.2
1991	14	806048	794161.7	784255.9	804067.6	14858.8	793670.2
1992	15	860855	834177.7	814209.0	854146.4	29953.1	818926.3
1993	16	996630	931651.5	884674.5	978628.5	70465.5	884099.5
1994	17	1092883	1028390.4	970904.0	1085876.8	86229.6	1049094.0
1995	18	1172596	1114913.8	1057309.9	1172517.6	86405.8	1172106.3
1996	19	1245356	1193179.1	1138831.4	1247526.8	81521.5	1258923.5
1997	20	1326094	1272928.0	1219289.4	1326566.7	80458.0	1329048.3
1998	21	1378717	1336401.4	1289556.6	1383246.2	70267.2	1407024.7
1999	22	1394413	1371208.4	1338547.7	1403869.1	48991.1	1453513.4
2000	23	1478573	1435627.1	1396795.4	1474458.9	58247.7	1452860.1
2001	24	1534122	1494724.1	1455552.6	1533895.5	58757.2	1532706.6
2002	25	1608150	1562779.6	1519888.8	1605670.4	64336.2	1592652.8
2003	26						1670006.7
2004	27						1734342.9

　　第一步，计算一次指数平滑值。取 $a=0.6,S_0^{(2)}=S_0^{(1)}=y_1=253993$ ，根据一次指数平滑公式 $S^{(1)}=ay+(1-a)S_{-1}^{(1)}$ ，可计算各期的一次指数平滑预测值：

　　1978年： $S_1^{(1)}=06\times y_1+0.4\times S_0^{(1)}=0.6\times253993+0.4\times253993=253993$

　　1979年： $S_2^{(1)}=06\times y_2+0.4\times S_1^{(1)}=0.6\times289665+0.4\times253993=275396.2$

　　同理可得各年的一次指数平滑预测值，见表1中第④栏。

　　第二步，根据（1）式和第一步计算的，计算各期的二次指数平滑值，见表1中第⑤栏。如：

　　 $S_1^{(2)}=0.6\times S_1^{(1)}+0.4\times S_0^{(2)}=0.6\times253993+0.4\times253993=253993$

　　 $S_2^{(2)}=0.6\times S_2^{(1)}+0.4\times S_1^{(2)}=0.6\times275396+0.4\times253993=266834.9$

　　其余各期以此类推。

　　第三步，计算各期参数变量值α、b。根据（3）式，可计算各期的α、b，分别见表第⑥、第⑦栏。如

　　 $\begin{cases}a_2-2S_2^(1)-S_2(2)=2\times275396.2-266834.9=283957.5\\b_2=\frac{a}{1-a}(S_2^(1)-S_2(2))=\frac{0.6}{0.4}(275396.2-266834.9)=12841.9\end{cases}$

　　第四步，根据（4）式和（2）式分别求各期的趋势预测值，见表中最后一栏。如：

　　2000年预测值 $\widehat{y}_23=\widehat{y}_{22+1}=a_{22}+(b_{22})\times1=1403869.1+148991.1=1452860$ ；

　　进行外推预测,则

　　2003年预测值 $\widehat{y}_26=\widehat{y}_{25+1}=a_{25}+(b_{25})\times1=1605670.4+64336.2=1670006.7$ ；

　　2004年预测值 $\widehat{y}_{27}=\widehat{y}_{26+1}=a_(25)+(b_{25})\times1=1605670.4+64336.2\times2=1734342.9$ 。

　　把各年的预测值绘成曲线与原时间序列的散点图比较（见上图），可以看出，二次指数平滑法由于考虑了时间序列在不同时期直线参数的变化，其预测值与原时间序列的拟合程度非常好。上图中也给出了用最小二乘法拟合的趋势直线，相比之下，用二次指数平滑法拟合的趋势线更好地体现了原时间序列在不同时间段的变化趋势。

[编辑]

参考文献

↑ 米翠兰.二次指数平滑法的研究与应用[J].华北煤炭医学院学报.2000(5)
↑ 二次指数平滑法的应用.庄赟.

来自"https://wiki.mbalib.com/wiki/%E4%BA%8C%E6%AC%A1%E6%8C%87%E6%95%B0%E5%B9%B3%E6%BB%91%E6%B3%95"

打开MBA智库App, 阅读完整内容打开App

如果您认为本条目还有待完善，需要补充新内容或修改错误内容，请编辑条目或投诉举报。

本条目由以下用户参与贡献

Kuxiaoxue,Vulture,Angle Roh,冬阳,Dan,Xiangtaiyan,Yixi,寒曦,Tracy,John DHH,飞舞的哲.

页面分类: 决策预测

评论(共13条)

提示:评论内容为网友针对条目"二次指数平滑法"展开的讨论，与本站观点立场无关。

202.105.64.* 在 2008年7月15日 22:15 发表

线性二次指数平滑法的公式错了！不过表格里的式子是对的。。。

回复评论

125.38.9.* 在 2009年1月7日 00:25 发表

那里错了？说明白呀！

回复评论

Angle Roh (Talk | 贡献) 在 2009年1月7日 13:27 发表

125.38.9.* 在 2009年1月7日 00:25 发表

那里错了？说明白呀！

原公式错误之处，已有网友做了修改，您可以查看一下历史版本，便于分析

回复评论

218.19.68.* 在 2009年2月17日 10:44 发表

这里的初始值怎么确定的啊？是资料中给的吗

回复评论

114.255.18.* 在 2009年6月11日 09:47 发表

初始值23是怎么得出来的？

回复评论

121.15.226.* 在 2011年3月14日 16:51 发表

114.255.18.* 在 2009年6月11日 09:47 发表

初始值23是怎么得出来的？

初始值23是怎麼得出來的？

回复评论

Yixi (Talk | 贡献) 在 2011年3月15日 13:33 发表

121.15.226.* 在 2011年3月14日 16:51 发表

初始值23是怎麼得出來的？

增加了新的内容，希望对您有帮助！

回复评论

222.243.123.* 在 2013年4月21日 21:31 发表

t和T怎么确定？

回复评论

222.18.60.* 在 2013年8月31日 14:18 发表

很有用

回复评论

171.39.165.* 在 2017年3月16日 09:58 发表

平滑系数是怎么得到的

回复评论

125.76.163.* 在 2018年6月27日 17:55 发表

23的初始值，怎么的出来的

回复评论

163.244.246.* 在 2020年1月5日 22:59 发表

初始值比较随意

回复评论

117.157.80.* 在 2020年6月27日 09:46 发表

厨师长

回复评论

发表评论请文明上网，理性发言并遵守有关规定。

查看

工具箱▼

二次指数平滑法

出自 MBA智库百科(https://wiki.mbalib.com/)

目录

什么是二次指数平滑法

二次指数平滑法的优点^[1]

二次指数平滑法的计算

二次指数平滑法实例分析^[2]

参考文献

温馨提示

本条目相关课程

本条目由以下用户参与贡献

评论(共13条)

导航

意见反馈

查看

工具箱▼

二次指数平滑法

出自 MBA智库百科(https://wiki.mbalib.com/)

目录

什么是二次指数平滑法

二次指数平滑法的优点[1]

二次指数平滑法的计算

二次指数平滑法实例分析[2]

参考文献

温馨提示

本条目相关文档

本条目相关课程

本条目由以下用户参与贡献

评论(共13条)

导航

意见反馈

二次指数平滑法的优点^[1]

二次指数平滑法实例分析^[2]