一次指數平滑法
出自 MBA智库百科(https://wiki.mbalib.com/)
一次指數平滑法(Single exponential smoothing)
目錄 |
一次指數平滑法是指以最後的一個第一次指數平滑。如果為了使指數平滑值敏感地反映最新觀察值的變化，應取較大阿爾法值，如果所求指數平滑值是用來代表該時間序列的長期趨勢值，則應取較小阿爾法值。同時，對於市場預測來說，還應根據中長期趨勢變動和季節性變動情況的不同而取不同的阿爾法值，一般來說，應按以下情況處理：
1.如果觀察值的長期趨勢變動接近穩定的常數，應取居中阿爾法值(一般取0.6—0.4)使觀察值在指數平滑中具有大小接近的權數；
2.如果觀察值呈現明顯的季節性變動時，則宜取較大的阿爾法值(一般取0.6一0.9)，使近期觀察在指數平滑值中具有較大作用，從而使近期觀察值能迅速反映在未來的預測值中；
3.如果觀察值的長期趨勢變動較緩慢，則宜取較小的e值(一般取0.1—0.4)，使遠期觀察值的特征也能反映在指數平滑值中。在確定預測值時，還應加以修正，在指數平滑值S，的基礎上再加一個趨勢值b，因而，原來指數平滑公式也應加一個b。
一次指數平滑法是根據前期的實測數和預測數，以加權因數為權數，進行加權平均，來預測未來時間趨勢的方法。
一次指數平滑法計算公式為：
yt + 1 = axt + (1 − a)yt
式中， xt―― 時期 t 的實測值；
yt―― 時期 t 的預測值；
a―― 平滑繫數，又稱加權因數，取值範圍為0≤a≤1。
將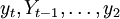
的表達式逐次代入yt + 1中，展開整理後，得：
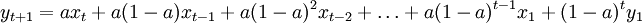
從上式中可以看出，一次指數平滑法實際上是以a(1 − a)k為權數的加權移動平均法。由於k越大，a(1 − a)k越小，所以越是遠期的實測值對未來時期平滑值的影響就越小。 在展開式中，最後一項y1為初始平滑值，在通常情況下可用最初幾個實測值的平均值來代替，或直接可用第 1 時期的實測值來代替。
從上式可以看出，新預測值是根據預測誤差對原預測值進行修正得到的。a的大小表明瞭修正的幅度。a值愈大，修正的幅度愈大，a值愈小，修正的幅度愈小。 因此，a值既代表了預測模型對時間序列數據變化的反應速度，又體現了預測模型修勻誤差的能力。
在實際應用中，a值是根據時間序列的變化特性來選取的。 若時間序列的波動不大，比較平穩，則a應取小一些，如0.1 ～ 0.3 ；若時間序列具有迅速且明顯的變動傾向， 則a應取大一些，如 0.6 ～ 0.9 。實質上，aa是一個經驗數據，通過多個值進行試算比較而定，哪個a值引起的預測誤差小，就採用哪個。
1、取第一期的實際值為初值；
2、取最初幾期的平均值為初值。
一次指數平滑法比較簡單，但也有問題。問題之一便是力圖找到最佳的α值，以使均方差最小，這需要通過反覆試驗確定。
評論(共2條)
//Swift version func forecastS1(input x:[Double],weight a:Double)->Double{ var count = Double(x.count)
return x[0..<x.count].reduce(0.0){ defer{ count -= 1 } return $0 + $1 * a * pow(1-a, count-1) } + pow(1-a, Double(x.count)) * x[0] }
simple exponential smoothing is the time serious method most frequently used for demand forecasting . it also smooth out the blips in the data ,but it's power over the n period is three fold , 1) old data never dropped 2. old data are given progressively lees weight , 3. the caculation is simple and only require the most recent data.