包絡曲線
出自 MBA智库百科(https://wiki.mbalib.com/)
包絡曲線(Envelop curve)
目錄 |
包絡曲線(Envelop curve)是由所有短期成本曲線(總成本曲線和平均成本曲線)最低點軌跡構成的相應的長期成本曲線。
雅各布·瓦伊納(Jacob Viner)在研究成本理論時,他提出了今天人們都熟悉的包絡曲線概念,即長期平均成本曲線是無數條短期平均成本曲線的包絡曲線。當時瓦伊納認為,在長期中企業總可以通過調整生產規模實現平均成本最低,因此,長期平均成本曲線應該是無數條短期平均成本曲線最低點組成的軌跡。
包絡曲線概述[1]
包絡曲線是西方經濟學中一個基本概念,也是分析長期成本的一種方法。作為重要的長期成本的分析工具之一,只有正確的理解了包絡曲線的真正含義,在運用包絡曲線的時候才會恰如其分、得心應手。為了理解包絡曲線,首先要清楚一定的前提。從時間的角度看,廠商在成本分析中有短期和長期之分,劃分的標準是廠商能否全部調整生產要素的投人量。在短期內,廠商只有一部分生產要素可以變動,另一部分生產要素不能變動。例如,在短期內廠商可以改變勞動力的使用量,改變原材料、燃料等的投人量,但不能變動廠房規模和設備數量。於是成本也就相應的分成可變成本和固定成本。而在長期內,廠商的全部生產要素投人量都可以變動,如廠房規模、機器設備數量。由此,成本相應地分為短期成本和長期成本。從長期來看,廠商量有充足的時間調整所有投人要素,不存在固定成本和可變成本的區別;但是生產者只要進行了投資,進行了調整和選擇,機器、設備、廠房等成了固定生產要素,便開始了短期的經營。因此長期成本是計劃中的成本,經營中的成本是短期成本,長期成本與短期成本的這種辯證關係是包絡曲線形成的基礎條件。
在成本分析中,成本可以分為總成本、平均成本和邊際成本,相應的短期成本有短期總成本(STC),短期平均成本(SAC)和短期邊際成本(SMC),長期成本也有長期總成本(LTC)、長期平均成本(LAC)和長期邊際成本(LMC)之分。包絡曲線的理論只涉及到了總成本和平均成本,沒有涉及到邊際成本。對於理論的研究,無論是短期成本、長期成本,還是總成本、平均成本,所特指的對象應該是同一個行業的同一個廠商,這些成本只能是從不同的維度來描述同一個對象,因而它們在描述這一對象時,既應該有各自的特點,而且彼此之間又應該有相互關係的一致性,不應該前後矛盾。在推導包絡曲線時,“可無限細分”是一個值得註意的條件。可無限細分是相對於不可細分的條件來講的,不可細分指的是生產要素的投人只能以自然數的數量增減,例如勞動力的使用,廠商可以增加1個、2個、甚至是成百上千的勞動力,但是卻不能增加1.2個勞動力,勞動力是不可細分的生產要素。可無限細分就是可以出現1.2的情況,還可以更細,細到任意兩個數之間都可以再細分下去,這個條件實質上講的是生產規模變化的“連續性”,即發生了最微小變化的新的生產規模也是有意義的。這種“可無限細分”是一種理想狀態下的條件,只是一種理論上的抽象,它在一定程度上決定了包絡曲線的形狀。
包絡曲線的推導過程[1]
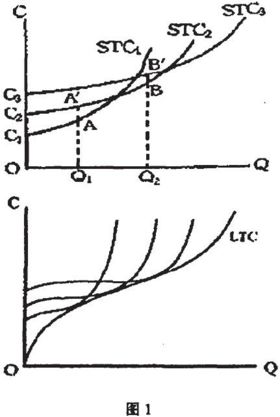
在長期成本的分析中需要指出的是,所有的生產要素都可以改變,對於某一特定的產量水平,廠商可以任意調整生產要素的投人量並實現在此基礎上的特定的生產規模,那麼廠商總會找到一個最佳的生產規模—即使用成本最低的生產規模進行生產—這個生產規模就是在長期分析中所要尋求的生產規模。沿著這一思路,並根據長期與短期的辯證關係,長期總成本曲線就可以描述了,見圖1:
在圖1中,假定STC1,STC2,STC3分別代表三條不同的短期總成本曲線,也表示三種可供選擇的生產規模。當產量為Q1時,則Q1A1 < Q1A2,廠商選擇STC1代表的生產規模;當產量為Q2時,廠商選擇STC2代表的生產規模。由此可知,廠商的長期總成本曲線是各短期總成本曲線相交點之下的弧線段相連構成的一條不規則的曲線(圖中粗線所代表的曲線)。這是生產要素不可細分條件下的長期總成本曲線的推導。如果生產要素可無限細分,包絡曲線的推導過程是完全一樣的,長期總成本曲線形狀與走勢沒有變化,只是上述的弧線段被換成了“點”——即特定產量下所需總成本的最低點,相應的包絡曲線也就變成了一條由一系列最低點連接而成的光滑的曲線(如圖lb中的LTC曲線)。從圖上看,LTC曲線是由特定產量水平下相應STC曲線上的最低點的連線構成的,即LTC曲線與所有STC曲線的最低點相切。由推導可見,長期總成本曲線是對所有相應短期總成本曲線的“包絡”,這條長期總成本曲線就被稱為對應的短期總成本曲線的包絡曲線。
包絡曲線不僅指長期總成本曲線對短期總成本曲線的包絡,而且還包括長期平均成本曲線對短期平均成本曲線的包絡。長期平均成本的地位在成本分析中尤為重要。長期平均成本可以由長期總成本與產量之商獲得,由於長期總成本曲線上的每一點都代表一個最佳生產規模即這點對應的是特定產量下的短期成本的最低點,所以長期平均成本也就表示:在長期分析中廠商生產各種產量所需要的最低平均成本。根據這一點,長期平均成本曲線也可以描繪了。
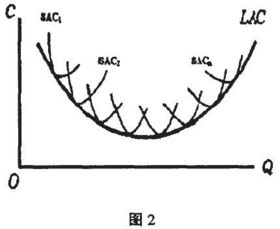
假定生產規模可以無限細分,每一個Q對應有一條SAC曲線,每條SAC曲線都有一個最低平均成本點,這些最低點就是長期分析中各產量水平所對應的最低平均成本,把這些點連起來就是長期平均成本曲線,見圖2。同樣,長期平均成本曲線也是與所有短期平均成本曲線的最低點相切的曲線。
到此,長期成本曲線對相應短期成本曲線的兩條包絡曲線已經得到了——所有短期總成本曲線的最低點與對應長期總成本曲線相切,即所有的短期平均成本曲線的最低點與長期平均成本曲線相切——所以筆者將包絡曲線定義為,包絡曲線是由所有短期成本曲線(總成本曲線和平均成本曲線)最低點軌跡構成的相應的長期成本曲線。
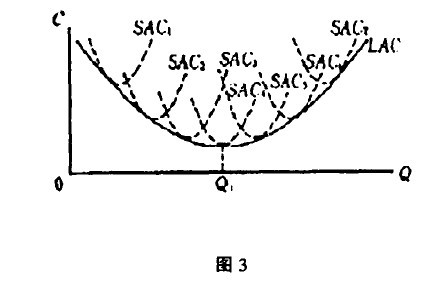
筆者參考了幾個版本的西方經濟學教材,關於包絡曲線的推導到這裡並無異議。特定產量的短期總成本的最低點與相應的短期平均成本的最低 點,兩者是相呼應的,見圖3。兩者從不同的角反映了某個廠商的長期成本計劃,這體現了包絡曲線在長期總成本與長期平均成本之間是一致的。而筆者把兩條包絡曲線的推導在此演示出,目的就在於說明推導的前後一致性。








只有在長期平均成本最低點時才與短期成本最低點相切吧?