數學模型
出自 MBA智库百科(https://wiki.mbalib.com/)
數學模型(Mathematical Model)
目錄 |
數學模型是針對參照某種事物系統的特征或數量依存關係,採用數學語言,概括地或近似地表述出的一種數學結構,這種數學結構是藉助於數學符號刻畫出來的某種系統的純關係結構。從廣義理解,數學模型包括數學中的各種概念,各種公式和各種理論。因為它們都是由現實世界的原型抽象出來的,從這意義上講,整個數學也可以說是一門關於數學模型的科學。從狹義理解,數學模型只指那些反映了特定問題或特定的具體事物系統的數學關係結構,這個意義上也可理解為聯繫一個系統中各變數間內的關係的數學表達。
數學模型所表達的內容可以是定量的,也可以是定性的,但必須以定量的方式體現出來。因此,數學模型法的操作方式偏向於定量形式。
建立數學模型的要求:
1、真實完整。
1)真實的、系統的、完整的反映客觀現象;
2)必須具有代表性;
3)具有外推性,即能得到原型客體的信息,在模型的研究實驗時,能得到關於原型客體的原因;
4)必須反映完成基本任務所達到的各種業績,而且要與實際情況相符合。
2、簡明實用。在建模過程中,要把本質的東西及其關係反映進去,把非本質的、對反映客觀真實程度影響不大的東西去掉,使模型在保證一定精確度的條件下,儘可能的簡單和可操作,數據易於採集。
3、適應變化。隨著有關條件的變化和人們認識的發展,通過相關變數及參數的調整,能很好的適應新情況。
1、 精確型:內涵和外延非常分明,可以用精確數學表達。
2、 模糊型:內涵和外延不是很清晰,要用模糊數學來描述。
1、簡化原則
現實世界的原型都是具有多因素、多變數、多層次的比較複雜的系統,對原型進行一定的簡化即抓住主要矛盾,數學模型應比原型簡化,數學模型自身也應是“最簡單”的。
2、可推導原則
由數學模型的研究可以推導出一些確定的結果,如果建立的數學模型在數學上是不可推導的,得不到確定的可以應用於原型的結果,這個數學模型就是無意義的。
3、反映性原則
數學模型實際上是人對現實世界的一種反映形式,因此數學模型和現實世界的原型就應有一定的“相似性”,抓住與原型相似的數學表達式或數學理論就是建立數學模型的關鍵性技巧。
1、解決對客觀現象進行試驗的困難。
2、比較容易操作。
3、模型試驗能夠比較節約。
4、可以揭示客觀對象本質。
1、提出問題並用準確的語言加以表述。
2、分析各種因素,作出理論假設。
3、建立數學模型。
4、按數學模型進行數學推導,得出有意義的數學結果。
5、對數學結論進行分析。若符合要求,可以將數學模型進行一般化和體系化按此解決問題若不符合,則進一步探討,修改假設,重建模型,直止符合要求為止。
6、優化。對一個問題的假設和數學模型不斷加以修改,進行最優化處理。因為對一個問題或一類問題也可能有幾個模型,以對它們要進行比較,直到找到最優模型。
數學模型案例分析[1]
- 1.轉庫流向優化及時間推薦
轉庫流向優化及時間推薦和業務需求的提出轉庫決策主要是從末端庫漲庫的角度考慮轉庫問題,是完成推薦轉庫準發的功能。一個準發是否最終實現轉庫,取決於末端庫、成品庫、準發數量、品種的情況和限制。準發因其品種的不同可以轉向的成品庫有差異,從具體成品庫的角度看,在能力不能滿足所有準發轉庫需求的情況下,必須在準發集合中作出取捨;類似的情形也適用於末端庫。這就是轉庫流向優化及時間推薦模型建立的原因。首先,用戶希望盡多準發轉向最合適的目的庫,也就是儘可能的轉庫。其次,對於某些準發(具體就是合同總重量大於1000噸並上一條船的準發),希望其儘可能的均勻轉庫。比如有一個2000噸的合同(其中包括10個準發),此合同可以轉向5個成品庫,那麼目標就是轉向每個成品庫的準發總重都是400噸。一般情況下,由於準發是不可拆分的,此目標不能嚴格達到,那麼就希望總重儘量接近400噸。受客觀因素的限制,準發轉庫的完成要受三類約束條件的限制,第一類是要滿足末端庫出庫能力的約束;第二類是成品庫庫容的約束;第三類是成品庫入庫能力的約束。由於末端庫和成品庫均不是一個,每類實際上都是多個約束。
- 2.轉庫原則
對於每個待轉庫的準發,它可轉向的庫之間有一個優先順序,此順序確定的原則如下:。
末端庫向成品庫轉,末端庫間不轉;。
優先轉向廠內成品庫。
鐵路庫的存放原則如下:
A.跨放鋼管;
B.跨優先放鋼管,可放管坯,大方坯,方坯;
C.跨主要放鋼捲,也可以放鋼坯,鋼板;
D.跨主要放鋼板,也可以放板坯、方坯、鋼捲;
E,F跨放冷熱板捲(主要存放出口產品);
A,B跨可以混用,但不能於其它跨混用;
C,D,E,F跨可以混用。
運輸方式已定情況:
廠內鐵運全放鐵路庫;鋼坯優先放鐵路庫,可放堆放場,鋼壞堆場;
水運:冷軋產品優先放碼頭庫,可放鐵路庫;熱軋產品國外優先鐵路庫,其次放碼頭庫,也可放堆場,國內堆場優先;。
鋼坯全放堆場;鋼管放鐵路庫;
當多個準發進行轉庫競爭時,必須需要確定准發的優先順序別。具體原則如下:
(1)分品種轉庫原則:冷軋產品:優先往碼頭庫轉,其次往鐵路庫轉,不能露天存放;熱軋產品:出口熱軋捲、鋼坯優先放堆場,然後考慮往鐵路庫轉,熱軋板(出口、國內)放鐵路庫D跨,國內熱軋捲,對於水運產品,放碼頭庫;對於鐵運產品,放鐵路庫C跨,其次放堆場,鋼壞原則上放堆場,鋼管全放鐵路庫。
(2)汽運、漲庫的轉庫原則同水運。
(3)優先順序的確定原則:優先考慮當日15點至次日15點的車船合同,優先順序為直裝、漲庫、其它:準發單不能拆,優先考慮大的準發單;在製品轉庫按成品對待,優先順序按(3)中的“其它”項對待;
- 3.數學模型描述
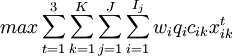 (1)
(1)
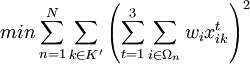 (2)
(2)
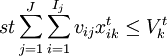 ,t = 1,2,3;
,t = 1,2,3;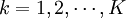 (3)
(3)
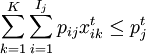 ,t = 1,2,3;
,t = 1,2,3;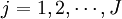 (4)
(4)
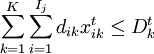 ,t = 1,2,3;
,t = 1,2,3;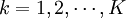 (5)
(5)
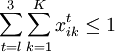 ,
,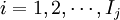 ;
;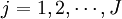 (6)
(6)
各參數的意義如下:
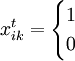
| 第i個準發在第t班轉向k庫 |
其他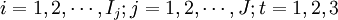
|
j:需轉庫準發所涉及的末端庫,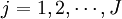 ;
;
Ij:j庫需轉庫的準發集合,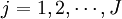 ;
;
k:轉庫所涉及的成品庫,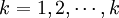 ;
;
cik:i準發轉至k庫之“收益”;
wi:i準發的重量(噸);
qi:i準發的權重繫數;
n:總數量大於等於103噸並同上一條船的合同(或屬同一齣品聯絡單)數量,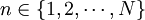 ;
;
K':總數量大於等於103噸並同上一條船的合同(或屬同一齣口聯絡單)可能轉向的成品庫集合;
Ωn:第n個總數量大於等於103噸並同上一條船的合同(或屬同一齣口聯絡單)包含的準發的個數;
vik:i準發轉向k庫時占用的k庫庫容;
Vtk:k庫在第t班的剩餘庫容;
Pij:j庫i準發出庫所需能力(件數);
Pjt:j庫在第t班轉庫可用的出庫能力(件數);
dik:i準發轉至k庫所需的入庫能力(件數);
Dtk:k庫在第t班轉庫可用的入庫能力(單位為件數)。
- 4.解法思想簡介及結果
從上面的模型描述中可以看出,這個問題是一個線性整數規劃問題,(且為二次0-1規劃,同時也是多目標模型)。從解決問題的角度看,當準發數目少時,問題為小規模0-1規劃問題,使用線性規劃(LP)模塊可以解決,而當準發多時問題為大規模0—1規劃問題,運行LP模塊的花費時間已不能滿足實際問題的要求,因為其複雜性已屬於指數增長的問題。所以調用現成的程式在其時效上已經是不可行的,這類問題被稱NP—完全問題。
在本問題中主要採用兩種演算法:一種為啟髮式演算法(貪婪演算法),另一種為混合演算法(線性規劃和啟髮式相結合的演算法)。
這個模型有兩個目標,目標一的對象是合同重小於一千噸的準發,而目標二的對象為合同重大於等於一千噸的準發,兩種準發共用倉庫的能力。多目標問題是一類難於求解的問題,解決這一類問題的方法主要有目標加權法、目標規劃等。考慮到流向優化及時間推薦模型的一些特殊性,本項目採用的是簡單但是合理的一種解法。實際問題是合同重於一千噸的準發數量少,合同不重於一千噸的準發是大量的,分散轉庫的要求不但重要而且易於滿足。因此工程中採用的是兩種準發分別處理的方法,即首先處理重於一千噸的準發,能力允許時再轉不重於一千噸的準發,這相當於目標加權法中給第一個目標很大的權值。
這種方法不能推廣到更一般問題,使用這種方法完全是由於問題的特殊性決定。這樣處理後,兩個目標可以分開處理,歸入第一個目標的準發數量小,使用啟髮式演算法求解;屬於第二個目標的準發數量巨大,使用線性規劃加啟髮式演算法的方法求解。
單獨考慮目標一的問題在數學上可概括為二次0-1規劃,它是N個式子每兩個之差的平方和最小,要求它們之間的差距最小,故可稱為平衡問題。
當變數為實數時,這N個式子的值全相等時目標值最小,但對於0-1變數則一般不會出現這種情況。
從約束來看,這些約束都是小於等於約束,因此是一個典型的資源約束問題。有N個庫(成品庫)要接受一批准發,在滿足三種能力的條件下,希望轉到每個庫中的準發總重一樣大,而且這些準發都是儘量要轉庫的(轉比不轉好)。根據以上問題的特點,可以把追求每個式子都等於一個定值作為目標。因此把準發總重用N平均,並把這個值(以後稱做期望值)作為每個庫希望接受準發總重的目標,這和原問題是等價的。因此,就可以對於每個庫分別確定轉向它的準發集合,使此準發集合的總重儘量接近期望值,這樣當所有的目標庫轉向的準發均確定後,總的結果就是每個庫轉向的準發總重是一樣的。剩下的問題就是對於一個具體的目標庫(成品庫)和一個期望轉入的準發總重,如何找出轉向它的準發集合。本文使用的方法就是上面說的啟髮式演算法,具體的演算法由兩個演算法框圖SglRdy和AtMost給出(略)。其中SglRdy的作用就是從可選準發集合中選擇重量大於等於期望值的準發進行轉庫(因為一旦有這樣的準發存在,只轉一個準發就夠了),如果有的話就返回,否則調用AtMost。AtMost的作用就是力求選取總重小於等於期望值的準發集合,使它們的總重儘量接近期望值。這是一種不回溯的搜索演算法。
- ↑ 高天 王志福 劉曉剛.大型企業庫存管理中的數學模型——轉庫流向優化及時間推薦.錦州師範學院學報(自然科學版).2000年02期








相當有深度!!