價格數學模型

用手机看条目

出自 MBA智库百科(https://wiki.mbalib.com/)

價格數學模型(Mathematical Model Of Price)

什麼是價格數學模型^[1]

　　價格數學模型運用數學方法對價格形成和價格變動規律所作的描述。經濟學所運用的數學模型可以分為兩類：一類是用於揭示經濟客體本質規律但不能用於具體技術的，如C+V+M；另一類是可以用於計算的。通常所說的經濟數學模型，多指後一類。

價格數學模型的分類

　　依方法論不同，可用於計算的價格數學模型大致分為兩類：一類是從價格形成的內在機制上來描述經濟變數中的數量關係；另一類是從經濟事物的錶面現象上探索經濟變數間的內在聯繫。還有一類模型是把這兩類模型組合起來，形成一個組合模型。應用的數學領域，涉及線性代數、數學規劃、數理統計等數學分支。現在這類研究還在深入發展，涉及的數學領域也越來越廣泛。最常見的價格數學模型是投入產出價格模型。

[編輯]

市場價格數學模型的確立與分析^[2]

　　對於純粹的市場經濟來說，商品市場價格取決於市場供需之間的關係，市場價格能促使商品的供給與需求相等(這樣的價格稱為(靜態)均衡價格)。也就是說，如果不考慮商品價格形成的動態過程，那麼商品的市場價格應能保證市場的供需平衡，但是，實際的市場價格+會恰好等於均衡價格，而且價格也不會是靜態的，應是隨時間不斷變化的動態過程。

　　例試建立描述市場價格形成的動態過程的數學模型。

　　解假設在某一時刻，商品的價格為p(t)，它與該商品的均衡價格間有差別，此時，存在供需差，此供需差促使價格變動。對新的價格，又有新的供需末，如此不斷調節，就構成市場價格形成的動態過程，假設價格p(t)的變化率dp/dt與需求和供給之差成正比，並記f(p，r)為市求函數，g(p)為供給函數(為r參數)，於是:

　　 $\begin{cases}dp/dt=\alpha[f(p,r)-g(p)],\\p(0)=p_0,\end{cases}$

　　其中 $p 0$ 為商品在t=O時劃的價格， $α$ 為正常數。

　　若設，f(p，r)=-ap+b，g(p)=cp+d，則上式變為:

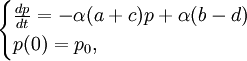　　 $\begin{cases}\frac{dp}{dt}=-\alpha(a+c)p+\alpha(b-d)\\p(0)=p_0,\end{cases}$ 　　①

　　其中a，b，c，d均為正常數，其解為：

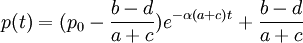
　　 $p(t)=(p_0-\frac{b-d}{a+c})e^{-\alpha(a+c)t}+\frac{b-d}{a+c}$

　　下麵對所得結果進行討論:

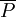　　 $\overline{P}$ 設為靜態均衡價格，則其應滿足:

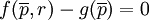
　　 $f(\overline{p},r)-g(\overline{p})=0$

　　即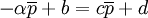 $-\alpha\overline{p}+b=c\overline{p}+d$ ,

　　於是得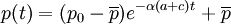： $p(t)=(p_0-\overline{p})e^{-\alpha(a+c)t}+\overline{p}$ ，從而價格函數p(t)可寫為：。

　　 $p(t)=(P_0-\overline{p})e^{-\alpha(a+c)t}+\overline{p}$ ,

　　令→+∞，取極限得：

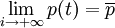
　　 $\lim_{i \to +\infty}p(t)=\overline{p}$

　　這說明，市場價格逐步趨於均衡價格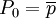 $P_0=\overline{p}$ 。又若初始價格，則動態價格就維持在均衡價格\overline(p)上，整個動態過程就化為靜態過程；

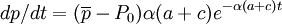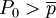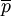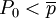　　(2)由於 $dp/dt=(\overline{p}-P_0)\alpha(a+c)e^{-\alpha(a+c)t}$ ，所以，當 $P_0>\overline{p}$ 時，dp/dt<0，p(t),單調下降向靠 $\overline{p}$ 攏；當 $P_0<\overline{p}$ 時，當dp/dt>0，p(t),單調增加向 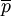$\overline{p}$ 靠攏。