多元線性回歸分析預測法
出自 MBA智库百科(https://wiki.mbalib.com/)
多元線性回歸分析預測法(Multi factor line regression method,多元線性回歸分析法)
目錄 |
在市場的經濟活動中,經常會遇到某一市場現象的發展和變化取決於幾個影響因素的情況,也就是一個因變數和幾個自變數有依存關係的情況。而且有時幾個影響因素主次難以區分,或者有的因素雖屬次要,但也不能略去其作用。例如,某一商品的銷售量既與人口的增長變化有關,也與商品價格變化有關。這時採用一元回歸分析預測法進行預測是難以奏效的,需要採用多元回歸分析預測法。
多元回歸分析預測法,是指通過對兩個或兩個以上的自變數與一個因變數的相關分析,建立預測模型進行預測的方法。當自變數與因變數之間存線上性關係時,稱為多元線性回歸分析。
多元線性回歸的計算模型[1]
一元線性回歸是一個主要影響因素作為自變數來解釋因變數的變化,在現實問題研究中,因變數的變化往往受幾個重要因素的影響,此時就需要用兩個或兩個以上的影響因素作為自變數來解釋因變數的變化,這就是多元回歸亦稱多重回歸。當多個自變數與因變數之間是線性關係時,所進行的回歸分析就是多元線性回歸。
設y為因變數,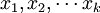 為自變數,並且自變數與因變數之間為線性關係時,則多元線性回歸模型為:
為自變數,並且自變數與因變數之間為線性關係時,則多元線性回歸模型為:
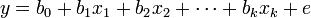
其中,b0為常數項,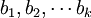 為回歸繫數,b1為
為回歸繫數,b1為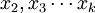 固定時,x1每增加一個單位對y的效應,即x1對y的偏回歸繫數;同理b2為x1,xk固定時,x2每增加一個單位對y的效應,即,x2對y的偏回歸繫數,等等。如果兩個自變數x1,x2同一個因變數y呈線性相關時,可用二元線性回歸模型描述為:
固定時,x1每增加一個單位對y的效應,即x1對y的偏回歸繫數;同理b2為x1,xk固定時,x2每增加一個單位對y的效應,即,x2對y的偏回歸繫數,等等。如果兩個自變數x1,x2同一個因變數y呈線性相關時,可用二元線性回歸模型描述為:
y = b0 + b1x1 + b2x2 + e
建立多元性回歸模型時,為了保證回歸模型具有優良的解釋能力和預測效果,應首先註意自變數的選擇,其準則是:
(1)自變數對因變數必須有顯著的影響,並呈密切的線性相關;
(2)自變數與因變數之間的線性相關必須是真實的,而不是形式上的;
(3)自變數之間具有一定的互斥性,即自變數之間的相關程度不應高於自變數與因變數之間的相關程度;
(4)自變數應具有完整的統計數據,其預測值容易確定。
多元性回歸模型的參數估計,同一元線性回歸方程一樣,也是在要求誤差平方和(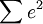 )為最小的前提下,用最小二乘法求解參數。以二線性回歸模型為例,求解回歸參數的標準方程組為:
)為最小的前提下,用最小二乘法求解參數。以二線性回歸模型為例,求解回歸參數的標準方程組為:

解此方程可求得b0,b1,b2的數值。亦可用下列矩陣法求得
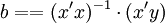
即

多元線性回歸模型的檢驗[1]
多元性回歸模型與一元線性回歸模型一樣,在得到參數的最小二乘法的估計值之後,也需要進行必要的檢驗與評價,以決定模型是否可以應用。
1、擬合程度的測定。
與一元線性回歸中可決繫數r2相對應,多元線性回歸中也有多重可決繫數r2,它是在因變數的總變化中,由回歸方程解釋的變動(回歸平方和)所占的比重,R2越大,回歸方各對樣本數據點擬合的程度越強,所有自變數與因變數的關係越密切。計算公式為:
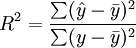
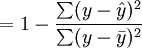
其中,
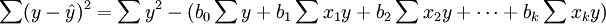
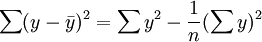
2.估計標準誤差
估計標準誤差,即因變數y的實際值與回歸方程求出的估計值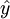 之間的標準誤差,估計標準誤差越小,回歸方程擬合程度越強。
之間的標準誤差,估計標準誤差越小,回歸方程擬合程度越強。
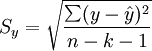

其中,k為多元線性回歸方程中的自變數的個數。
3.回歸方程的顯著性檢驗
回歸方程的顯著性檢驗,即檢驗整個回歸方程的顯著性,或者說評價所有自變數與因變數的線性關係是否密切。常採用F檢驗,F統計量的計算公式為:
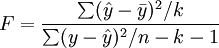
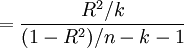
根據給定的顯著水平a,自由度(k,n-k-1)查F分佈表,得到相應的臨界值Fa,若F > Fa,則回歸方程具有顯著意義,回歸效果顯著;F < Fa,則回歸方程無顯著意義,回歸效果不顯著。
4.回歸繫數的顯著性檢驗
在一元線性回歸中,回歸繫數顯著性檢驗(t檢驗)與回歸方程的顯著性檢驗(F檢驗)是等價的,但在多元線性回歸中,這個等價不成立。t檢驗是分別檢驗回歸模型中各個回歸繫數是否具有顯著性,以便使模型中只保留那些對因變數有顯著影響的因素。檢驗時先計算統計量ti;然後根據給定的顯著水平a,自由度n-k-1查t分佈表,得臨界值ta或ta / 2,t > t − a或ta / 2,則回歸繫數bi與0有顯著差異,反之,則與0無顯著差異。統計量t的計算公式為:
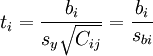
其中,Cij是多元線性回歸方程中求解回歸繫數矩陣的逆矩陣(x'x) − 1的主對角線上的第j個元素。對二元線性回歸而言,可用下列公式計算:
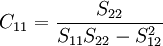
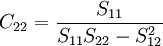
其中,
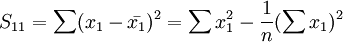
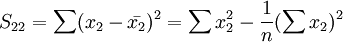
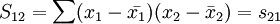
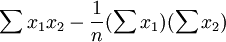
5.多重共線性判別
若某個回歸繫數的t檢驗通不過,可能是這個繫數相對應的自變數對因變數的影響不顯著所致,此時,應從回歸模型中剔除這個自變數,重新建立更為簡單的回歸模型或更換自變數。也可能是自變數之間有共線性所致,此時應設法降低共線性的影響。
多重共線性是指在多元線性回歸方程中,自變數之間有較強的線性關係,這種關係若超過了因變數與自變數的線性關係,則回歸模型的穩定性受到破壞,回歸繫數估計不准確。需要指出的是,在多元回歸模型中,多重共線性的難以避免的,只要多重共線性不太嚴重就行了。
判別多元線性回歸方程是否存在嚴重的多重共線性,可分別計算每兩個自變數之間的可決繫數r2,若r2 > R2或接近於R2,則應設法降低多重線性的影響。亦可計算自變數間的相關係數矩陣的特征值的條件數k = λ1 / λp(λ1為最大特征值,λp為最小特征值),k<100,則不存在多重點共線性;若100≤k≤1000,則自變數間存在較強的多重共線性,若k>1000,則自變數間存在嚴重的多重共線性。降低多重共線性的辦法主要是轉換自變數的取值,如變絕對數為相對數或平均數,或者更換其他的自變數。
6.D.W檢驗
當回歸模型是根據動態數據建立的,則誤差項,若誤差序列諸項之間相互獨立,則誤差序列各項之間沒有相關關係,若誤差序列之間存在密切的相關關係,則建立的回歸模型就不能表述自變數與因變數之間的真實變動關係。D.W檢驗就是誤差序列的自相關檢驗。檢驗的方法與一元線性回歸相同。
案例一:公路客貨運輸量多元線性回歸預測方法探討[2]
一、背景
公路客、貨運輸量的定量預測,有助於促進了公路運輸經營決策的科學化和現代化。
線性回歸分析法是以相關性原理為基礎的,相關性原理是預測學中的基本原理之一。由於公路客、貨運輸量受社會經濟有關因素的綜合影響。所以,多元線性回歸預測首先是建立公路客、貨運輸量與其有關影響因素之間線性關係的數學模型。然後通過對各影響因素未來值的預測推算出公路客貨運輸量的預測值。
二、公路客、貨運輸量多元線性回歸預測方法的實施步驟
1.影響因素的確定
影響公路客貨運輸量的因素很多,主要包括以下一些因素:
(1)客運量影響因素
人口增長量、國民生產總值、國民收入工農業總產值,基本建設投資額城鄉居民儲蓄額鐵路和水運客運量等。
(2)貨運量影響因素
人口貨車保有量(包括拖拉機),國民生產總值,國民收入、工農業總產值,基本建設投資額,主要工農業產品產量、社會商品購買力、社會商品零售總額、鐵路和水運貨運量額。
上述影響因素僅是對一般而言,在針對具體研究對象時會有所增減。因此,在建立模型時只須列入重要的影響因素,對於非重要因素可不列入模型中。若疏漏了某些重要的影響因素,則會造成預測結果的失真。另外,影響因素太少會造成模型的敏感性太強。反之,若將非重要影響因素列入模型,則會增加計算工作量,使模型的建立複雜化並增大隨機誤差。
影響因素的選擇是建立預測模型首要的關鍵環節,可採取定性和定量相結合的方法進行,影響因素的確定可以通過專家調查法,其目的是為了充分發揮專家的聰明才智和經驗。
具體做法就是通過對長期從事該地區公路運輸企業和運輸管理部門的領導幹部、專家、工作人員和行家進行調查。可通過組織召開座談會,也可以通過採訪,填寫調查表等方法進行,從中選出主要影響因素為了避免影響因素確定的隨意性,提高回歸模型的精度和減少預測工作量,可通過查閱有關統計資料後,再對各影響因素進行相關度(或關聯度)和共線性分析,從而再次篩選出最主要的影響因素,所謂相關度分析就是將各影響因素的時間序列與公路客貨運量的時間序列做相關分析事先確定—個相關係數,對相關係數小的影響因素進行淘汰,關聯度是灰色系統理論中反映事物發展變化過程中各因素之間的關聯程度,可通過建空公路客、貨運量與各影響影響因素之間關聯繫數矩陣,按一定的標準繫數捨去關聯度小的影響因素,所謂共線性是指某些影響因素之間存在著線性關係或接近於線性關係,由於公路運輸經濟自身的特點,影響公路客,貨運輸量的諸多因素之間總是存在著一定的相關性,持別是與國民經濟有關的一些價值型指標。
我們研究的不是有無相關性問題而是共線性的程度,如果影響因素之間的共線性程度很高,首先會降低參數估計值的精度。其次在回歸方程建立後的統計檢驗中導致捨去重要的影響因素或錯誤地接受無顯著影響的因素,從而使整個預測工作失去實際意義。關於共線性程度的判定,可利用逐步分析估計法的數理統計理論編製電腦程式來實現。或者通過比較rij和R2的大小來判定。在預測學上,一般認為當rij > R2時,共線性是嚴重的,其含義是,多元線性回歸方程中所含的任意兩個自變數xi,xj之間的相關係數rij大於或等於該方程的樣本可決繫數R2時,說明自變數中存在著嚴重的共線性問題。
2.建立經驗線性回歸方程
利用最小二乘法原理尋求使誤差平方和達到最小的經驗線性回歸方程:
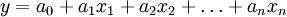
y——預測的客、貨運量
g——各主要影響因數
3.數據整理
對收集的歷年客、貨運輸量和各主要影響因素的統計資料進行審核和加工整理是為了保證預測工作的質量。
資料整理主要包括下列內容:
(1)資料的補缺和推算。
(2)對不可靠資料加以核實調整,對查明原因的異常值加以修正。
(3)對時間序列中不可比的資料加以調整和規範化;對按當年價格計算的價值指標應折算成按統。
4.多元線性回歸模型的參數估計
在經驗線性回歸模型中,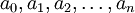 是要估計的參數,可通過數理統計理論建立模型來確定。在實際預測中,可利用多元線性回歸相關分析的電腦程式來實現。
是要估計的參數,可通過數理統計理論建立模型來確定。在實際預測中,可利用多元線性回歸相關分析的電腦程式來實現。
5.對模型參數的估計值進行檢驗。
此項工作的目的在於判定估計值是否滿意、可靠。一般檢驗工作須從以下幾方面來進行。
- 經濟意義檢驗
關於經濟預測的數學模型,首先要檢驗模型是否有經濟意義,γp若參數估計值的符號和大小與公路運輸經濟發展以及經濟判別不符合時,這時所估計的模型就不能或很難解釋公路運輸經濟的一般發展規律,就應拋棄這個模型,需要重新構造模型或重新挑選影響因素。
- 統計檢驗
統計檢驗是數理統計理論的重要內容,用於檢驗模型估計值的可靠性。通常,在公路客、貨運量預測中應採用的統計檢驗是:
- 擬合度檢驗
所謂擬合度是指所建立的模型與觀察的實際情況軌跡是否吻合、接近,接近到什麼程度。統計學是通過構造統計量R2來度量的,R2可由樣本數據計算得出。若建立的模型愈接近於實際,則R^2愈接近於1。
- 回歸方程的顯著性檢驗
回歸方程的顯著性檢驗是通過方差分析構造統計量F來進行的,統計量F是通過樣本數據計算得出的。當給定某一置信度後,可以通過查閱F表來確定回歸模型從總體效果來看是否可以採納。
- 參數估計值的標準差檢驗
估計值的標準差是衡量估計值與真實參數值的離差的一種量度。參數的標準差越大,估計值的可靠性也就越小;反之,如果標準差越小,那麼估計值的可靠性也就越大。參數值標準差的檢驗,可以通過構造大統計量來進行量度。當給定某一置信度後,可以通過查表來確定模型中某個參數估計值的可靠性。
應當強調指出,統計檢驗相對於經濟意義檢驗來說是第二位的。如果經濟意義檢驗不合理,那麼即使統計檢驗可以達到很高的置信度,也應當拋棄這種估計結果,因為用這樣的結果來進行經濟預測是沒有意義的。
6.最優回歸方程的確定
經過上述的經濟意義和統計檢驗後,挑選出的線性回歸方程往往是好幾個、為了從中優選出用於進行實際預測的方程,我們可以採用定性和定量相結合的辦法。
從數理統計的原理來講,應挑選方程的剩餘均方較小為好,但作為經濟預刪還必須儘量考慮到方程中的影響因素更切合實際和其未來值更易把握的原則來綜合考慮。當然、有時也可以從中挑選出好幾個較優的回歸方程,通過預測後,分別作為不同的高、中、低方案以供決策人員選擇。
7.模型的實際預測檢驗
在獲得模型參數估計值後,又經過了上述一系列檢驗而選出的最優(或較優)回歸方程,還必須對模型的預測能力加以檢驗。不難理解、最優回歸方程對於樣本期間來說是正確的,但是對用於實際預測是否合適呢?為此,還必須研究參數估計值的穩定性及相對於樣本容量變化時的靈敏度,也必須研究確定估計出來的模型是否可以用於樣本觀察值以外的範國,其具休做法是:
(1)採用把增大樣本容量以後模型估計的結果與原來的估計結果進行比較,並檢驗其差異的顯著性。
(2)把估計出來的模型用於樣本以外某一時間的實際預測,並將這個預測值與實際的觀察值作一比較,然後檢驗其差異的顯著性。
8.模型的應用
公路客、貨運輸量多元線性回歸預測模型的研究目的主要有以下幾個方面。
(1)進行結構分析,研究影響該地區的公路客、貨運輸量的主要因素和各影響因素影響程度的大小,進一步探討該地區公路運輸經濟理論。
(2)預測該地區今後年份的公路客、貨運輸量的變化,以便為公路運輸市場、公路運輸政策及公路運輔建設項目投資作出正確決策提供理論依據。另外,還可以通過公路客、貨運輸量與公路交通量作相關分析來對公路的飽和度發展趨勢進行預測。從而為公路的新建、擴建項目的投資提供決策分析。
(3)模擬各種經濟政策下的經濟效果,以便對有關政策進行評價。
四、經調查分析,影響某地區旅客運輸量的因素為:
x1——國民收入
x2——工農業總產值
x3——社會總產值
x4——人口
x5——客車保有量
x6——城鄉居民儲蓄存款
經計算得下列相關係數表:
| x1 | x2 | x3 | x4 | x5 | x6 | |
| Y | 0.9439 | 0.9287 | 0.9043 | 0.9914 | 0.9670 | 0.7021 |
| Z | 0.9736 | 0.96l4 | 0.9326 | 0.8645 | 0.9321 | 0.6678 |
Y——客運盈
Z——旅客周轉量
若令α = 0.85,則可以捨去x6這個影響因素,也就是認為“城鄉居民儲蓄存款”不能作為響旅客運輸量的主要因素。
2.經調查分析、影響某地區旅客運輸量的因素為:
x1——國民收入
x2——工農業總產值
x3——社會總產值
x4——人口
x5——客車保有量
x6——國民生產總值
x7——公路通車裡程
經計算得客運量和旅客周轉量的經驗線性回歸方程如下:
Y = α0 + α1x1 + α2x2 + α5x5 R2 = 0.9997
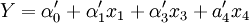 R2 = 0.9962
R2 = 0.9962
Z = β0 + β4x4 + β5x5 + β7x7 R2 = 0.9983
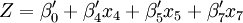 R2 = 0.9990
R2 = 0.9990
Y——客運盈
Z——旅客周轉量
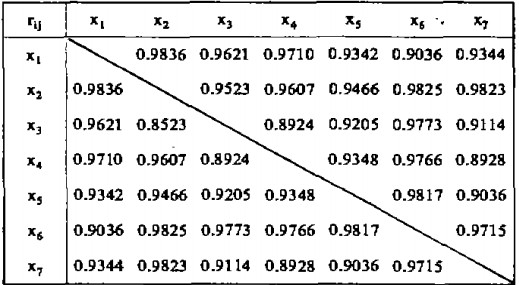
各自變數間的相關係數表如下:
由上述計算可知,四個方程中均未出現rij > R2的情況,因此可以認為各自方程中的影響因素之間不存在嚴重共線性問題。
3.經調查分析,影響某地區貨運周轉量的因素為:
x1——國民收入
x2——工農業總產值
x3——基建投資額
x4——原煤產量
x5——鋼鐵、化肥、水泥、糧食總產量
x6——國民總產值
x7——社會商品零售總額
x8——相鄰地、市工農業總產值的平均值
Y = a0 + a4x4 + a6x6 + a7x7 (1)
其中:R2=0.9875 F=206.33 S·E=1673.24
t4=-2.8321 t6=3.1407 t7=2.7431
Y = b0 + b2x2 + b4x4 (2)
其中:R2=0.9764 F=164.59 S·E=1044.27
- ↑ 1.0 1.1 龔曙明.市場調查與預測/清華大學出版社, 2005 .ISBN 7810824708, 9787810824705
- ↑ 馬進.公路客貨運輸量多元線性回歸預測方法探討[J].汽車運輸研究.1994(1)
本条目由以下用户参与贡献
Angle Roh,funwmy,Zfj3000,Vulture,Xiangtaiyan,Cabbage,Fghghg,Yixi,Yongjieyan,Tears~,HEHE林,姜鹏,连晓雾,y桑,Tracy,寒曦,Jiang Ze,张雷,Mis铭,Llyn.評論(共39條)
太差了
條目內容若有不足或未完善,歡迎指正,或直接參与編輯。
關於“回歸繫數顯著性檢驗”一段落中,回歸繫數的t檢驗值的計算公式沒有列出,疑似只複製了文本而漏掉了圖片?
謝謝指正,已進行修改完善
希望以後改善:輸入“F檢驗”根本跳不到這個頁面,搜索功能太差,很難找到自己想要的
由於F檢驗是重定向到方差分析里的,因此搜索的時候顯示的會是方差分析
b1,b2如果出現負值表明什麼含義
我也有同樣的問題,如果是負值,能否照常使用?
您可進入多元非線性回歸分析希望對您有幫助!
我有一個問題,一直也沒搞清楚,想請教你一下。在多元回歸線性回歸分析之前,是否一定要做相關性分析?如果做相關性分析,那麼它的作用或目的是什麼?勞煩高手了?
我有一個問題,一直也沒搞清楚,想請教你一下。在多元回歸線性回歸分析之前,是否一定要做相關性分析?如果做相關性分析,那麼它的作用或目的是什麼?勞煩高手了?
一定要做相關性分析,相關係數高的變數要剔除,為了保持各個變數之間的獨立性,這樣才能做多元的線性回歸。
請教:如果是2組多元數據,因數相同,進行多元回歸,得到2個多元回歸方程,常數項基本相同,如2個方程:y=10x1+90x2+100,y=20x1+50x2+105,對於這2個方程可不可以認為相對於y,第2組樣本x1因數的敏感性高於第1組樣本,x2因數的敏感性低於第1組樣本。謝謝!
自變數之彰是什麼意思,看不明白
自變數之間,錯別字,改了
解析失敗 (PNG 轉換失敗; 請檢查是否正確安裝了 latex, dvips, gs 和 convert): x_1
寫的太好了,就是很多圖片沒有








真棒