全球专业中文经管百科，由121,994位网友共同编写而成，共计435,843个条目

查看

工具▼

多元非線性回歸分析

用手机看条目

出自 MBA智库百科(https://wiki.mbalib.com/)

目錄

1 什麼是多元非線性回歸分析
2 多元非線性回歸分析方程
3 多元非線性回歸分析模型[1]
4 參考文獻

什麼是多元非線性回歸分析

　　多元非線性回歸分析是指包含兩個以上變數的非線性回歸模型。對多元非線性回歸模型求解的傳統做法，仍然是想辦法把它轉化成標準的線性形式的多元回歸模型來處理。有些非線性回歸模型，經過適當的數學變換，便能得到它的線性化的表達形式，但對另外一些非線性回歸模型，僅僅做變數變換根本無濟於事。屬於前一情況的非線性回歸模型，一般稱為內蘊的線性回歸，而後者則稱之為內蘊的非線性回歸。

多元非線性回歸分析方程

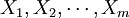　　如果自變數 $X_1,X_2,\cdots,X_m$ 與依變數Y皆具非線性關係，或者有的為非線性有的為線性，則選用多元非線性回歸方程是恰當的。例如，二元二次多項式回歸方程為：

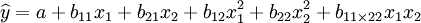
　　 $\widehat{y}=a+b_{11}x_1+b_{21}x_2+b_{12}x_1^2+b_{22}x_2^2+b_{11\times22}x_1x_2$

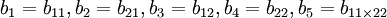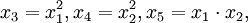　　令 $b_1=b_{11},b_2=b_{21},b_3=b_{12},b_4=b_{22},b_5=b_{11\times22}$ ,及 $x_3=x_1^2,x_4=x_2^2,x_5=x_1\cdot x_2,$ 於是上式化為五元一次線性回歸方程：

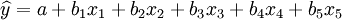
　　 $\widehat{y}=a+b_1x_1+b_2x_2+b_3x_3+b_4x_4+b_5x_5$

　　這樣以來，便可按多元線性回歸分析的方法，計算各偏回歸繫數，建立二元二次多項式回歸方程。

多元非線性回歸分析模型^[1]

　　一、常見的內蘊多元性回歸模型

　　只要對模型中的變數進行數學變換，比如自然對數變換等，就可以將其轉化具有標準形式特征的多元線性回歸模型。

　　1.多重彈性模型

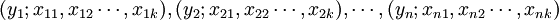　　 $(y_1;x_{11},x_{12}\cdots,x_{1k}),(y_2;x_{21},x_{22}\cdots,x_{2k}),\cdots,(y_n;x_{n1},x_{n2}\cdots,x_{nk})$ 是一組對的樣本觀察資料，則稱存在下列關係的非線性回歸模型為多重彈性模型

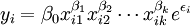　　 $y_i=\beta_0x_{i1}^{\beta_1}x_{i2}^{\beta_2}\cdots x_{ik}^{\beta_k}e^{\epsilon_{i}}$ 　　(1)

　　上述模型中的各解釋變數的冪，能夠說明解釋變數的相對變化對被解釋變數產生的相對影響，我們正式從這一角度說它是多重彈性模型的。

　　2.Cobb-Dauglas生產函數模型

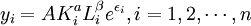　　 $y_i=AK_{i}^aL_i^{\beta}e^{\epsilon_{i}},i=1,2,\cdots,n$ 　　(2)

　　其中， $y i$ 表示產出總量， $K i$ 為資本要素， $L i$ 為勞動力要素，A、α、β為參數。比較式(1)和(2)，不難看出C-D生產函數模型實際是多重彈性模型的簡化或特殊形式。

　　3.總成本函數模型

　　用 $y i$ 表示總成本， $x i$ 表示產出規模，則稱具有如下關係的回歸模型為總成本函數模型

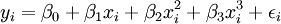　　 $y_i=\beta_0+\beta_1x_i+\beta_2x_i^2+\beta_3x_i^3+\epsilon_i$ ,i=1,2,…,n　　(3)

　　總成本函數是多項式函數的特殊形式，更為一般的情況就是多項式回歸模型：

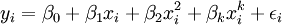　　 $y_i=\beta_0+\beta_1x_i+\beta_2x_i^2+\beta_kx_i^k+\epsilon_i$ ,i=1,2,…,n　　　(4)

　　多項式回歸模型從寬鬆的角度講，可以不把它看成是非線性回歸模型，在這裡主要是用來說明一下問題，把它看成內蘊的線性回歸模型也無妨。

　　二、內蘊的非線性回歸模型

　　內蘊非線性回歸模型的形式有很多種，大部分難以根據經濟含義進行稱呼，下麵，列出幾個以幫助大家增加認識。

　　(1)CES生產函數模型

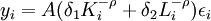　　 $y_i=A(\delta_1K_i^{-\rho}+\delta_2L_i^{-\rho})\epsilon_i$ ,i=1,2,…,n　　(5)

　　(2)隨機項表現為加法的C-D生產函數模型

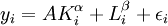　　 $y_i=AK_i^\alpha+L_i^\beta+\epsilon_i$ ,i=1,2,…,n　　(6)

　　(3)其他形式的內蘊非線性函數模型，如

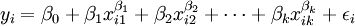　　 $y_i=\beta_0+\beta_1x_{i1}^{\beta_{1}}+\beta_2x_{i2}^{\beta_{2}}+\cdots+\beta_kx_{ik}^{\beta_{k}}+\epsilon_i$ ,i=1,2,…,n　　(7)

　　三、多元非線性回歸模型的求解問題

　　對內蘊的線性回歸模型，可以通過對模型中的變數或樣本數據進行變換，將其轉化成具有標準線性形式特征的回歸模型，然後再運用前面介紹的模型估計方法進行估計，便能間接地達到目的。比如對於式(2)，它的變換過程為

　　對式(2)兩邊求對數

　　 $ln y i = l n A + α l n K i + β l n L i + ε i$

　　令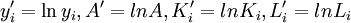 $y^\prime_i=\ln y_i,A^\prime=ln A,K_i^\prime=ln K_i,L_i^\prime=ln L_i$ ,則得

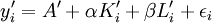　　 $y^\prime_i=A^\prime+\alpha K_i^\prime+\beta L_i^\prime+\epsilon_i$ ,i=1,2,…,n

　　這是標準的二元線性回歸問題，可據之估計出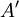 $A^\prime$ 、α和β.

參考文獻

↑ 耿修林.商務經濟統計學[M].科學出版社,2003年11月第1版.

取自"https://wiki.mbalib.com/zh-tw/%E5%A4%9A%E5%85%83%E9%9D%9E%E7%BA%BF%E6%80%A7%E5%9B%9E%E5%BD%92%E5%88%86%E6%9E%90"

打开MBA智库App, 阅读完整内容打开App

如果您認為本條目還有待完善，需要補充新內容或修改錯誤內容，請編輯條目或投訴舉報。

本条目由以下用户参与贡献

Yixi,林巧玲.

頁面分類: 決策預測

評論(共0條)

提示:評論內容為網友針對條目"多元非線性回歸分析"展開的討論，與本站觀點立場無關。

發表評論請文明上網，理性發言並遵守有關規定。

以上内容根据网友推荐自动排序生成

闽公网安备 35020302032707号