CES生產函數

用手机看条目

出自 MBA智库百科(https://wiki.mbalib.com/)

CES生產函數(Constant Elasticity of Substitution)

什麼是CES生產函數^[1]

　　CES生產函數是指替代彈性為常數的，CES生產函數首先由Solow提出的，經過實證檢定，逐漸被應用。

[編輯]

CES生產函數的公式^[2]

　　CES生產函數為常替代彈性生產函數

　　 $Y = A (δ 1 k - ρ + δ 2 L - ρ) 1 / ρ$ 　　　　(1)

　　的簡稱, 這是因為式(1)所表示的生產函數的替代彈性

　　 $σ = 1 / (1 + ρ)$ 為常數。

　　在經濟理論中,生產函數Y=F(K,L)應滿足:對任意的K、L有，Y(0,L)=Y(K,0)=0。

　　有些生產函數例如C－D函數

　　 $Y = A K α L β$ ,則由其函數表達式自然滿足Y(0,L)=Y(K,0)=0,即為預設。

　　在研究CES生產函數時, 必須同時準確地給出其使用條件:

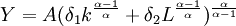
　　 $Y=A(\delta_1 k^{\frac{\alpha-1}{\alpha}}+\delta_2 L^{\frac{\alpha-1}{\alpha}})^{\frac{\alpha}{\alpha-1}}$

　　其中K>O 且L>0。

[編輯]

CES生產函數的性質^[2]

　　由以上討論,我們首先給出CES生產函數(l)的定義域為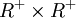 $R^+\times R^+$

　　對於固定的L>0,由(1)式可得人均產出函數

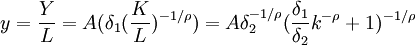
　　 $y=\frac{Y}{L}=A(\delta_1(\frac{K}{L})^{-1/\rho})=A\delta_2^{-1/\rho}(\frac{\delta_1}{\delta_2}k^{-\rho}+1)^{-1/\rho}$

　　記為y=f(k)　　　　(2)

　　這裡k=K/L表示人均資本(或稱勞動裝備)。

　　對(2)求導,得

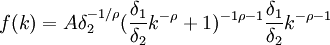　　 $f(k)=A\delta_2^{-1/\rho}(\frac{\delta_1}{\delta_2}k^{-\rho}+1)^{-1\rho-1 }\frac{\delta_1}{\delta_2}k^{-\rho-1}$ 　　　　(3)

　　顯然,當k>0且L>O時,有

　　性質1，人均CES生產函數(2)在其定義域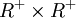 $R^+\times R^+$ 內,恆有

　　f(k)>0

　　再對(3)式求導，得

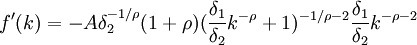　　 $f'(k)=-A\delta_2^{-1/\rho}(1+\rho)(\frac{\delta_1}{\delta_2}k^{-\rho}+1)^{-1/\rho-2}\frac{\delta_1}{\delta_2}k^{-\rho-2}$ 　　　　(4)

　　由此又有

　　性質2，人均CES生產函數(2)在其定義域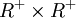 $R^+\times R^+$ 內,恆有

　　f(k)<0

　　由性質1、性質2知,人均CES生產函數(2)為凹函數。

　　性質1的經濟意義為:邊際產出大於零,即資本k每增加一個單位,則產出y增加

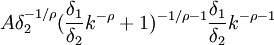　　 $A\delta_2^{-1/\rho}(\frac{\delta_1}{\delta_2}k^{-\rho}+1)^{-1/\rho-1}\frac{\delta_1}{\delta_2}k^{-\rho-1}$ 個單位

　　性質2說明人均CES生產函數從經濟上來說是規模遞減的,即隨資本k的增加,邊際產出遞增的速度下降。

[編輯]

CES生產函數的運用^[2]

　　假設考慮三種生產要素的CES函數,即固定資本品 $K 1$ 、中間消耗品 $K 2$ 和勞動力L,並假設勞動力L在考察期內不變,即具有以下的生產函數形式:

　　 $Y_1=A[\delta_1K_1^{\rho}+\delta_2K_2{\rho}+\delta_3L^\rho]^\frac{1}{\rho},0<\delta_i<1,i=1,2,A>0,\rho<1$ 　　　　（5）

　　在封閉的經濟中第t+1年固定資本品投人來源於第t年的剩餘和第t年產出的再投入部分,比例為 $σ 1$ ,第t+1年中間消耗來源於第t年產出的投人,比例為 $σ 2$ ,第t年消費均來自當年的產出扣除下一年的再投人部分。

　　假設折舊率為 $μ$ ,整個社會的消費記為C(t),人均消費記為c(t),如上兩邊同除L,人均化後即有:

　　 $y_1=A[\delta_1K_1^{\rho}+\delta_2k_2^{\rho}+\delta_3]^{\frac{1}{\rho}},0<\delta_i,i=1,2,A>0,\rho<1$ 　　　　(6)

　　且有如下關係:

　　 $k 1 (t + 1) = k 1 (t) - μ k 1 (t) + σ 1 y (t)$

　　 $k 2 (t + 1) = σ 2 y (t)$ 　　　　　　　　　　　　(7)

　　 $c (t) = (1 - σ 1 - σ 2) y (t)$

　　取考察期內的人均消費的效用達到最大化,我們建立的模型如下:

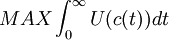
　　 $MAX\int_0^{\infty}U(c(t))dt$

　　 $y(t)=A[\delta_1k_1^{\rho}+\delta_2k_2^{\rho}+\delta_3]^{\frac{1}{\rho}}$

　　 $k 1 (t + 1) = k 1 (t) - μ k 1 (t) + σ 1 y (t)$ 　　　　　　　　　　(8)

　　 $c (t) = (1 - σ 1 - σ 2) y (t),0 < δ i < 1, i = 1,2;0 < μ < 1$

　　把狀態方程(7)連續化得到:

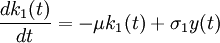　　 $\frac{dk_1(t)}{dt}=-\mu k_1(t)+\sigma_1 y(t)$ 　　　　(9)

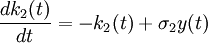
　　 $\frac{dk_2(t)}{dt}=-k_2(t)+\sigma_2 y(t)$ 　　　　　　

　　對系統(9),均衡時由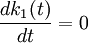 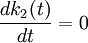$\frac{dk_1(t)}{dt}=0$ , $\frac{dk_2(t)}{dt}=0$ 解得惟一的正均衡點 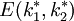$E(k_1^{*},k_2^{*})$ 滿足：

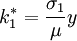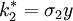　　 $k_1^{*}=\frac{\sigma_1}{\mu}y$ , $k_2^{*}=\sigma_2y$ 　　　　(10)

　　把它們帶人生產函數的表達式中得到：

　　 $y=A[\delta_1(\frac{\sigma_1}{\mu}y)^{\rho}+\delta_2(\sigma_2y)^{\rho}+\delta_3]^{\rho}$

　　可解得在均衡點處有：

　　 $y^*=[\frac{1}{\delta_3}(\frac{1}{A})^{\rho}-\frac{\delta_1}{\delta_3}(\frac{\sigma_1}{\mu})^{\rho}-\frac{\delta_2}{\delta_3}\sigma_2^{\rho}]^{\frac{1}{\rho}}$ 　　　　(11)

　　再把它帶人式(10)中就有:

　　 $k_1^{*}=\frac{\sigma_1}{\mu}[\frac{1}{\delta_3}(\frac{1}{A})^{\rho}-\frac{\delta_1}{\delta_3}(\frac{\sigma_1}{\mu})^{\rho}-\frac{\delta_2}{\delta_3}\sigma_2^{\rho}]^{\frac{1}{\rho}}$

　　 $k_2^{*}=\sigma_2[\frac{1}{\delta_3}(\frac{1}{A})^{\rho}-\frac{\delta_1}{\delta_3}(\frac{\sigma_1}{\mu})^{\rho}-\frac{\delta_2}{\delta_3}\sigma_2^{\rho}]^{\frac{1}{\rho}}$

　　我們可以得到在均衡點的導繫數矩陣為

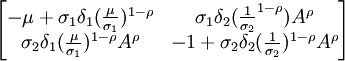
　　 $\begin{bmatrix} -\mu+\sigma_1 \delta_1(\frac{\mu}{\sigma_1})^{1-\rho} & \sigma_1 \delta_2(\frac{1}{\sigma_2}^{1-\rho})A^{\rho} \\ \sigma_2 \delta_1(\frac{\mu}{\sigma_1})^{1-\rho}A^{\rho} & -1+\sigma_2 \delta_2(\frac{1}{\sigma_2})^{1-\rho}A^{\rho}\end{bmatrix}$

　　容易得到其特征方程為:

　　 $\lambda^2-[\sigma_1\delta_1(\frac{\mu}{\sigma_1})^{1-\rho}A^{\rho}-\mu +\sigma_2\delta_2(\frac{1}{\sigma_2})^{1-\rho}A^{\rho}-1]\lambda$

　　 $+[\mu -\sigma_1\delta_1(\frac{\mu}{\sigma_1})^{1-\rho}A^{\rho}-\mu \sigma_2 \delta_2(\frac{1}{\sigma_2})^{1-\rho}A^{\rho}]$

　　根據根與繫數的關係, 我們很容易得到:

　　(1)若 $ρ 2$ > $4 q$ >0,且 $ρ$ >0,則 $λ 1$ , $λ 2$ >0,即下列條件成立：

　　 $μ - δ 1 μ 1 - ρ (A σ 1) ρ - μδ 2 (A σ 2) ρ > 0$

　　 $δ 1 μ 1 - ρ (A σ 1)ρ + δ 2 (A σ 2) ρ - (μ + 1) > 0$

　　上述兩式相加可得到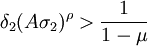 $\delta_2(A\sigma_2)^{\rho}>\frac{1}{1-\mu}$ 。此時系統均衡點是不穩定結。

　　而當 $ρ < 0$ ,則 $λ 1$ , $λ 2$ <0,亦即下列條件成立:

　　 $2μ + 1 > 2δ 1 μ 1 - ρ (A σ 1) ρ + (1 + μ)δ 2 (A σ 2) ρ$

　　此時系統均衡點是穩定結點。

　　(2)若 $ρ 2$ < $4 q$ ,當 $R e (λ) > 0$ 時,系統均衡點是不穩定結點。而當 $R e (λ) < 0$ 時,系統均衡點是穩定結點。

　　(3)若 $ρ < 0$ ,則一個根為正,另一個根為負,即下列條件成立:

　　 $1 < δ 1 μ - ρ (A σ 1) ρ + δ 2 (A σ 2) ρ$

　　此時均衡點為鞍點。有一枝分界線趨於均衡點E,這就是經濟學中所說的:只有惟一的最佳路徑穩定地趨於均衡點E。而另一枝分界線則離開均衡點E。其餘的軌線均從“最佳路徑”饒過均衡點而靠近另一枝分界線。亦即其相圖猶如馬鞍狀。

　　(4)若 $ρ = 0$ ,即下列條件成立: $μ = δ 1 μ 1 - ρ (A σ 1) ρ - μδ 2 (A σ 2) ρ$ ，則此時系統均衡點為高階的,我們不做研究。

[編輯]

參考文獻

↑ 蔣文蔚編著.微觀經濟數量分析.中國物價出版社,2001.09.
↑ ^2.0 ^2.1 ^2.2 嚴忠,江海峰.CES生產函數及其運用[J].數量經濟技術經濟研究,2002,(第9期).

取自"https://wiki.mbalib.com/zh-tw/CES%E7%94%9F%E4%BA%A7%E5%87%BD%E6%95%B0"

打开MBA智库App, 阅读完整内容打开App

如果您認為本條目還有待完善，需要補充新內容或修改錯誤內容，請編輯條目或投訴舉報。

本条目由以下用户参与贡献

yanfei,林巧玲,Mis铭.

頁面分類: 經濟學術語

評論(共3條)

提示:評論內容為網友針對條目"CES生產函數"展開的討論，與本站觀點立場無關。

140.118.226.* 在 2014年11月16日 05:31 發表

最上面的elasticity拼錯啦呵呵

回複評論

Mis铭 (討論 | 貢獻) 在 2014年11月17日 09:38 發表

140.118.226.* 在 2014年11月16日 05:31 發表

最上面的elasticity拼錯啦呵呵

謝謝指正，已經修改！MBA智庫百科是可以自由修改編輯的，您也可以直接參与！

回複評論

140.112.177.* 在 2016年11月4日 16:48 發表

Y = A(δ1k − ρ + δ2L − ρ)1 / ρ　　　　(1) 是不是要改成 Y = A(δ1k − ρ + δ2L − ρ)-1 / ρ才對?

回複評論

發表評論請文明上網，理性發言並遵守有關規定。

查看

工具▼

CES生產函數

出自 MBA智库百科(https://wiki.mbalib.com/)

目錄

什麼是CES生產函數^[1]

CES生產函數的公式^[2]

CES生產函數的性質^[2]

CES生產函數的運用^[2]

參考文獻

温馨提示

本条目相关课程

本条目由以下用户参与贡献

評論(共3條)

導航

意见反馈

查看

工具▼

CES生產函數

出自 MBA智库百科(https://wiki.mbalib.com/)

目錄

什麼是CES生產函數[1]

CES生產函數的公式[2]

CES生產函數的性質[2]

CES生產函數的運用[2]

參考文獻

温馨提示

本條目相關文檔

本条目相关课程

本条目由以下用户参与贡献

評論(共3條)

導航

意见反馈

什麼是CES生產函數^[1]

CES生產函數的公式^[2]

CES生產函數的性質^[2]

CES生產函數的運用^[2]