免疫策略
出自 MBA智库百科(https://wiki.mbalib.com/)
免疫策略(Immunization Strategy)
目錄 |
免疫策略是對債券投資組合進行管理的策略之一，是指債券組合管理者不積極尋求交易的可能性而企圖戰勝市場的一種消極策略。它的基本假設是，債券市場是半強型有效的市場，債券的現時價格能準確地反映所有能公開獲得的信息。免疫策略能夠保護債券組合避免遭受利率風險變動造成的損失。管理者通過選擇麥考利久期等於其負債(現金流出)的到期期限的債券組合，利用價格風險和再投資風險相互抵消的特點，可以保證一定時期後獲得固定的現金流。
債券投資組合的麥考利久期等於組合內各種債券麥考利久期的加權平均值，即
式中，Dp——債券投資組合的麥考利久期。
wi——債券i在債券投資組合中的比例。
Di——債券i的麥考利久期。
n——債券組合中債券的種數。
建立免疫債券投資組合的目標是找到一個麥考利久期等於其負債(現金流出)的到期期限的債券組合，其核心問題是確定債券投資組合中各種債券的投資比重。利用Excel的規劃求解工具可以很方便地解決這類問題。
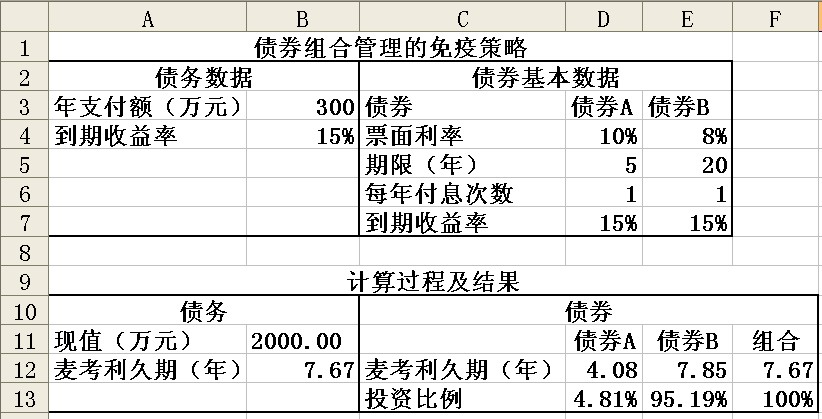
【例】某基金管理公司已建立一個養老基金，其債務是每年向受益人支付300萬元，永不終止。基金管理者計劃建立一個債券組合來滿足這個要求，所有債券的到期收益率均為15％。如果債券組合由債券A和債券B組成，債券A的票面利率10％、期限5年、每年付息一次；債券B的票面利率8％、期限20年、每年付息一次。那麼，要使債務完全免疫，每種債券的持有量為多少?
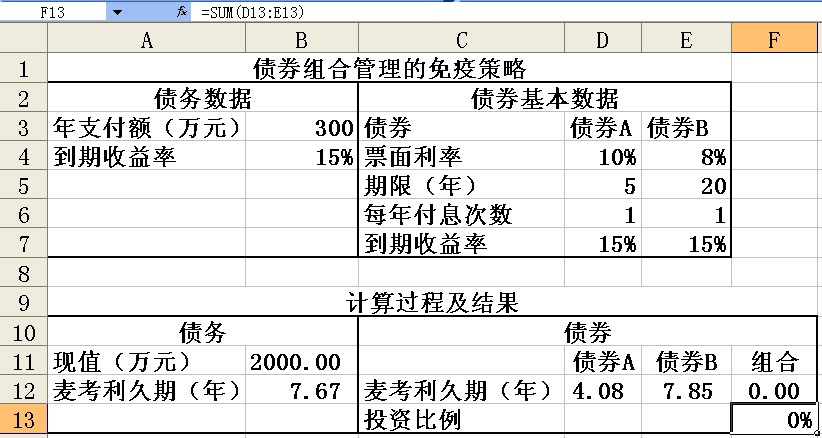
如圖所示，計算步驟如下：
(1)在單元格B11中輸入公式“=B3/B4”，計算債務的現值。在單元格B12中輸入公式“=(1+B4)/B4”，計算債務的麥考利久期。
(2)在單元格D12中輸入公式“=DURATION("2000/1/1",2000+D5&"/1/1",D4,D7,D6)”；在單元格E12中輸入公式=DURATION("2000/1/1",2000+E5&"/1/1",E4,E7,E6)，計算債券A和債券B的麥考利久期。
(3)在單元格F12中輸入公式“=SUMPRODUCT(D12:E12,D13:E13)”，計算債券組合的久期。
(4)在單元格F13中輸入公式“=SUM(D13:E13)”。
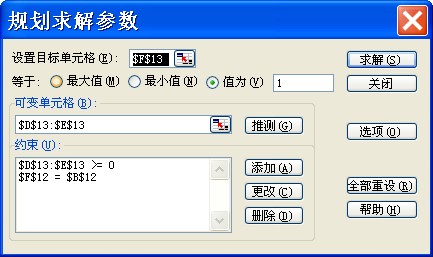
(5)單擊【工具】菜單中的【規劃求解】命令，打開【規劃求解參數】對話框，在【設置目標單元格】中輸入“$F$13”：【等於】選擇“值為1”：(可變單元格]中輸入“$D$13:$E$13”：在【約束】中添加以下的約束條件：“$F$12=$B$12”、“$D$13：$E$13>=0”，然後單擊【求解】按鈕，則可得最終計算結果如圖所示。可見，債券組合中，債券A的比例為4.81％，債券B的比例為95.19％。
選擇這樣的債券組合進行投資，即可以滿足無限期地每年向養老金的受益人支付300萬元的需求。[1]
免疫策略的分類[2]
利率風險包括價格風險和再投資風險。債券的價格與利率變化呈反向變動。當利率上升(下降)時，債券的價格便會下跌(上漲)。對於持有債券直至到期的投資者來說，到期前債券價格的變化沒有什麼影響；但是，對於在債券到期日前出售債券的投資者而言，如果購買債券後市場利率水平上升，債券的價格將下降，投資者將遭受資本損失。這種風險就是利率變動產生的價格風險。利率變動導致的價格風險是債券投資者面臨的最主要風險。利息的再投資收入的多少主要取決於再投資發生時的市場利率水平。如果利率水平下降，獲得的利息只能按照更低的收益率水平進行再投資，這種風險就是再投資風險。債券的持有期限越長，再投資的風險就越大；在其他條件都一樣的情況下，債券的票面利率越高，債券的再投資風險也越大。
利率波動對債券價格和再投資收入的影響正好相反：當利率上升時，債券的價格將下跌，但是債券的再投資收入將增加；當利率下降時，債券價格將上漲，但是債券的再投資收入將會下降。可以通過將資產負債期限進行適當的搭配使兩種利率風險正好相互抵消，從而消除債券組合的利率風險。這正是免疫策略的基本思想。
為了理解免疫策略背後的基本思想，先考察一種最簡單的情況：目標期免疫策略，即某金融機構在未來某個時期需要支付一筆確定現金流，現在該金融機構應該如何構造債券組合以規避利率風險。
【例】某銀行發行面值為10000元的定期存單，該存單期限為5年，年利率為8％，複利計息，該銀行5年後需支付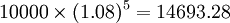
(元)。為了保證5年後有足夠的資金償還該定期存單所形成的債務，該銀行購買了按面值出售的10000元債券，債券的年利率為8％，6年後到期。由計算可知，該債券的持續期（麥考利久期）為5年，該銀行5年後將債券銷售以獲得支付債務所需的資金。假設收益率曲線是水平的，並且只能平行移動。考察銀行購買債券後利率變化的三種情況：一是利率始終保持在8％的水平；二是利率降為7％並維持不變；三是利率上升到9％並保持不變。
- 以第一種情況為例說明如何計算5年後債券的終值。
- 在第一年年底債券支付利息10000×8％=800 (元)，該筆現金流還可以按照8Vo的年利率再投資4年，終值為
(元)；
- 在第二年年底債券支付利息10000×8％=800(元)，該筆現金流還可以按照8％的年利率再投資3年，終值為
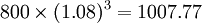(元)。
- 以此類推，到第5年獲得利息800元．同時將債券按照當時的價格銷售出去。
- 債券5年後的銷售價格等於第6年發生的現金流的貼現值10800÷(1+8％)=10000 (元)。
- 將上述所有現金流在第5年的終值加總等於14693.28元。
三種情況下5年後債券終值的計算如表所示。
表 5年後債券的終值
| 時間(年) | 現金流 | 8％(r) | 7％(r) | 9％(r) |
|---|---|---|---|---|
| 1 | 800 | 1088.39 | 1048.64 | 1129.27 |
| 2 | 800 | 1007.77 | 980.03 | 1036.02 |
| 3 | 800 | 933.12 | 915.92 | 950.48 |
| 4 | 800 | 864.00 | 856.00 | 872.00 |
| 5 | 800 | 800.00 | 800 | 800 |
| 利息總收入 | 4693.28 | 4600.59 | 4787.77 | |
| 5年後債券價格 | 10000 | 10093.46 | 9908.26 | |
| 5年後債券組合終值 | l4693.28 | 14694.05 | 14696.02 | |
通過表可以清楚地看到，利率從8％降到7％，債券的利息再投資收入減少了4693.28-4600.59=92.69 (元)，但是銷售價格卻從10000元漲到10093.46元，二者基本相互抵消。當利率從8％上漲到9％時，利息收入的增加基本上被價格的降低所抵消。因此，從上述例子可以看出，不論利率如何變化，再投資風險和價格風險相互抵消，債券組合的利率風險被消除了。
在上述例子中，銀行規避利率風險的機制是什麼?首先，銀行的資產和負債的現值(市場價值)相等，都是10000元；其次，資產和負債的持續期相等，都是5年。上述兩個條件就能保證投資者到期有足夠的資金滿足償還單筆債務的需要。因此，目標期免疫策略規避利率風險的兩個條件是：①債券組合和負債的現值相等。②債券組合和負債的持續期相等。
養老基金和壽險公司等金融機構未來需要償付一系列的現金流以滿足養老基金受益人和投保人的需要。金融機構可以採用多期免疫策略實現對多期負債的免疫。
多期免疫是指不論利率如何變化，通過構建某種債券組合以滿足未來一系列負債產生的現金流支出需要。可以通過兩種方法實現多期免疫策略：
- 一是將每次負債產生的現金流作為一個單期的負債，然後利用上述目標期免疫策略針對每次負債分別構建債券組合，令債券組合的持續期和現值與各期負債的持續期和現值相等；
- 二是構建債券組合，令債券組合的持續期與負債現金流的持續期加權平均值相等。例如，如果一家養老基金在4年、5年和6年後需支付3筆資金，每筆資金的現值都是100萬元。為了對這3筆負債進行免疫，該養老基金既可以投資於3種債券(組合)，每種債券(組合)的現值都是100萬元，持續期分別是4年、5年和6年；也可以投資於持續期等於5年的債券組合，因為負債的持續期加權平均數等於5年，計算如下：
(年)
後一種方法債券組合構造和管理都相對簡單。但是理論研究表明資產和負債的持續期相等並不能保證完全免疫，因此，最好的多期免疫策略仍然是第一種方法。
評論(共3條)
樓上的，你的理解有誤 投資的2000萬是現值，你需要將那兩個債券的現值算出來，用上述比例的投資總額現值計算持有對應債券的數量，用數量乘以債券的面值再乘票息率，猜得到每年獲得票息。 例如投向5年期的總額是2000*0.481=96.2W，但是因為這個債券目前價格是83.23922451，所以能買到11581.07858張面值100的債券，用這個票麵價值乘以10%，才是每年得到的票息。 而20年的職權，目前價格僅有56.18467968
你可以繼續算下去，雖然還是有差異，但是差異在6%以下，可以認為是數據截尾造成的問題了。
根據免疫策略求解事例，基金公司每年付300支付額的那個，得出的結果與預計不同， 根據事例結果投資債券A比例為4.81%，債券利息收入10%也就是說債券A的投資收入為2000*4.81%*10%=9.62，同理，債券B的收入為2000*95.19%*8%=152.304,這隻債券組合收入為161.924與300的支付額有一定差距。 這個是因為我理解有錯誤，還是因為演算法有錯誤，還是這個例子本身就是個不能存在的命題，請指教