持續期
出自 MBA智库百科(https://wiki.mbalib.com/)
持續期(Duration)
目錄 |
持續期(Duration)也稱久期,最初由美國經濟學家弗雷德里克-麥克萊(F.R.Macaulay)於1936年提出。持續期作為一種全新的概念在當時出現,使人們對固定收入金融工具的實際償還期與風險的關係有了更深入的瞭解,同時被廣泛地用於預測由於市場利率變動所引起的債券價格的變動。20世紀80年代以來,持續期又被金融機構運用於資產負債管理之中。
從經濟涵義上講,持續期是固定收入金融工具現金流的加權平均時間,也可以理解為金融工具各期現金流抵補最初投入的加權平均時間。在計算中,麥克萊持續期的一般表達式為,金融工具各期現金流發生的相應時間乘以各期現金流現值之和與該金融工具總現值的商,即
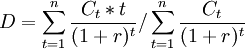
D為持續期;t為各現金流發生時間;Ct金融工具第t期現金流;r為市場利率;設Ct / (1 + r)t = pvt,則有:
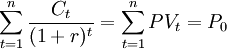
持續期公式可以寫成:
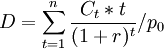
如果把固定收入債券各期將收回的現金流的現值表示為金融工具總現值P0的一部分,即作為一種各期將收回的現金流的現值占總現值,或最初總投入的權重則公式可變形為:
![D=\sum_{t=1}^n PV_t*t / p_0=\sum_{t=1}^n \left[ {PV_t \over p_0}*t \right]=\sum_{t=1}^n \left[ W_t \times t \right]](/w/images/math/9/d/b/9db15bea3a2fece7f1752ce67a474408.png)
上式把各期現金流的現值表示為金融工具總現值P0的一部分,即各期現金流現值占該金融工具總現值的比例,其和等於1。把這些比率作為權重(wt)分別乘以各期現金流發生的時間,就得到該項金融工具的持續期。持續期在經濟意義上還可以理解為該項金融工具各期現金流抵補最初投入的加權平均時間。
持續期還有一種近似表達:
![D\approx\left[{\triangle P \over p}/{\triangle r \over (1+r)} \right]](/w/images/math/f/4/7/f47a0727180fd9254023b246403fd4e4.png)
P為金融工具購買時市場價格;△P為金融工具價格變動;r為金融工具購入時市場利率;△r為市場利率變動。
上式可以理解為金融工具的價格彈性,即市場利率變動的百分比所引起金融工具價格變動百分比的關係。由於利率變動對固定收入的金融工具價格變動的影響是反向的,故其變動關係用負數表示。上式經過變形,可以引出計算金融工具價格變動的近似表達式:
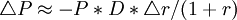
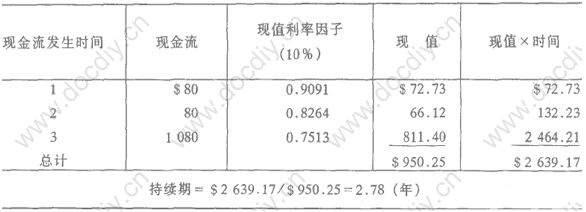
例:設某固定收入債券的息票為每年80美元,償還期為3年,面值為1000美元。該金融工具的實際收益率(市場利率)為10%,現行市場價格為 950.25美元,求該債券的持續期。在持續期計算中,先計算每期現金流的現值,然後每個現值乘以相應的發生時間,再把各項乘積相加,並除以該債券的市場價格,就得到該債券的持續期為2.78年。見下表:








good for me