无广告阅读 
免验证复制 
微信支付 
支付宝 
PayPal 持续期
出自 MBA智库百科(https://wiki.mbalib.com/)
持续期（Duration）
目录[隐藏] |
持续期（Duration）也称久期，最初由美国经济学家弗雷德里克-麦克莱(F.R.Macaulay)于1936年提出。持续期作为一种全新的概念在当时出现，使人们对固定收入金融工具的实际偿还期与风险的关系有了更深入的了解，同时被广泛地用于预测由于市场利率变动所引起的债券价格的变动。20世纪80年代以来，持续期又被金融机构运用于资产负债管理之中。
从经济涵义上讲，持续期是固定收入金融工具现金流的加权平均时间，也可以理解为金融工具各期现金流抵补最初投入的加权平均时间。在计算中，麦克莱持续期的一般表达式为，金融工具各期现金流发生的相应时间乘以各期现金流现值之和与该金融工具总现值的商，即
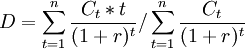
D为持续期；t为各现金流发生时间；Ct金融工具第t期现金流；r为市场利率；设Ct / (1 + r)t = pvt，则有：
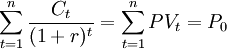
持续期公式可以写成：
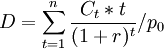
如果把固定收入债券各期将收回的现金流的现值表示为金融工具总现值P0的一部分，即作为一种各期将收回的现金流的现值占总现值，或最初总投入的权重则公式可变形为：
![D=\sum_{t=1}^n PV_t*t / p_0=\sum_{t=1}^n \left[ {PV_t \over p_0}*t \right]=\sum_{t=1}^n \left[ W_t \times t \right]](/w/images/math/9/d/b/9db15bea3a2fece7f1752ce67a474408.png)
上式把各期现金流的现值表示为金融工具总现值P0的一部分，即各期现金流现值占该金融工具总现值的比例，其和等于1。把这些比率作为权重（wt）分别乘以各期现金流发生的时间，就得到该项金融工具的持续期。持续期在经济意义上还可以理解为该项金融工具各期现金流抵补最初投入的加权平均时间。
持续期还有一种近似表达：
![D\approx\left[{\triangle P \over p}/{\triangle r \over (1+r)} \right]](/w/images/math/f/4/7/f47a0727180fd9254023b246403fd4e4.png)
P为金融工具购买时市场价格；△P为金融工具价格变动；r为金融工具购入时市场利率；△r为市场利率变动。
上式可以理解为金融工具的价格弹性，即市场利率变动的百分比所引起金融工具价格变动百分比的关系。由于利率变动对固定收入的金融工具价格变动的影响是反向的，故其变动关系用负数表示。上式经过变形，可以引出计算金融工具价格变动的近似表达式：
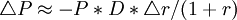
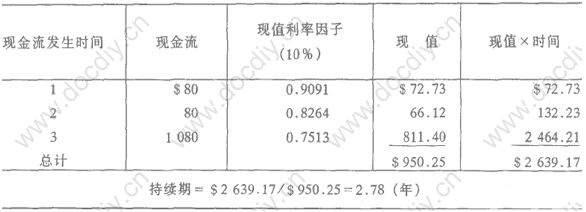
例：设某固定收入债券的息票为每年80美元，偿还期为3年，面值为1000美元。该金融工具的实际收益率（市场利率）为10%，现行市场价格为 950.25美元，求该债券的持续期。在持续期计算中，先计算每期现金流的现值，然后每个现值乘以相应的发生时间，再把各项乘积相加，并除以该债券的市场价格，就得到该债券的持续期为2.78年。见下表:
本条目相关课程
good for me