主成分分析法
出自 MBA智库百科(https://wiki.mbalib.com/)
主成分分析(principal components analysis,PCA)又稱:主分量分析,主成分回歸分析法
目錄 |
主成分分析也稱主分量分析,旨在利用降維的思想,把多指標轉化為少數幾個綜合指標。
在統計學中,主成分分析(principal components analysis,PCA)是一種簡化數據集的技術。它是一個線性變換。這個變換把數據變換到一個新的坐標系統中,使得任何數據投影的第一大方差在第一個坐標(稱為第一主成分)上,第二大方差在第二個坐標(第二主成分)上,依次類推。主成分分析經常用減少數據集的維數,同時保持數據集的對方差貢獻最大的特征。這是通過保留低階主成分,忽略高階主成分做到的。這樣低階成分往往能夠保留住數據的最重要方面。但是,這也不是一定的,要視具體應用而定。
在實證問題研究中,為了全面、系統地分析問題,我們必須考慮眾多影響因素。這些涉及的因素一般稱為指標,在多元統計分析中也稱為變數。因為每個變數都在不同程度上反映了所研究問題的某些信息,並且指標之間彼此有一定的相關性,因而所得的統計數據反映的信息在一定程度上有重疊。在用統計方法研究多變數問題時,變數太多會增加計算量和增加分析問題的複雜性,人們希望在進行定量分析的過程中,涉及的變數較少,得到的信息量較多。主成分分析正是適應這一要求產生的,是解決這類題的理想工具。
同樣,在科普效果評估的過程中也存在著這樣的問題。科普效果是很難具體量化的。在實際評估工作中,我們常常會選用幾個有代表性的綜合指標,採用打分的方法來進行評估,故綜合指標的選取是個重點和難點。如上所述,主成分分析法正是解決這一問題的理想工具。因為評估所涉及的眾多變數之間既然有一定的相關性,就必然存在著起支配作用的因素。根據這一點,通過對原始變數相關矩陣內部結構 的關係研究,找出影響科普效果某一要素的幾個綜合指標,使綜合指標為原來變數的線性擬合。這樣,綜合指標不僅保留了原始變數的主要信息,且彼此間不相關,又比原始變數具有某些更優越的性質,就使我們在研究複雜的科普效果評估問題時,容易抓住主要矛盾。 上述想法可進一步概述為:設某科普效果評估要素涉及個指標,這指標構成的維隨機向量為。對作正交變換,令其中為正交陣的各分量是不相關的,使得的各分量在某個評估要素中的作用容易解釋,這就使得我們有可能從主分量中選擇主要成分,削除對這一要素影響微弱的部分,通過對主分量的重點分析,達到對原始變數進行分析的目的。各分量是原始變數線性組合,不同的分量表示原始變數之間不同的影響關係。由於這些基本關係很可能與特定的作用過程相聯繫,主成分分析使我們能從錯綜複雜的科普評估要素的眾多指標中,找出一些主要成分,以便有效地利用大量統計數據,進行科普效果評估分析,使我們在研究科普效果評估問題中,可能得到深層次的一些啟發,把科普效果評估研究引向深入。
例如,在對科普產品開發和利用這一要素的評估中,涉及科普創作人數百萬人、科 普作品發行量百萬人、科普產業化(科普示範基地數百萬人)等多項指標。經過主成分分析計算,最後確定個或個主成分作為綜合評價科普產品利用和開發的綜合指標,變數數減少,並達到一定的可信度,就容易進行科普效果的評估。
主成分分析法是一種降維的統計方法,它藉助於一個正交變換,將其分量相關的原隨機向量轉化成其分量不相關的新隨機向量,這在代數上表現為將原隨機向量的協方差陣變換成對角形陣,在幾何上表現為將原坐標系變換成新的正交坐標系,使之指向樣本點散佈最開的p 個正交方向,然後對多維變數系統進行降維處理,使之能以一個較高的精度轉換成低維變數系統,再通過構造適當的價值函數,進一步把低維繫統轉化成一維繫統。
主成分分析的原理是設法將原來變數重新組合成一組新的相互無關的幾個綜合變數,同時根據實際需要從中可以取出幾個較少的綜合變數儘可能多地反映原來變數的信息的統計方法叫做主成分分析或稱主分量分析,也是數學上處理降維的一種方法。主成分分析是設法將原來眾多具有一定相關性(比如P個指標),重新組合成一組新的互相無關的綜合指標來代替原來的指標。通常數學上的處理就是將原來P個指標作線性組合,作為新的綜合指標。最經典的做法就是用F1(選取的第一個線性組合,即第一個綜合指標)的方差來表達,即Va(rF1)越大,表示F1包含的信息越多。因此在所有的線性組合中選取的F1應該是方差最大的,故稱F1為第一主成分。如果第一主成分不足以代表原來P個指標的信息,再考慮選取F2即選第二個線性組合,為了有效地反映原來信息,F1已有的信息就不需要再出現再F2中,用數學語言表達就是要求Cov(F1,F2)=0,則稱F2為第二主成分,依此類推可以構造出第三、第四,……,第P個主成分。[1]
概括起來說,主成分分析主要由以下幾個方面的作用。
1.主成分分析能降低所研究的數據空間的維數。即用研究m維的Y空間代替p維的X空間(m<p),而低維的Y空間代替 高維的x空間所損失的信息很少。即:使只有一個主成分Yl(即 m=1)時,這個Yl仍是使用全部X變數(p個)得到的。例如要計算Yl的均值也得使用全部x的均值。在所選的前m個主成分中,如果某個Xi的繫數全部近似於零的話,就可以把這個Xi刪除,這也是一種刪除多餘變數的方法。
2.有時可通過因數負荷aij的結論,弄清X變數間的某些關係。
3.多維數據的一種圖形表示方法。我們知道當維數大於3時便不能畫出幾何圖形,多元統計研究的問題大都多於3個變數。要把研究的問題用圖形表示出來是不可能的。然而,經過主成分分析後,我們可以選取前兩個主成分或其中某兩個主成分,根據主成分的得分,畫出n個樣品在二維平面上的分佈況,由圖形可直觀地看出各樣品在主分量中的地位,進而還可以對樣本進行分類處理,可以由圖形發現遠離大多數樣本點的離群點。
4.由主成分分析法構造回歸模型。即把各主成分作為新自變數代替原來自變數x做回歸分析。
5.用主成分分析篩選回歸變數。回歸變數的選擇有著重的實際意義,為了使模型本身易於做結構分析、控制和預報,好從原始變數所構成的子集合中選擇最佳變數,構成最佳變數集合。用主成分分析篩選變數,可以用較少的計算量來選擇量,獲得選擇最佳變數子集合的效果。
1、原始指標數據的標準化採集p 維隨機向量x = (x1,X2,...,Xp)T)n 個樣品xi = (xi1,xi2,...,xip)T ,i=1,2,…,n,
n>p,構造樣本陣,對樣本陣元進行如下標準化變換:
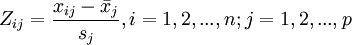
其中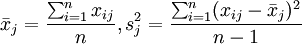 ,得標準化陣Z。
,得標準化陣Z。
2、對標準化陣Z 求相關係數矩陣
![R=\left[r_{ij}\right]_pxp=\frac{Z^T Z}{n-1}](/w/images/math/7/e/4/7e473cd0da3efb71ab376cb9ed048e72.png)
其中, 。
。
3、解樣本相關矩陣R 的特征方程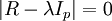 得p 個特征根,確定主成分
得p 個特征根,確定主成分
按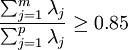 確定m 值,使信息的利用率達85%以上,對每個λj, j=1,2,...,m, 解方程組Rb = λjb得單位特征向量
確定m 值,使信息的利用率達85%以上,對每個λj, j=1,2,...,m, 解方程組Rb = λjb得單位特征向量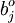 。
。
4、將標準化後的指標變數轉換為主成分
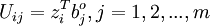
U1稱為第一主成分,U2 稱為第二主成分,…,Up 稱為第p 主成分。
5 、對m 個主成分進行綜合評價
對m 個主成分進行加權求和,即得最終評價值,權數為每個主成分的方差貢獻率。
優點:
①可消除評估指標之間的相關影響。因為主成分分析法在對原始數據指標變數進行變換後形成了彼此相互獨立的主成分,而且實踐證明指標間相關程度越高,主成分分析效果越好。
②可減少指標選擇的工作量,對於其他評估方法,由於難以消除評估指標間的相關影響,所以選擇指標時要花費不少精力,而主成分分析法由於可以消除這種相關影響,所以在指標選擇上相對容易些。
③主成分分析中各主成分是按方差大小依次排列順序的,在分析問題時,可以捨棄一部分主成分,只取前面方差較大的幾個主成分來代表原變數,從而減少了計算工作量。用主成分分析法作綜合評估時,由於選擇的原則是累計貢獻率≥85%,不至於因為節省了工作量卻把關鍵指標漏掉而影響評估結果。
缺點:
①在主成分分析中,我們首先應保證所提取的前幾個主成分的累計貢獻率達到一個較高的水平(即變數降維後的信息量須保持在一個較高水平上),其次對這些被提取的主成分必須都能夠給出符合實際背景和意義的解釋(否則主成分將空有信息量而無實際含義)。
②主成分的解釋其含義一般多少帶有點模糊性,不像原始變數的含義那麼清楚、確切,這是變數降維過程中不得不付出的代價。因此,提取的主成分個數m通常應明顯小於原始變數個數p(除非p本身較小),否則維數降低的“利”可能抵不過主成分含義不如原始變數清楚的“弊”。
③當主成分的因數負荷的符號有正有負時,綜合評價函數意義就不明確。
案例一:主成分分析法在啤酒風味評價分析中的應用[2]
啤酒是個多指標風味食品, 為了全面瞭解啤酒的風味, 啤酒企業開發了大量的檢測方法用於分析啤酒的指標, 但是面對大量的指標數據, 大多數企業又感到茫然,不知道如何利用這些大量的數據, 由上面的介紹可知,在這種情況下,主成分分析法能夠派上用場。近年來,科研人員為了獲得對啤酒風味更好的理解, 多元統計技術的使用越來越多。這主要有以下兩方面的原因:①在啤酒領域里, 幾乎沒有一個問題能夠使用單變數(單指標)就能反映事物的屬性, 例如啤酒的好壞、一致性, 不能通過雙乙酰一個指標說明問題;②另一個重要的原因就是, 近年來大量數學統計軟體的不斷出現和個人電腦的普及促進了多元統計分析技術的應用。多元統計技術在啤酒風味研究中的一個重要任務就是找出啤酒風格和啤酒理化指標(風味成分指標也屬於理化指標)之間的相關性。例如可以用多元統計技術來找出啤酒的風味指標和啤酒風味的關係或不同啤酒的風味差異性。
經常使用的多元統計技術有聚類分析、判別分析、主成分分析和回歸分析等。其中主成分分析能夠用於多指標產品, 主成分分析可以按照事物的相似性區分產品, 結果可用一維、二維或三維平面坐標圖標示, 特別直觀。使用主成分分析法可以研究隱藏在不同變數背後的關係,而且根據這些變數能夠獲得主成分的背景解釋。
鑒於主成分分析在啤酒風味質量應用中的強大作用, 本文簡單介紹主成分分析的基本原理及其在啤酒一致性監控中的應用,以引起我國啤酒同行的廣泛關註。
1.1 儀器
HP 6890 毛細管氣相色譜儀 (美國安捷倫公司),FID 檢測器, HP 7694E 頂空自動進樣器, HP 氣相色譜化學工作站。
1.2 分析方法
1.2.1 樣品製備
啤酒於5 ℃冷藏, 量取 5 mL 酒液於 20 mL 頂空瓶中, 添加2.0 g/L 正丁醇溶液 0.10 mL, 加密封墊及鋁蓋密封,振蕩混勻以供頂空氣相色譜測定。
1.2.2 色譜條件
毛細管色譜柱 (DB- WAXETR 30 m×0.53 mm i.d,膜厚1.0 μm);柱溫:起始溫度為 35 ℃, 以 10 ℃/min 程式升溫至150 ℃, 再以 20 ℃/min 升溫到180 ℃, 並繼續恆溫5 min;進樣口溫度 150 ℃; 檢測器溫度 200 ℃; 載氣為高純氮氣, 流速為5 mL/min;氫氣 30 mL/min;空氣400 mL/min;採用分流進樣,分流比為1∶1。
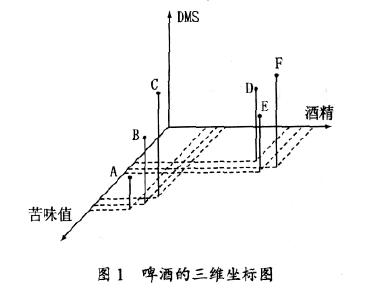
2.1 主成分分析法在啤酒研究中應用的必要性這裡通過一個例子說明, 主成分分析在啤酒研究中的必要性。假如有6 個啤酒樣品,分別標為A- F,每個啤酒樣品用3 個指標來描述。這些指標可以是儀器的分析數據、感官分析數據或兩者都用。為了便於討論,假設這3 個指標分別為苦味值(BU)、DMS和酒精濃度。為瞭解這6 個樣品兩兩之間的相似性, 便於將這6 個樣品進行分類,可以把這6 個樣品畫在三維空間中,見圖1。顯然在這個簡單的例子中, 這6 個樣品傾向於形成兩類, 即分別是A- C 和 D- F。通過所測的指標可以解釋這種分類, 例如, 第一組(A- C)有較高的苦味值和較低的酒精濃度。這個例子中只涉及到6 個樣品和3 個指標。但是實際上, 樣品數量和指標數量都會很大, 例如, 有20 個指標, 這時, 樣品不能在20 維的坐標系中畫出。為瞭解決多指標的樣品的比較問題,可以使用主成分分析法。
2.2 主成分分析法的基本原理
主成分分析的第一步是將所有的指標數據進行標準化, 標準化的一般方法為: (xij − xjmean) / δj, 這裡xij是樣品i 的第 j 個指標, xjmean 和 δj是第j 個指標的平均值和標準偏差, 通過標準化後, 每個變數的平均值變成0,標準偏差為1。標準化的好處是可以消除不同指標間的量綱差異和數量級間的差異。
第二步求出指標間的相關矩陣, 通過相關矩陣, 可以確定具有高度相關性的指標, 這些指標間的協方差可以通過另一個變數替代, 這個變數叫作第一成分。去掉第一成分後, 計算殘留相關陣, 通過殘留相關陣, 第二組高度相關的變數也可以發現, 它們的協方差可以用第二成分替代, 第二成分和第一成分是正交的。第二成分對原始數據的貢獻去除後, 可以提取第三成分。此過程一直繼續, 直到原始數據的所有方差都被提取後結束。結果是原數據轉化成了同樣數量的新變數, 但是, 這些新變數之間是正交的。
因此, 每個樣品的原始變數的標準化數據就被轉換成一系列成分的計算值。每一個樣品, 原始數據能夠表達成新成分的線性組合值, 例如一個有9 個指標的數據集就可轉換成:
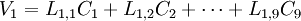
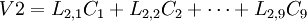
………………
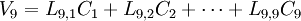
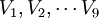 是原始數據的標準化值。
是原始數據的標準化值。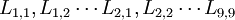 是原變數與新成分之間的相關程度的指標, 一般將其稱為因數荷載。
是原變數與新成分之間的相關程度的指標, 一般將其稱為因數荷載。
通過電腦的主成分程式生成對方差的貢獻率。一般而言, 原數據的總方差總是高度集中在前幾個成分中。因此,在這個分析中,可以基於可以接受的最低方差貢獻率,來選擇幾個數目較少的主成分。最終,可以用選擇的幾個主成分來重新計算所用的樣品。重新計算的值叫做主成分得分。
因為原始數據陣的方差通常集中在前幾個主成分中(一般為2 或 3 個), 因此樣品的一系列標準化因數得分可以在二維的平面坐標中畫出, 這樣就能夠根據樣品的相似性來分類樣品。另外, 還可以根據因數荷載對這種分類做出某種解釋。
3.1 主成分分析法在不同品牌啤酒風味差異性評價中的應用
啤酒是含酒精的飲料酒, 啤酒的風味是人們選擇啤酒的主要影響因素。顯然啤酒不同於同濃度的酒精水溶液, 主要是因為啤酒除了含有酒精外還含有數以百計的微量成分, 例如醛、醇及酯類等。對於啤酒生產企業來說, 把自己的啤酒和競爭啤酒的風味進行比較非常重要, 這樣可以瞭解自己的啤酒和競品的差異, 分析競爭啤酒受市場歡迎的原因, 以改進自己的產品, 或者找出自己啤酒的風格特點, 走差異化競爭之路。為了完成此工作, 啤酒企業可以把自己的啤酒和競爭啤酒進行對比品評, 這是一種非常好的方法, 但是此方法很難從本質上找到與競品的差異, 很難形成指導生產的定性定量措施。為瞭解決此問題, 啤酒企業可以對啤酒的風味成分進行分析, 理論上講, 分析的成分越多, 獲得的信息量越大, 但是, 很難從總體上進行對比分析, 這時, 可以通過主成分分析法, 提取主要的綜合成分, 然後在平面坐標系中畫圖進行比較。
圖2 是我國市場上主要啤酒的風味物質經主成分分析後的前兩個主成分的平面坐標。分析的風味成分有乙醛、乙酸乙酯、異丁酯、乙酸異戊酯、異戊醇及己酸乙酯。分析的時間跨度為半年, 這些數據通過主成分分析法後, 提取前兩個主成分, 這兩個主成分可以反映全部信息的83.1 %, 提取較為完全, 這說明這兩個主成分替代原始的6 個風味成分反映的樣品信息。百威啤酒、喜力啤酒和青島啤酒是我國啤酒市場上的3 種知名品牌,同時這3 種啤酒的質量也是得到人們的認可的。
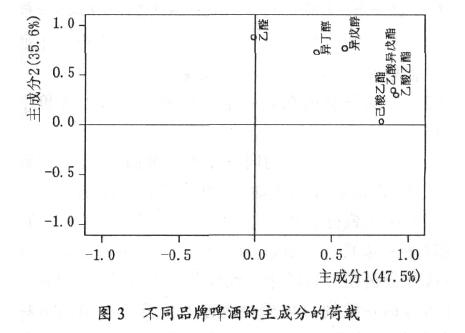
從圖2 可看出, 儘管百威啤酒、喜力啤酒和青島啤酒隨著時間的變化每種啤酒的風味成分的含量有所波動, 但是, 每種啤酒還是各自成一團, 自成一類, 三者的中心猶如一個三角形的3 個頂點, 三者組成一個風味三角形。從圖2 還可看出, 南方某品牌的啤酒有獨自成型的特點, 即其不同於青島啤酒、也不同喜力啤酒和百威啤酒的風格,實際上通過感官品嘗也可以得到此結論。主成分分析法採用的分類是可以通過對主成分的分析做出解釋的,圖3 是前兩個主成分的因數荷載圖。
從圖3 可以看出, 主成分 1 主要由乙酸乙酯、乙酸異戊酯和己酸乙酯決定, 這些酯含量高, 主成分1 就越大, 即主成分1 代表了啤酒的酯香, 酯香越濃, 主成分 1就越大。主成分2 主要由乙醛、異丁醇和異戊醇決定,這些成分能夠代表啤酒的“酒勁”的大小, 這些成分含量越高,主成分2 就越大,即啤酒的酒味就越重。結合這種解釋, 就可以對圖2 中的分類做出分析, 其中百威啤酒是酒味適中和酯香相對較濃的“濃香型”啤酒, 喜力啤酒是酒味和酯香均較濃的“濃醇型”啤酒, 青島啤酒是酒味較重, 而酯香較弱的“醇型”啤酒, 而某品牌的啤酒則是酒味和酯香均弱的“淡型”啤酒。
3.2 主成分分析法在同一品牌啤酒風味一致性評價中的應用
3.2.1 主成分分析法在同一品牌不同生產廠之間一致性評價中的應用
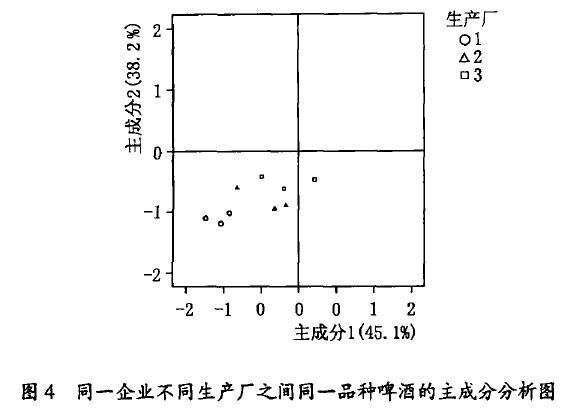
近十幾年來, 我國啤酒行業發展非常快, 啤酒企業的規模越來越大, 很多啤酒企業已經走出啤酒的“原產地”到異地建廠,進一步擴大企業的規模。對於一些啤酒企業來說, 新建廠面對的消費群體和建廠前面對的消費群體較為一致, 這時就要求新建廠生產的啤酒要與原廠生產的啤酒風格一致, 以免生產廠在切換時, 消費者不認可的情況發生。圖4 是同一企業的3 個不同生產廠之間的同一品種啤酒的主成分分析圖。
從圖4 可以看出, 總的來說, 3 個生產廠生產的啤酒還是比較一致的, 因為3 個廠生產的同一品種的啤酒的波動範圍較小。從圖4 還可以看出, 生產廠1 因為生產的歷史長, 生產較穩定, 因此其波動較小(圖中的圓圈);生產廠2 和生產廠3 的穩定性就稍差一點, 這是由於這兩個廠都是新廠,有個磨合的過程。同時,生產廠2
和生產廠1 的風味較為一致, 生產廠 3 和生產廠1 的一致性就稍差,其中生產廠3 是最新的廠。
3.2.2 主成分分析在同一生產廠啤酒一致性評價中的應用
同一生產廠生產的同一品種的啤酒, 由於不同時間的水質、原輔料等的波動, 最終體現在產品風味的波動上。同一主成分分析也可以評價產品隨時間的一致性。現以某一啤酒企業2006 年生產的某品種啤酒為例說明主成分分析在產品風味一致性評價中的應用。要評價啤酒風味的一致性, 啤酒企業首先要測定啤酒的風味指標,目前通過頂空-毛細管技術能測定大約10 種的風味物質,分別為乙醛、DMS、甲酸乙酯、乙酸乙酯、乙酸異丁酯、正丙醇、異丁醇、乙酸異戊酯、異戊醇和己酸乙酯。以前的一些統計技術例如統計過程式控制制(SPC)的控製圖等只能說明某一指標的波動情況, 而不能從總體上反映產品的波動性, 因為有些指標的波動, 不會引起產品風格的波動, 而主成分分析法, 是從總體上說明產品的波動性,比控製圖更能說明產品的波動性。
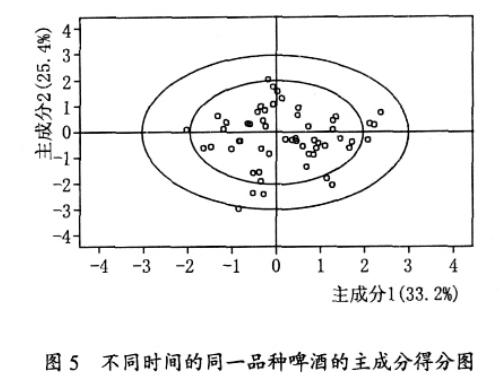
圖5 是某啤酒企業 2006 年一年生產的某品種的啤酒的10 種風味指標的前兩個主成分的平面坐標圖,這兩個主成分可反映產品約60 %的信息。圖 5 中的第一個小橢圓是95 %的置信區, 即在這個橢圓外的點占5 %, 通過對該橢圓外的點進行跟進分析可以發現波動的原因, 併在以後的生產過程中加以避免, 以提高產品的一致性。
4.1 主成分分析法, 可以消除各變數之間的共線性, 減少變數的個數,利於後續的分析。
4.2 使用主成分分析可以按照事物的相似性區分產品, 結果可用一維、二維或三維平面坐標圖標示, 特別直觀。
4.3 將樣品的數據通過主成分分析進行濃縮, 然後通過平面坐標可以實現從總體上對樣品進行一致性的分析,一般的統計技術只能對某一指標進行評價。
4.4 靜態頂空進樣高效毛細管氣相色譜分析啤酒香味組分技術結合, 主成分分析技術可以有效地應用於評價不同品牌啤酒風味的差異性、同一啤酒的風味一致性與均一性。
案例二:主成分分析法在食品領域的應用[1]
一、在食品風味方面的應用
目前,主成分分析應用還是比較廣泛的,但是就食品風味方面,關於該分析方法的文獻鮮見報道。戴素賢等人對七種高香型烏龍茶中的香氣成分進行了主成分分析,他們嘗試用主成分分析法來研究茶業香型的變化,併進而找到影響這些香型變化的主要化合物,同時還發現了不同的茶別中香氣化合物變化的趨勢併進行了模擬量化,直觀地表現了各種香氣化合物對香氣的貢獻程度。李華等運用多元統計分析確定葡萄酒感官特性,多元統計分析中的主成分分析等數學工具能夠把大量的描述葡萄酒感官特性的描述語精簡成較少的綜合性更強的描述語,這些精簡後的描述語不但能夠反映精簡前描述語的信息,還可以篩選出科學合理的描述符,描述符是描述分析的語言和應用主成分分析法完成了不同品牌啤酒風味差異性的評價,同一品牌啤酒風味一致性的評價,同一品牌不同生產廠之間一致性的評價以及同一生產廠啤酒一致性的評價這些工作。啤酒是個多指標的風味食品,主成分分析法可以幫助我們更好地研究啤酒理化指標和啤酒風格之間的相關性,從而達到更好地理解啤酒風味的目的。岳田利等人則通過利用主成分分析的方法建立了蘋果酒香氣質量的評價模型,並以此來對蘋果酒樣品香氣組分進行客觀的統計分析。S.Kallithraka等採用高效液相色譜法和氣相色譜法研究了希臘國內不同產地葡萄酒的化合物成分和感官特性,並運用了PCA法(主成分分析法)對所得參數進行多元分析,最終達到給葡萄酒評價和分類的目的。
二、在食品品質方面的應用
食品品質的評價往往是非常複雜的過程。因為影響食品品質的因素大量存在,非人為因素如食品環境中的微生物,溫度及pH等的變化帶來的影響。另一方面,由於人為的因素摻假也會造成食品品質的低劣,進而損害廣大銷售者和消費者的利益。如黎海紅等人運用主成分分析法對摻偽芝麻油的檢測方法進行研究分析。根據主成分分析的實驗原理,可以選擇芝麻油的折光率、酸價、色澤、水分及揮發物、皂化值和碘價等理化指標作為變數,將這些變數的所測數據做矩陣處理最後分析就能知道摻偽芝麻油的主成分及其貢獻率。我們知道,芝麻油摻雜了其他的植物油,其理化指標就會出現變化,這是質量鑒別的基礎和依據。利用主成分分析可以從大量的數據中提取與芝麻油摻偽相關的有用的信息,最終可以較好地區分摻雜有其他植物油的芝麻油。採用主成分分析方法還可以評價分析麵條的品質,麵條品質的感官評價存在著一定的缺陷,在麵條品質評價的過程中,需要對大量的待測樣本屬性進行測量,在這些屬性中有一些是由相互關聯的數據組成的,如麵條的韌性會影響麵條的拉斷力和平均拉力,因此,拉斷力和平均拉力是相關的,倘若在預測韌性的相應等式中同時用到了拉斷力和平均拉力,那麼預測出的韌性要比實際韌性大,因為進行了重覆計算,所以一定要確保等式中的變數之間儘可能地保持獨立,主成分分析在這樣的情況下通過對一組影響某一問題的相關變數進行線性變換,使得變換後得到的變數獨立不相關就叫做主成分,這樣的主成分不僅保留了原來相關變數中的主要信息,彼此間又不相關。麵條品質通過主成分分析法得到的綜合評價與主觀評價(外觀、色澤、適口性、咬勁、彈性、黏性、食味等)有相似之處,但是它比主觀評價更加細化,對具體樣本進行了量化,為麵條品質的進一步分析提供了可靠的參考依據。
主成分分析法還可以應用於保健食品功能學評價的研究,評價保健食品的功能特性—對抗疲勞和耐缺氧作用。利用主成分分析對包括受試小鼠外周血象和血清等23項生化指標進行綜合分析,科學合理地“降維”後,剋服了多指標綜合評價帶來的統計和分析,篩選出與抗疲勞和耐缺氧功效最直接相關的主要功效指標,依據主要考核變數的綜合評分最終確定受試樣品的功效特性大小。可見,主成分分析法可以作為一種方便、快捷和準確的量化評價功能學特性的新方法。
本条目由以下用户参与贡献
Angle Roh,funwmy,Zfj3000,Zhoujinsong-zjs,Dan,Beifu,Yixi,Tears~,twq,裴老师,Vulture,连晓雾,Mis铭,丁金鹏,y桑,Tracy,wzh.評論(共53條)
當維數大於時..就要使變數少於個,也就是維數小於.. 故意保留??
不是故意保留,是編輯遺漏,已更正,謝謝你的建議!
步驟4中,Z為p維,b也是p維,m指的是取m個主特征向量,這樣就可以得到m個主成分,每個主成分其實就是原向量與對應特征向量的內積
得出主成分如何與數據對上號?若有例題分析就好了,過程全懂,一到結果分析就暈
補充了個主成分分析法在啤酒風味評價分析中的應用 希望能用的上
第一次參與編輯,好像沒想像的難,哈
感謝Beifu的精彩貢獻
摟住您好!我現在正在用主成分分析方法,我不是這個專業的,只是自學了一點,我用他在SPSS處理後得到得數據怎麼才能知道原數據哪些屬於第一主成分,哪些屬於第二主成分呢?謝謝您啦!看了很多書也不懂哦
摟住您好!我現在正在用主成分分析方法,我不是這個專業的,只是自學了一點,我用他在SPSS處理後得到得數據怎麼才能知道原數據哪些屬於第一主成分,哪些屬於第二主成分呢?謝謝您啦!看了很多書也不懂哦
特征值按從大到小排,最大的是第一主成份,以此類推。
spss相關係數矩陣不正定對主成分分析影響?? 是否能用主成分分析法
是的,能用主城分析發的
spss給出的“成份矩陣”中,x7: 0.400 -0.235 0.343 -0.176 0.388 -0.269 其中,沒有大於0.5的,怎麼辦?另外,沒有最大的特征值負載在提取出來的最後一個主成分上,是那裡出問題了,請不吝賜教。
主分是不是就是坐標軸?用pca的目的是降維,得到一個新的矩陣,這個新的矩陣是主成分的得分矩陣。。。。這麼理解對嗎?(嘻嘻。。。我是初學者。。。謝啦)
摟住您好!我現在正在用主成分分析方法,我不是這個專業的,只是自學了一點,我用他在SPSS處理後得到得數據怎麼才能知道原數據哪些屬於第一主成分,哪些屬於第二主成分呢?謝謝您啦!看了很多書也不懂哦
你現在懂了嗎,我現在也正開始看,和你一樣的問題,幫我解釋一下可以嗎?
請問下主成分分析有哪些參考書?
你找參考書了嗎,幫我推薦一下,謝謝啦~
添加了新內容,希望對您有幫助!
你好,請教一下主成分分析法需要有數據才能分析麽?
?沒有數據能分析啥呢?









受益匪淺