信息量

出自 MBA智库百科(https://wiki.mbalib.com/)

信息量(Information Quantity)

　　信息量是源於通信領域而逐漸普及成為大眾與媒體頻繁使用的一個詞。假如你從未到過智庫百科，也沒有看過或聽過任何有關智庫百科的有關介紹，那麼智庫百科對你來說就是一個“未知數”，存在著所謂“不確定性”(uncertainty)。一旦你到過智庫百科，你就能瞭解到智庫百科的具體情況——“信息”。“信息”將幫你逐漸解開頭腦中的疑團，消除你對“智庫百科”認識上的不確定性，並由不確定性變成較為確定或確定。如獲得的“信息”越多，你對“智庫百科”的瞭解就越全面。當你到過智庫百科以後對它的瞭解越多，說明它的信息量就越大。

　　如何計算信息量的多少？在日常生活中，極少發生的事件一旦發生是容易引起人們關註的，而司空見慣的事不會引起註意，也就是說，極少見的事件所帶來的信息量多。如果用統計學的術語來描述，就是出現概率小的事件信息量多。因此，事件出現得概率越小，信息量愈大。即信息量的多少是與事件發生頻繁(即概率大小)成反比。

　　1.如已知事件Xi已發生，則表示Xi所含有或所提供的信息量

　　H(Xi) = − logaP(Xi)

　　例題：若估計在一次國際象棋比賽中謝軍獲得冠軍的可能性為0.1(記為事件A)，而在另一次國際象棋比賽中她得到冠軍的可能性為0.9(記為事件B)。試分別計算當你得知她獲得冠軍時，從這兩個事件中獲得的信息量各為多少？

　　　　　　H(A)=-log2 P(0.1)≈3.32(比特)

　　　　　　H(B)=-log2 P(0.9)≈0.152(比特)

　　2.統計信息量的計算公式為：

Xi —— 表示第i個狀態(總共有n種狀態)；

P(Xi)——表示第i個狀態出現的概率；

H(X)——表示用以消除這個事物的不確定性所需要的信息量。

　　例題：向空中投擲硬幣，落地後有兩種可能的狀態，一個是正面朝上，另一個是反面朝上，每個狀態出現的概率為1/2。如投擲均勻的正六面體的骰子，則可能會出現的狀態有6個，每一個狀態出現的概率均為1/6。試通過計算來比較狀態的不肯定性與硬幣狀態的不肯定性的大小。

H(硬幣)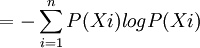

= -(2×1/2)×logP2(1/2)≈1(比特)

H(骰子)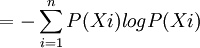

= -6×(1/6)×logP2(1/6)≈2.6(比特)

　　由以上計算可以得出兩個推論：

　　[推論1] 當且僅當某個P(Xi)=1，其餘的都等於0時， H(X)= 0。

　　[推論2]當且僅當某個P(Xi)=1/n，i=1， 2，……， n時，H(X)有極大值log n。