信息量

出自 MBA智库百科(https://wiki.mbalib.com/)

信息量(Information Quantity)

　　信息量是源于通信领域而逐渐普及成为大众与媒体频繁使用的一个词。假如你从未到过智库百科，也没有看过或听过任何有关智库百科的有关介绍，那么智库百科对你来说就是一个“未知数”，存在着所谓“不确定性”(uncertainty)。一旦你到过智库百科，你就能了解到智库百科的具体情况——“信息”。“信息”将帮你逐渐解开头脑中的疑团，消除你对“智库百科”认识上的不确定性，并由不确定性变成较为确定或确定。如获得的“信息”越多，你对“智库百科”的了解就越全面。当你到过智库百科以后对它的了解越多，说明它的信息量就越大。

　　如何计算信息量的多少？在日常生活中，极少发生的事件一旦发生是容易引起人们关注的，而司空见惯的事不会引起注意，也就是说，极少见的事件所带来的信息量多。如果用统计学的术语来描述，就是出现概率小的事件信息量多。因此，事件出现得概率越小，信息量愈大。即信息量的多少是与事件发生频繁(即概率大小)成反比。

　　1.如已知事件Xi已发生，则表示Xi所含有或所提供的信息量

　　H(Xi) = − logaP(Xi)

　　例题：若估计在一次国际象棋比赛中谢军获得冠军的可能性为0.1(记为事件A)，而在另一次国际象棋比赛中她得到冠军的可能性为0.9(记为事件B)。试分别计算当你得知她获得冠军时，从这两个事件中获得的信息量各为多少？

　　　　　　H(A)=-log2 P(0.1)≈3.32(比特)

　　　　　　H(B)=-log2 P(0.9)≈0.152(比特)

　　2.统计信息量的计算公式为：

Xi —— 表示第i个状态(总共有n种状态)；

P(Xi)——表示第i个状态出现的概率；

H(X)——表示用以消除这个事物的不确定性所需要的信息量。

　　例题：向空中投掷硬币，落地后有两种可能的状态，一个是正面朝上，另一个是反面朝上，每个状态出现的概率为1/2。如投掷均匀的正六面体的骰子，则可能会出现的状态有6个，每一个状态出现的概率均为1/6。试通过计算来比较状态的不肯定性与硬币状态的不肯定性的大小。

H(硬币)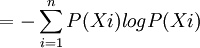

= -(2×1/2)×logP2(1/2)≈1(比特)

H(骰子)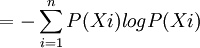

= -6×(1/6)×logP2(1/6)≈2.6(比特)

　　由以上计算可以得出两个推论：

　　[推论1] 当且仅当某个P(Xi)=1，其余的都等于0时， H(X)= 0。

　　[推论2]当且仅当某个P(Xi)=1/n，i=1， 2，……， n时，H(X)有极大值log n。