判別分析
出自 MBA智库百科(https://wiki.mbalib.com/)
判別分析(discriminant analysis)
目錄 |
判別分析又稱為線性判別分析（Linear Discriminant Analysis）產生於20世紀30年代，是利用已知類別的樣本建立判別模型，為未知類別的樣本判別的一種統計方法。近年來，判別分析在自然科學、社會學及經濟管理學科中都有廣泛的應用。判別分析的特點是根據已掌握的、歷史上每個類別的若幹樣本的數據信息，總結出客觀事物分類的規律性，建立判別公式和判別準則。當遇到新的樣本點時，只要根據總結出來的判別公式和判別準則，就能判別該樣本點所屬的類別。判別分析按照判別的組數來區分，可以分為兩組判別分析和多組判別分析。
判別分析(Discriminatory Analysis)的任務是根據已掌握的１批分類明確的樣品，建立較好的判別函數，使產生錯判的事例最少，進而對給定的1個新樣品，判斷它來自哪個總體。
根據資料的性質，分為定性資料的判別分析和定量資料的判別分析；採用不同的判別準則，又有費歇、貝葉斯、距離等判別方法。
費歇（FISHER）判別思想是投影，使多維問題簡化為一維問題來處理。選擇一個適當的投影軸,使所有的樣品點都投影到這個軸上得到一個投影值。對這個投影軸的方向的要求是：使每一類內的投影值所形成的類內離差儘可能小，而不同類間的投影值所形成的類間離差儘可能大。
貝葉斯（BAYES）判別思想是根據先驗概率求出後驗概率，並依據後驗概率分佈作出統計推斷。所謂先驗概率,就是用概率來描述人們事先對所研究的對象的認識的程度；所謂後驗概率，就是根據具體資料、先驗概率、特定的判別規則所計算出來的概率。它是對先驗概率修正後的結果。
距離判別思想是根據各樣品與各母體之間的距離遠近作出判別。即根據資料建立關於各母體的距離判別函數式，將各樣品數據逐一代入計算，得出各樣品與各母體之間的距離值，判樣品屬於距離值最小的那個母體。
判別分析的方法有參數方法和非參數方法。參數方法假定每個類的觀測來自（多元）正態分佈總體，各類的分佈的均值（中心）可以不同。非參數方法不要求知道各類所來自總體的分佈，它對每一類使用非參數方法估計該類的分佈密度，然後據此建立判別規則。
記X為用來建立判別規則的P維隨機變數，S為合併協方差陣估計，t=1,...,G為組的下標，共有G個組。記nt為第t組中訓練樣本的個數，m_t為第t組的自變數均值向量，St為第t組的協方差陣， | St | 為St的行列式，qt為第t組出現的先驗概率，p(t|x)為自變數為x的觀測屬於第t組的後驗概率，ft(x)為第t組的分佈密度在X=x處的值，f(x)為非條件密度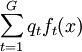
。
按照Bayes理論，自變數為x的觀測屬於第t組的後驗概率p(t | x) = qtft(x) / f(x)。於是，可以把自變數X的取值空間R^P劃分為G個區域Rt,t=1,...,G，使得當X的取值x屬於R_t時後驗概率在第t組最大，即
建立的判別規則為：計算自變數x到每一個組中心的廣義平方距離，並把x判入最近的類。廣義平方距離的計算可能使用合併的協方差陣估計或者單獨的協方差陣估計，並與先驗概率有關，定義為
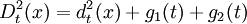
其中
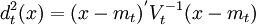
Vt = St （使用單個類的協方差陣估計）或 Vt = S（使用合併的協方差陣估計）。mt可以用第t組的均值\overline{X_t}代替。在使用合併協方差陣時，
其中x'S − 1x是共同的可以不考慮，於是在比較x到各組中心的廣義平方距離時，只要計算線性判別函數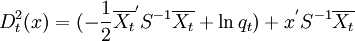
，當x到第t組的線性判別函數最大時把x對應觀測判入第t組。在如果使用單個類的協方差陣估計Vt = St則距離函數是x的二次函數，稱為二次判別函數。
後驗概率可以用廣義距離表示為
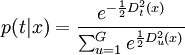
因此，參數方法的判別規則為：先決定是使用合併協方差陣還是單個類的協方差陣，計算x到各組的廣義距離，把x判入最近的組；或者計算x屬於各組的後驗概率，把x判入後驗概率最大的組。如果x的最大的後驗概率都很小（小於一個給定的界限），則把它判入其它組。
非參數判別方法仍使用Bayes後驗概率密度的大小來進行判別，但這時第t組在x處的密度值ft(x)不再具有參數形式，不象參數方法那樣可以用mt和St（或St）表示出來。非參數方法用核方法或最近鄰方法來估計概率密度ft(x)。
最近鄰估計和核估計也都需要定義空間中的距離。除了可以用歐氏距離外，還可以用馬氏（Mahalanobis）距離，定義為：
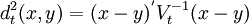
其中Vt為以下形式之一：
Vt = S合併協方差陣
Vt = diag(S)合併協方差陣的對角陣
Vt = St第t組內的協方差陣
Vt = diag(St)第t組內的協方差陣的對角陣
Vt = I單位陣，這時距離即普通歐氏距離
