全球专业中文经管百科，由121,994位网友共同编写而成，共计436,017个条目

查看

工具▼

歐氏距離

用手机看条目

出自 MBA智库百科(https://wiki.mbalib.com/)

歐氏距離（Euclidean Distance）

目錄

1 什麼是歐氏距離
2 歐氏距離的計算公式
3 歐氏距離變換
4 閔氏距離
5 相關條目

什麼是歐氏距離

　　歐氏距離也稱歐幾裡得距離或歐幾裡得度量，是一個通常採用的距離定義，它是在m維空間中兩個點之間的真實距離。在二維和三維空間中的歐氏距離的就是兩點之間的距離。使用這個距離，歐氏空間成為度量空間。相關聯的範數稱為歐幾裡得範數。較早的文獻稱之為畢達哥拉斯度量。

歐氏距離的計算公式

二維空間的公式

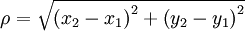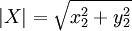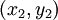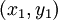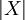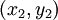　　 $\rho=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}$ ， $\left|X\right|=\sqrt{x_2^2+y_2^2}$ 。其中， $ρ$ 為點 $\left(x_2,y_2\right)$ 與點 $\left(x_1,y_1\right)$ 之間的歐氏距離； $\left|X\right|$ 為點 $\left(x_2,y_2\right)$ 到原點的歐氏距離。　　

三維空間的公式

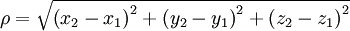
　　 $\rho=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2+\left(z_2-z_1\right)^2}$

　　 $\left|X\right|=\sqrt{x_2^2+y_2^2+z_2^2}$ 　　

n維空間的公式

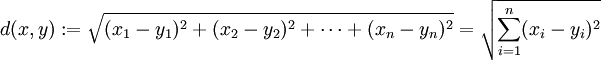
　　 $d(x,y):=\sqrt{(x_1-y_1)^2+(x_2-y_2)^2+\cdots+(x_n-y_n)^2}=\sqrt{\sum_{i=1}^n(x_i-y_i)^2}$ 　　

歐氏距離變換

　　所謂歐氏距離變換，是指對於一張二值圖像（在此我們假定白色為前景色，黑色為背景色），將前景中的像素的值轉化為該點到達最近的背景點的距離。

　　歐氏距離變換在數字圖像處理中的應用範圍很廣泛，尤其對於圖像的骨架提取，是一個很好的參照。　　

閔氏距離

　　閔氏距離又叫做閔可夫斯基距離,是歐氏空間中的一種測度，被看做是歐氏距離的一種推廣，歐氏距離是閔可夫斯基距離的一種特殊情況。

　　定義式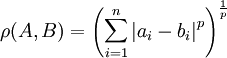： $\rho(A,B)=\left ( {\sum_{i=1}^n \left | {a_i-b_i} \right |^p } \right )^{\frac{1}{p}}$

　　閔可夫斯基距離公式中，當p=2時，即為歐氏距離；當p=1時，即為曼哈頓距離；當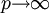 $p{\rightarrow}\infty$ 時，即為切比雪夫距離。

相關條目

曼哈頓距離

取自"https://wiki.mbalib.com/zh-tw/%E6%AC%A7%E6%B0%8F%E8%B7%9D%E7%A6%BB"

打开MBA智库App, 阅读完整内容打开App

如果您認為本條目還有待完善，需要補充新內容或修改錯誤內容，請編輯條目或投訴舉報。

本条目由以下用户参与贡献

otf125,nonameh.

頁面分類: 應用數學

評論(共0條)

提示:評論內容為網友針對條目"歐氏距離"展開的討論，與本站觀點立場無關。

發表評論請文明上網，理性發言並遵守有關規定。

以上内容根据网友推荐自动排序生成

闽公网安备 35020302032707号