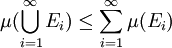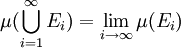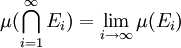測度
出自 MBA智库百科(https://wiki.mbalib.com/)
測度(Measure)
目錄 |
數學上,測度(Measure)是一個函數,它對一個給定集合的某些子集指定一個數,這個數可以比作大小、體積、概率等等。傳統的積分是在區間上進行的,後來人們希望把積分推廣到任意的集合上,就發展出測度的概念,它在數學分析和概率論有重要的地位。
測度論是實分析的一個分支,研究對象有σ代數、測度、可測函數和積分,其重要性在概率論和統計學中有所體現的。
形式上說,一個測度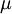 (詳細的說法是可列可加的正測度)是個函數。設
(詳細的說法是可列可加的正測度)是個函數。設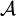 是集合
是集合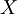 上的一個σ代數,
上的一個σ代數,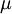 在上
在上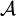 定義,於擴充區間
定義,於擴充區間![[0,\infty]](/w/images/math/3/1/5/315e0047ccbfa87354192dac2fe986fb.png) 中取值,並且滿足以下性質:
中取值,並且滿足以下性質:
- 空集的測度為零:
-
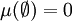 。
。
-
- 可數可加性,或稱σ可加性:若
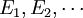 為
為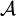 中可數個兩兩不交的集合的序列,則所有
中可數個兩兩不交的集合的序列,則所有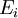 的並集的測度,等於每個
的並集的測度,等於每個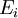 的測度之總和:
的測度之總和:
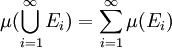 。
。
這樣的三元組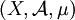 稱為一個測度空間,而
稱為一個測度空間,而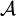 中的元素稱為這個空間中的可測集。
中的元素稱為這個空間中的可測集。
下麵的一些性質可從測度的定義導出:
測度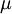 的單調性:
的單調性:
若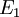 和
和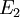 為可測集,而且
為可測集,而且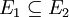 ,則
,則 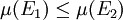 。
。
若 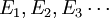 為可測集(不必是兩兩不交的),並且對於所有的
為可測集(不必是兩兩不交的),並且對於所有的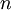 ,
, ⊆
⊆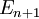 ,則集合
,則集合 的並集是可測的,且有如下不等式(「次可列可加性」):
的並集是可測的,且有如下不等式(「次可列可加性」):
以及如下極限:
若 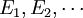 為可測集,並且對於所有的
為可測集,並且對於所有的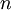 ,
,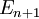 ⊆
⊆ ,則
,則 的交集是可測的。進一步說,如果至少一個
的交集是可測的。進一步說,如果至少一個 的測度有限,則有極限:
的測度有限,則有極限:
如若不假設至少一個 的測度有限,則上述性質一般不成立。例如對於每一個
的測度有限,則上述性質一般不成立。例如對於每一個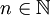 ,令
,令
這裡,全部集合都具有無限測度,但它們的交集是空集。
如果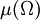 是一個有限實數(而不是
是一個有限實數(而不是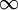 ),則測度空間
),則測度空間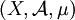 稱為有限測度空間。如果
稱為有限測度空間。如果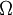 可以表示為可數個可測集的並集,而且這些可測集的測度均有限,則該測度空間稱為σ有限測度空間。稱測度空間中的一個集合
可以表示為可數個可測集的並集,而且這些可測集的測度均有限,則該測度空間稱為σ有限測度空間。稱測度空間中的一個集合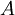 具有σ有限測度,如果
具有σ有限測度,如果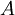 可以表示為可數個可測集的並集,而且這些可測集的測度均有限。
可以表示為可數個可測集的並集,而且這些可測集的測度均有限。
作為例子,實數集賦以標準勒貝格測度是σ有限的,但不是有限的。為說明之,只要考慮閉區間族[k, k+1],k 取遍所有的整數;這樣的區間共有可數多個,每一個的測度為1,而且並起來就是整個實數集。作為另一個例子,取實數集上的計數測度,即對實數集的每個有限子集,都把元素個數作為它的測度,至於無限子集的測度則令為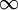 。這樣的測度空間就不是σ有限的,因為任何有限測度集只含有有限個點,從而,覆蓋整個實數軸需要不可數個有限測度集。σ有限的測度空間有些很好的性質;從這點上說,σ有限性可以類比於拓撲空間的可分性。
。這樣的測度空間就不是σ有限的,因為任何有限測度集只含有有限個點,從而,覆蓋整個實數軸需要不可數個有限測度集。σ有限的測度空間有些很好的性質;從這點上說,σ有限性可以類比於拓撲空間的可分性。
一個可測集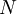 稱為零測集,如果
稱為零測集,如果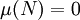 。零測集的子集稱為可去集,它未必是可測的,但零測集自然是可去集。如果所有的可去集都可測,則稱該測度為完備測度。
。零測集的子集稱為可去集,它未必是可測的,但零測集自然是可去集。如果所有的可去集都可測,則稱該測度為完備測度。
一個測度可以按如下的方式延拓為完備測度:考慮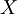 的所有這樣的子集
的所有這樣的子集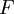 ,它與某個可測集
,它與某個可測集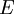 僅差一個可去集,也就是說
僅差一個可去集,也就是說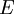 與
與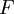 的對稱差包含於一個零測集中。由這些子集
的對稱差包含於一個零測集中。由這些子集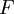 生成的σ代數,並定義
生成的σ代數,並定義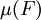 的值就等於
的值就等於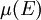 。
。
下列是一些測度的例子(重要性與順序無關)。
- 計數測度 定義為
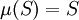 的‘元素個數’。
的‘元素個數’。
- 一維勒貝格測度 是定義在
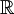 的一個含所有區間的σ代數上的、完備的、平移不變的、滿足
的一個含所有區間的σ代數上的、完備的、平移不變的、滿足![\mu([0,1])=1\](/w/images/math/c/7/a/c7a36793073e1288383b0d6b7690dea7.png) 的唯一測度。
的唯一測度。
- Circular angle 測度 是旋轉不變的。
- 局部緊拓撲群上的哈爾測度是勒貝格測度的一種推廣,而且也有類似的刻劃。
- 恆零測度 定義為
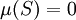 ,對任意的
,對任意的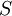 。
。
- 每一個概率空間都有一個測度,它對全空間取值為1(於是其值全部落到單位區間[0,1]中)。這就是所謂概率測度。
- 其它例子,包括:狄拉克測度、波萊爾測度、若爾當測度、遍歷測度、歐拉測度、高斯測度、貝爾測度、拉東測度。