因數分析法
出自 MBA智库百科(https://wiki.mbalib.com/)
因數分析法(Factor Analysis Method)
目錄 |
因數分析法是指從研究指標相關矩陣內部的依賴關係出發，把一些信息重疊、具有錯綜複雜關係的變數歸結為少數幾個不相關的綜合因數的一種多元統計分析方法。基本思想是：根據相關性大小把變數分組，使得同組內的變數之間相關性較高，但不同組的變數不相關或相關性較低，每組變數代表一個基本結構一即公共因數。
應用因數分析法的主要步驟如下：
(1)對數據樣本進行標準化處理。
(2)計算樣本的相關矩陣R。
(3)求相關矩陣R的特征根和特征向量。
(4)根據系統要求的累積貢獻率確定主因數的個數。
(5)計算因數載荷矩陣A。
(6)確定因數模型。
(7)根據上述計算結果，對系統進行分析。
因數分析法的實例 [1]
【例：1】
假設某一社會經濟系統問題，其主要特性可用4個指標表示，它們分別是生產、 技術、交通和環境。其相關矩陣為：
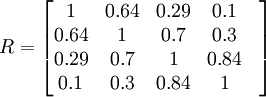
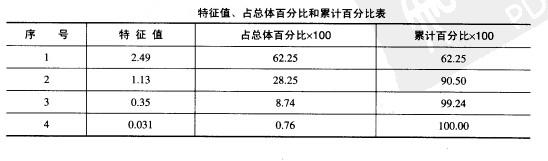
相應的特征值、占總體百分比和累計百分比如下表：
對應特征值的特征向量矩陣為：
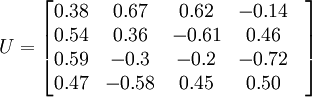
假如要求所取特征值反映的信息量占總體信息量的90％以上，則從累計特征值所占百分 比看，只需取前兩項即可。也就是說，只需取兩個主要因數。對應於前兩列特征值的特征向量，
可求得其因數載荷矩陣A為：
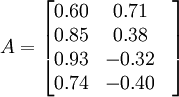
於是，該問題的因數模型為：
Xl = 0.60f1 + 0.71f2
X2 = 0.85f1 + 0.38f2
X3 = 0.93f1 − 0.32f2
X4 = 0.74f1 − 0.40f2
由以上可以看出，兩個因數中，f1是全面反映生產、技術、交通和環境的因數，而f2卻不同，它反映了對生產和技術這兩項增長有利，而對交通和環境增長不利的因數。也就是說，按照原有統計資料得出的相關矩陣分析的結果是如果生產和技術都隨f2增長了，將有可能出現交通緊張和環境惡化的問題，f2反映了這兩方面的相互制約狀況。
因數分析與主成分分析的區別 [2]
因數分析法與主成分分析法都屬於因素分析法，都基於統計分析方法，但兩者有較大的區別：主成分分析是通過坐標變換提取主成分，也就是將一組具有相關性的變數變換為一組獨立的變數，將主成分表示為原始觀察變數的線性組合；而因數分析法是要構造因數模型，將原始觀察變數分解為因數的線性組合。通過對上述內容的學習，可以看出因數分析法和主成分分析法的主要區別為：
(1)主成分分析是將主要成分表示為原始觀察變數的線性組合，而因數分析是將原始觀察變數表示為新因數的線性組合，原始觀察變數在兩種情況下所處的位置不同。
(2)主成分分析中，新變數Z的坐標維數j(或主成分的維數)與原始變數維數相同，它只是將一組具有相關性的變數通過正交變換轉換成一組維數相同的獨立變數，再按總方差誤差的允許值大小，來選定q個(q<p)主成分；而因數分析法是要構造一個模型，將問題的為數眾多的變數減少為幾個新因數，新因數變數數m小於原始變數數P，從而構造成一個結構簡單的模型。可以認為，因數分析法是主成分分析法的發展。
(3)主成分分析中，經正交變換的變數繫數是相關矩陣R的特征向量的相應元素；而因數分析模型的變數繫數取自因數負荷量，即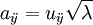
。因數負荷量矩陣A與相關矩陣R滿足以下關係：
其中，U為R的特征向量。
在考慮有殘餘項ε時，可設包含εi的矩陣ρ為誤差項，則有R − AAT = ρ。
在因數分析中，殘餘項應只在ρ的對角元素項中，因特殊項只屬於原變數項，因此，
的選擇應以ρ的非對角元素的方差最小為原則。而在主成分分析中，選擇原則是使捨棄成分所對應的方差項累積值不超過規定值，或者說被捨棄項各對角要素的自乘和為最小，這兩者是不同的。
太繞了，小弟沒理解，如果有使用場景，就更好了