全球专业中文经管百科，由121,994位网友共同编写而成，共计436,015个条目

相關矩陣

用手机看条目

出自 MBA智库百科(https://wiki.mbalib.com/)

相關矩陣(Correlation Matrix)

目錄

[編輯]

相關矩陣概述[1]

　　P個相關變數，求兩變數之間的相關係數，共可得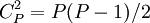C_P^2=P(P-1)/2個相關係數。如按變數的編號順序，依次將它們排列成一數字方陣，此方陣就稱為相關矩陣。常用字母R表示。

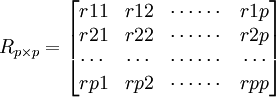
R_{p\times p}=\begin{bmatrix} r11 & r12 & \cdots \cdots & r1p \\ r21 & r22 & \cdots \cdots & r2p \\ \cdots & \cdots & \cdots \cdots & \cdots \\ rp1 & rp2 & \cdots \cdots & rpp \end{bmatrix}

　　從左上到右下方向的對角線上，均是兩個相同變數的相關，其數值均是1，對角線以上部分的相關係數與以下部分的相關係數是對稱的。

[編輯]

幾種常見的組內相關矩陣[2]

　　下麵介紹幾種常見的組內相關矩陣結構。以重覆測量資料為例，常見的有等相關、相鄰相關、自相關、非確定相關等。其中最常用的是等相關與自相關。

　　1．等相關最簡單的組內相關是等相關，又稱為可交換的(exchangeable)，或復對稱的(compound symmetry)。即：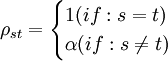
\rho_{st}=\begin{cases} 1(if:s=t) \\ \alpha (if:s\ne t) \end{cases}
　　以5次重覆測量為例，等相關的組內相關結構為：
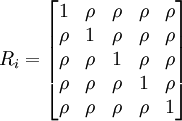
R_i=\begin{bmatrix} 1 & \rho & \rho & \rho & \rho \\ \rho & 1 & \rho & \rho & \rho \\ \rho & \rho & 1 & \rho & \rho \\ \rho & \rho & \rho & 1 & \rho \\ \rho & \rho & \rho & \rho & 1 \end{bmatrix}

　　2．相鄰相關相鄰相關即只有相鄰的重覆觀察值之間是相關的，否則不相關。1階相鄰相關是指相鄰的兩次觀察值間有相關。當各相鄰相關係數都相等時，這種相關稱為1階平穩的(stationary 1-de-pendence)，否則稱為1階非平穩的(nonstationary 1-dependence)。

　　以5次重覆測量為例，1階平穩和非平穩相鄰相關的組內相關結構分別為：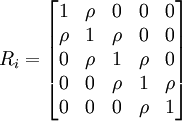
R_i=\begin{bmatrix} 1 & \rho & 0 & 0 & 0 \\ \rho & 1 & \rho & 0 & 0 \\ 0 & \rho & 1 & \rho & 0 \\ 0 & 0 & \rho & 1 & \rho \\ 0 & 0 & 0 & \rho & 1 \end{bmatrix},R_i=\begin{bmatrix} 1 & \rho_1 & 0 & 0 & 0 \\ \rho_1 & 1 & \rho_2 & 0 & 0 \\ 0 & \rho_2 & 1 & \rho_3 & 0 \\ 0 & 0 & \rho_3 & 1 & \rho_4 \\ 0 & 0 & 0 & \rho_4 & 1 \end{bmatrix}
　　2階平穩相鄰相關的組內相關結構分別為：
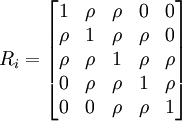
R_i=\begin{bmatrix} 1 & \rho & \rho & 0 & 0 \\ \rho & 1 & \rho & \rho & 0 \\ \rho & \rho & 1 & \rho & \rho \\ 0 & \rho & \rho & 1 & \rho \\ 0 & 0 & \rho & \rho & 1 \end{bmatrix}

　　不難推廣到k階相鄰相關的情形。顯然，平穩相關是非平穩相關的特例，等相關是平穩相關(當然也是非平穩相關)的特例。

　　3．自相關(autocorrelation)即相關與間隔次數有關，相鄰的兩次觀察值間相關為ρ，相隔次數越長，相關關係越小，以5次重覆測量為例，其組內相關結構為：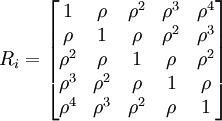
R_i=\begin{bmatrix} 1 & \rho & \rho^2 & \rho^3 & \rho^4 \\ \rho & 1 & \rho & \rho^2 & \rho^3 \\ \rho^2 & \rho & 1 & \rho & \rho^2 \\ \rho^3 & \rho^2 & \rho & 1 & \rho \\ \rho^4 & \rho^3 & \rho^2 & \rho & 1 \end{bmatrix}
　　這種相關稱為1階自相關(first order autocorrelation)。或更廣義地，兩次觀察值間的相關與觀察時間間隔有關：
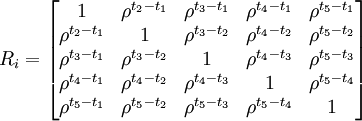
R_i=\begin{bmatrix} 1 & \rho^{t_2-t_1} & \rho^{t_3-t_1} & \rho^{t_4-t_1} & \rho^{t_5-t_1} \\ \rho^{t_2-t_1} & 1 & \rho^{t_3-t_2} & \rho^{t_4-t_2} & \rho^{t_5-t_2} \\ \rho^{t_3-t_1} & \rho^{t_3-t_2} & 1 & \rho^{t_4-t_3} & \rho^{t_5-t_3} \\ \rho^{t_4-t_1} & \rho^{t_4-t_2} & \rho^{t_4-t_3} & 1 & \rho^{t_5-t_4} \\ \rho^{t_5-t_1} & \rho^{t_5-t_2} & \rho^{t_5-t_3} & \rho^{t_5-t_4} & 1 \end{bmatrix}

　　4．非確定相關(unstructured，general structure)即相關矩陣的非對角線上的元素均不等。

　　5．獨立(independent，zero correlation)即塊矩陣A的非對角線上的元素均為0。

　　雖然組內相關矩陣結構的選擇可藉助於統計學方法進行判斷，但對具體資料，筆者建議按專業知識來確定其結構。

[編輯]

相關矩陣分析法[3]

　　相關矩陣分析法是20世紀70年代初，聯合國教科文組織在各國專家的協助下，建立和發展起來的一套確定科技優先發展領域的系統性方法。其核心就是在技術專家協助下，編製和分析D／D矩陣(發展目標之間的相關矩陣)、S／D矩陣(學科領域與發展目標的相關矩陣)和S／S矩陣(學科領域之間的相關矩陣)，該方法運用的關鍵是：①確定好問題的邊界(發展目標和科技領域條目劃分)；②設計好專家調查表(科學、合理、簡便)，選擇好咨詢專家；③做好三個相關矩陣的構造和系統分析。

[編輯]

相關矩陣的案例分析

[編輯]

案例一：[4]

　　通過考查相關矩陣來研究廣告費、銷售量和每加侖價格之間的關係。相關矩陣通過計算各對變數相互間的簡單相關係數來構造。

　　相關矩陣實例如表1所示。代表變數1和變數2之間關係的相關係數表示為r12。註意，第一個下標1指在表格中所在的行，第二個下標2指在表格中所在的列。這一方法使人一眼就能確定任何兩個變數之間的關係。當然，變數1和變數2之間的相關性與變數2和變數1之間的相關性相同，即r12 = r21。因此，只需要1／2的相關矩陣。此外，一個變數與它本身的相關性總是等於1，例如r11 = r22 = r33 = 1。

　　用電腦運行數據，所得到的相關矩陣如表2所示。對廣告費、銷售量和每加侖價格之間關係的調查顯示，新的自變數有助於改進預測結果。相關矩陣顯示，廣告費與因變數(銷售量)有很高的正相關性(r13 = 0.89)，與自變數(每加侖價格)有比較適度的負相關性(r23 = − 0.65)。這一相互關係的組合可以由廣告費來解釋一些不能被每加侖價格解釋的銷售量的總方差。我們將會看到，當同時使用每加侖價格和廣告費來估算銷售量時，R2增加到了93．2％。

　　相關矩陣的分析對涉及多個自變數問題的解決是重要的開始步驟。

表1 相關矩陣

變數
變數123
1r11r12r13
2r21r22r23
3r31r32r33

表2 數據的相關矩陣

變數
變數銷售額
1		價格
2		廣告費
3
銷售額11.00-0.860.89
價格21.00-0.65
廣告費31.00
[編輯]

相關條目

[編輯]

參考文獻

  1. ↑ 車文博主編.當代西方心理學新詞典.吉林人民出版社,2001年10月第1版.
  2. ↑ 饒克勤主編.第五章 廣義估計方程和多水平模型 衛生統計方法與應用進展第二捲.人民衛生出版社,2008.1.
  3. ↑ 吳樂山,孫建中主編 第五章 軍事醫學科學技術選擇和評估 現代軍事醫學戰略研究.軍事醫學科學出版社,2004年08月第1版.
  4. ↑ (美)約翰·E.漢克 迪恩·W.威切恩著 胡曉鳳譯.第七章 多元回歸分析 管理學系列 商業預測（第八版）.清華大學出版社,2006年07月第1版.
取自"https://wiki.mbalib.com/zh-tw/%E7%9B%B8%E5%85%B3%E7%9F%A9%E9%98%B5"
打开MBA智库App, 阅读完整内容 打开App
本條目對我有幫助20
赏
MBA智库APP

扫一扫，下载MBA智库APP

分享到：
  如果您認為本條目還有待完善，需要補充新內容或修改錯誤內容，請編輯條目或投訴舉報。

本条目由以下用户参与贡献

李漠,连晓雾.

評論(共0條)

提示:評論內容為網友針對條目"相關矩陣"展開的討論，與本站觀點立場無關。

發表評論請文明上網，理性發言並遵守有關規定。

百科VIP
百科VIP会员权益

  • 无广告阅读

  • 免验证复制

开通/续费百科VIP

消息

昵称未设置
百科VIP

未开通

收藏夹

账号安全中心

我的页面

我的贡献

我的讨论页

我的设置
退出登录
打开APP

以上内容根据网友推荐自动排序生成

下载APP

闽公网安备 35020302032707号