全球专业中文经管百科，由121,994位网友共同编写而成，共计435,843个条目

相关矩阵

用手机看条目

出自 MBA智库百科(https://wiki.mbalib.com/)

相关矩阵(Correlation Matrix)

目录

[编辑]

相关矩阵概述[1]

　　P个相关变量，求两变量之间的相关系数，共可得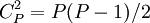C_P^2=P(P-1)/2个相关系数。如按变量的编号顺序，依次将它们排列成一数字方阵，此方阵就称为相关矩阵。常用字母R表示。

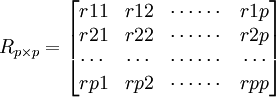
R_{p\times p}=\begin{bmatrix} r11 & r12 & \cdots \cdots & r1p \\ r21 & r22 & \cdots \cdots & r2p \\ \cdots & \cdots & \cdots \cdots & \cdots \\ rp1 & rp2 & \cdots \cdots & rpp \end{bmatrix}

　　从左上到右下方向的对角线上，均是两个相同变量的相关，其数值均是1，对角线以上部分的相关系数与以下部分的相关系数是对称的。

[编辑]

几种常见的组内相关矩阵[2]

　　下面介绍几种常见的组内相关矩阵结构。以重复测量资料为例，常见的有等相关、相邻相关、自相关、非确定相关等。其中最常用的是等相关与自相关。

　　1．等相关最简单的组内相关是等相关，又称为可交换的(exchangeable)，或复对称的(compound symmetry)。即：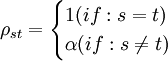
\rho_{st}=\begin{cases} 1(if:s=t) \\ \alpha (if:s\ne t) \end{cases}
　　以5次重复测量为例，等相关的组内相关结构为：
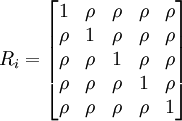
R_i=\begin{bmatrix} 1 & \rho & \rho & \rho & \rho \\ \rho & 1 & \rho & \rho & \rho \\ \rho & \rho & 1 & \rho & \rho \\ \rho & \rho & \rho & 1 & \rho \\ \rho & \rho & \rho & \rho & 1 \end{bmatrix}

　　2．相邻相关相邻相关即只有相邻的重复观察值之间是相关的，否则不相关。1阶相邻相关是指相邻的两次观察值间有相关。当各相邻相关系数都相等时，这种相关称为1阶平稳的(stationary 1-de-pendence)，否则称为1阶非平稳的(nonstationary 1-dependence)。

　　以5次重复测量为例，1阶平稳和非平稳相邻相关的组内相关结构分别为：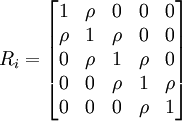
R_i=\begin{bmatrix} 1 & \rho & 0 & 0 & 0 \\ \rho & 1 & \rho & 0 & 0 \\ 0 & \rho & 1 & \rho & 0 \\ 0 & 0 & \rho & 1 & \rho \\ 0 & 0 & 0 & \rho & 1 \end{bmatrix},R_i=\begin{bmatrix} 1 & \rho_1 & 0 & 0 & 0 \\ \rho_1 & 1 & \rho_2 & 0 & 0 \\ 0 & \rho_2 & 1 & \rho_3 & 0 \\ 0 & 0 & \rho_3 & 1 & \rho_4 \\ 0 & 0 & 0 & \rho_4 & 1 \end{bmatrix}
　　2阶平稳相邻相关的组内相关结构分别为：
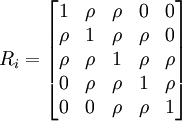
R_i=\begin{bmatrix} 1 & \rho & \rho & 0 & 0 \\ \rho & 1 & \rho & \rho & 0 \\ \rho & \rho & 1 & \rho & \rho \\ 0 & \rho & \rho & 1 & \rho \\ 0 & 0 & \rho & \rho & 1 \end{bmatrix}

　　不难推广到k阶相邻相关的情形。显然，平稳相关是非平稳相关的特例，等相关是平稳相关(当然也是非平稳相关)的特例。

　　3．自相关(autocorrelation)即相关与间隔次数有关，相邻的两次观察值间相关为ρ，相隔次数越长，相关关系越小，以5次重复测量为例，其组内相关结构为：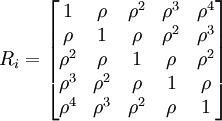
R_i=\begin{bmatrix} 1 & \rho & \rho^2 & \rho^3 & \rho^4 \\ \rho & 1 & \rho & \rho^2 & \rho^3 \\ \rho^2 & \rho & 1 & \rho & \rho^2 \\ \rho^3 & \rho^2 & \rho & 1 & \rho \\ \rho^4 & \rho^3 & \rho^2 & \rho & 1 \end{bmatrix}
　　这种相关称为1阶自相关(first order autocorrelation)。或更广义地，两次观察值间的相关与观察时间间隔有关：
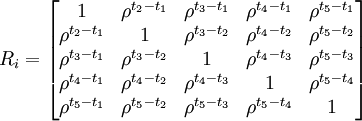
R_i=\begin{bmatrix} 1 & \rho^{t_2-t_1} & \rho^{t_3-t_1} & \rho^{t_4-t_1} & \rho^{t_5-t_1} \\ \rho^{t_2-t_1} & 1 & \rho^{t_3-t_2} & \rho^{t_4-t_2} & \rho^{t_5-t_2} \\ \rho^{t_3-t_1} & \rho^{t_3-t_2} & 1 & \rho^{t_4-t_3} & \rho^{t_5-t_3} \\ \rho^{t_4-t_1} & \rho^{t_4-t_2} & \rho^{t_4-t_3} & 1 & \rho^{t_5-t_4} \\ \rho^{t_5-t_1} & \rho^{t_5-t_2} & \rho^{t_5-t_3} & \rho^{t_5-t_4} & 1 \end{bmatrix}

　　4．非确定相关(unstructured，general structure)即相关矩阵的非对角线上的元素均不等。

　　5．独立(independent，zero correlation)即块矩阵A的非对角线上的元素均为0。

　　虽然组内相关矩阵结构的选择可借助于统计学方法进行判断，但对具体资料，笔者建议按专业知识来确定其结构。

[编辑]

相关矩阵分析法[3]

　　相关矩阵分析法是20世纪70年代初，联合国教科文组织在各国专家的协助下，建立和发展起来的一套确定科技优先发展领域的系统性方法。其核心就是在技术专家协助下，编制和分析D／D矩阵(发展目标之间的相关矩阵)、S／D矩阵(学科领域与发展目标的相关矩阵)和S／S矩阵(学科领域之间的相关矩阵)，该方法运用的关键是：①确定好问题的边界(发展目标和科技领域条目划分)；②设计好专家调查表(科学、合理、简便)，选择好咨询专家；③做好三个相关矩阵的构造和系统分析。

[编辑]

相关矩阵的案例分析

[编辑]

案例一：[4]

　　通过考查相关矩阵来研究广告费、销售量和每加仑价格之间的关系。相关矩阵通过计算各对变量相互间的简单相关系数来构造。

　　相关矩阵实例如表1所示。代表变量1和变量2之间关系的相关系数表示为r12。注意，第一个下标1指在表格中所在的行，第二个下标2指在表格中所在的列。这一方法使人一眼就能确定任何两个变量之间的关系。当然，变量1和变量2之间的相关性与变量2和变量1之间的相关性相同，即r12 = r21。因此，只需要1／2的相关矩阵。此外，一个变量与它本身的相关性总是等于1，例如r11 = r22 = r33 = 1。

　　用计算机运行数据，所得到的相关矩阵如表2所示。对广告费、销售量和每加仑价格之间关系的调查显示，新的自变量有助于改进预测结果。相关矩阵显示，广告费与因变量(销售量)有很高的正相关性(r13 = 0.89)，与自变量(每加仑价格)有比较适度的负相关性(r23 = − 0.65)。这一相互关系的组合可以由广告费来解释一些不能被每加仑价格解释的销售量的总方差。我们将会看到，当同时使用每加仑价格和广告费来估算销售量时，R2增加到了93．2％。

　　相关矩阵的分析对涉及多个自变量问题的解决是重要的开始步骤。

表1 相关矩阵

变量
变量123
1r11r12r13
2r21r22r23
3r31r32r33

表2 数据的相关矩阵

变量
变量销售额
1		价格
2		广告费
3
销售额11.00-0.860.89
价格21.00-0.65
广告费31.00
[编辑]

相关条目

[编辑]

参考文献

  1. ↑ 车文博主编.当代西方心理学新词典.吉林人民出版社,2001年10月第1版.
  2. ↑ 饶克勤主编.第五章 广义估计方程和多水平模型 卫生统计方法与应用进展第二卷.人民卫生出版社,2008.1.
  3. ↑ 吴乐山,孙建中主编 第五章 军事医学科学技术选择和评估 现代军事医学战略研究.军事医学科学出版社,2004年08月第1版.
  4. ↑ (美)约翰·E.汉克 迪恩·W.威切恩著 胡晓凤译.第七章 多元回归分析 管理学系列 商业预测（第八版）.清华大学出版社,2006年07月第1版.
来自"https://wiki.mbalib.com/wiki/%E7%9B%B8%E5%85%B3%E7%9F%A9%E9%98%B5"
打开MBA智库App, 阅读完整内容 打开App
本条目对我有帮助20
赏
MBA智库APP

扫一扫，下载MBA智库APP

分享到：
  如果您认为本条目还有待完善，需要补充新内容或修改错误内容，请编辑条目或投诉举报。

本条目由以下用户参与贡献

李漠,连晓雾.

评论(共0条)

提示:评论内容为网友针对条目"相关矩阵"展开的讨论，与本站观点立场无关。

发表评论请文明上网，理性发言并遵守有关规定。

百科VIP
百科VIP会员权益

  • 无广告阅读

  • 免验证复制

开通/续费百科VIP

消息

昵称未设置
百科VIP

未开通

收藏夹

账号安全中心

我的页面

我的贡献

我的讨论页

我的设置
退出登录
打开APP

以上内容根据网友推荐自动排序生成

下载APP

闽公网安备 35020302032707号