期權估價法
出自 MBA智库百科(https://wiki.mbalib.com/)
目錄 |
什麼是期權估價法[1]
所謂期權估價法,是指充分考慮企業在未來經營中存在的投資機會或擁有的選擇權的價值,進而評估企業價值的一種方法。它是20世紀70年代後在期權估價理論的基礎上發展起來的。
期權估價法的優缺點[1]
優點:
隨著信息技術及相關產業的迅猛發展,企業在經營中面臨越來越多的不確定性和風險,也面臨大量的投資機會和發展機會,在此背景下出現的期權估價理論給企業價值評估提供了一種新思路,在此理論指導下建立起來的期權估價方法也為企業估價提供了一種有意義的工具。與傳統估價方法相比,期權估價法考慮並計算未來機會及選擇權的價值,從而拓寬投資決策的思路,使企業估價更為科學合理。
缺點:
期權估價法在實際應用過程中還受到許多條件的制約。例如,Black-Scholes期權定價模型是在一系列前提假設的基礎上建立和發展起來的,這些假設在現實中很少能夠得到完全實現。該模型是對現實問題的簡化和抽象,是對現實狀況儘可能相對地模擬,但很難做到與實際情況完全一致。此外,任何一種期權定價模型,在實際運用中都是複雜和繁瑣的。
期權估價法與傳統估價法之比較[2]
期權估價法及與傳統估價法的比較客觀地說,並不相互排斥。“對於期權估價法是否會完全取代現金流折現法來評估公司整體價值現在還沒有定論”。但可以肯定:資產法尋找“可比”資產在實際操作中的困難和通常被作為“次級”信息來使用的現實使其在實際應用中無法和現金流折現法一樣受推崇。而收益法使用會計利潤的致命缺陷和尋找在增長前景、風險性、財務結構具有可比性的上市公司市盈率的難度,同樣限制了它在公司價值評估中的作用。對於目前廣泛使用的現金流折現法,由於適合採用現金流折現方法(被估價資產當前的現金流為正,並可以比較可靠地估計未來現金流的發生時間,同時,根據現金流的風險性又能夠確定恰當的折現率)的條件往往不能得到滿足,使得使用現金流折現法進行估價遇到比較大的困難。
與傳統估價法對比,期權估價法減輕了尋找“同比”指標的難度,並保留了現金流折現的長處,特別是具有對確定性的“自然適應性”,解決了目前技術公司(如網路、生物公司)上市定價、公司併購估價等目前資本市場常見的難題。“即使是在傳統估價方法適合的情況下,期權估價法仍提供了另一種有價值的視角”。因此如本章第一節所論述,在公司併購或重組時存在的三項不確定性,成為現金流折現無法迴避的難題。而這些不能通過傳統的現金流折現法進行估價,作為不確定環境下的估價利器——期權估價法(如用實物期權為公司投資項目估價就是一例)既是估價理論的突破又是實踐的客觀需要。
期權估價法的應用[1]
期權估價法在高新技術企業中的應用主要包括以下幾類:
a) 產品專利。
當高新技術企業擁有的專利未投入商品生產,預期的現金流量具有較大的不確定性,且近期不一定會產生現金流量時,可以將該專利視為一種帶有期權性質的資產,企業在開發該項專利的過程中發生的研究費用與註冊費用視為期權費,企業擁有專利後就擁有了開發和製造該項專利產品的權利。企業是否追加後續投資,取決於對該專利產品未來產生的現金流量的預期。此時可將專利權視為看漲期權進行評估,產品本身為標的資產,追加的投資為期權的執行價格。
b) 研究開發費用。
高新技術企業的研究開發費用在其總支出中所占比例較大,這也是高新技術企業區別於傳統企業的地方。與專利權相似,研發成果也可以視為一項看漲期權。
在這種情況下,可以把股權視為以企業為標的資產的看漲期權,其執行價格為流通在外的債務的價值,當企業預期價值(即所有者權益價值)超過債務價值時,則股東可清算。根據該方法衡量出來的企業價值,也許能夠解釋為什麼那些處在困境中的高新技術企業在兼併中仍能取得高於其賬麵價值的補償。
增長型企業的期權估價模型[3]
1.具有單一投資機會的期權估價
在考慮了投資機會的期權價值評估體系下,企業價值表示為:vt = vf + vc,vf是現有業務現金流量的貼現值,vc為未來投資機會的期權價值,由Black—Scholes公式進行計算。
具體計算步驟如下:
(1)計算現有業務現金流量的貼現值: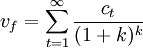 (1)
(1)
其中,ct表示計算期內第t年的現金流量,k表示企業的加權平均資本成本。
(2)計算投資機會的期權值:vc = Sn(d1) − Xe − rtN(d2)(2)
其中,![d_1=\frac{\left[Ln(\frac{S}{X})+(r+\frac{\delta^2}{2})\right]}{(\delta \sqrt{t_0})}](/w/images/math/f/d/5/fd546cf59224484244fb0691fd8277d6.png) ;
;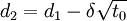
式中S表示投資機會期權標的資產的當前價值,由項目投資產生的凈現金流貼現到預測期初得到;X表示標的資產的行使價值,即項目的投資額;r表示無風險利率;δ表示資產收益波動率;t表示投資機會期權執行日到預測期初的時間,即投資期權有效期。
2.具有序列投資機會的企業估價
企業的增長機會可以被看作為基於現實資本的看漲期權。所以,在企業發展的不同時點上都有一個單獨的增長期權;當企業在每個發展時點上都持有增長期權時,便構成了序列增長期權。由於序列增長期權中的前後期單獨期權是相互依賴的(後期投資受前期投資的影響),而且期權數目隨企業存續期的延長而增多,因此無法直接應用常規法進行計算,必須尋找新的求解方法。
把企業的一個增長機會視為一項標的資產是投資項目、有效期為T的歐式看漲期權,在t時刻有效期為τ的增長期權的道奇收益為Rt(τ):
Rt(T) = max(Pt + T − It + T,0)(3)
其中Pt + τ為t + τ時刻執行期權、進行投資的項目價值,It + τ為t + τ時刻執行期權的投資成本。
由於投資項目的價值Pt是投資產生現金流的折現,所以把Pt看作為每單位時間現金流價值π的函數。假設在風險中性世界中,π服從幾何布朗運動: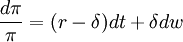 (4)
(4)
其中,r為π的均衡期望回報率,表現為無風險利率;δ為與標的資產非流動性程度正相關的報酬率虧空,是一恆量。因此r − δ表示π的瞬時期望增長率,δ表示瞬時波動率,dw是維納過程。
由(4)式可知在時期t的期望現金流為E(πt) = π0e(r − δ)t,其中\pi_0為投資項目的初始現金流量。投資項目的價值應等於所有單位時間現金流\pi以風險利率貼現價值的總和,即: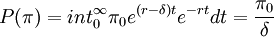 (5)
(5)
假設每一個投資項目中δ是恆量,則在t + τ時刻的投資項目的價值為:
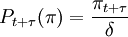 (6)
(6)
其中,Pt + τ表示在t+\tau時刻投資項目的價值,πt + π,0表示投資項目t + τ時刻的初始現金流。
將(11)代入(8),得到t時刻、有效期為τ的成長期權的期滿收益為:
![R_t(\tau)=\left[(\frac{\pi_{t+\tau,0}}{\delta}-I_{t+\tau}),0\right]](/w/images/math/5/f/9/5f9e3df1ef013ea9763de2cff1c2329e.png) (7)
(7)
令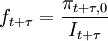 ;
;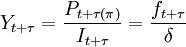
則ft + τ表示在t + τ時刻投資項目的初始投資收益率,Yt + τ表示在t + τ時刻每單位投資的收益率,代入(12)式,整理得:
![R_t(\tau)=I_{t+\tau}\max\left[Y_{t+\tau-1,0}\right]](/w/images/math/e/c/3/ec30d19bdda46d17513d198c66d3af2b.png) (8)
(8)
在風險中性世界里,t時刻增長期權的現值Rt,即為它的期望收益用無風險利率進行折現:
![R_t=-e^{-r(t+\tau)}E\left\{I_{t+\tau}\max\left[Y_{t+\tau}-1,0\right]\right\}](/w/images/math/6/7/1/671017b94e18296601a80ebee47d7843.png) (9)
(9)
企業價值可以表示為現實資產收益的現值與持有的序列期權現值的和,考慮到無限生命期,則預測初的企業價值可以表示為:
![v_f=\sum^\infty_{i=1}\left[e^{-r i}E(C_i)+R_{i-1}\right]](/w/images/math/f/c/9/fc91742b1e80753b8c6c270615584cfa.png) (10)
(10)
其中,Ci表示在風險中性概率下企業現實資產在第i期產生的隨機現金流;Ri − 1表示企業在i-1時刻持有的成長期權的現值。
假設企業持有的每一個成長期權的有效期為1(τ = 1),由(9)式得,企業字第i-1時刻持有的增長期權的現值為:
![R_{i-1}=e^{-r i}E\left\{I_i \max\left[Y_i-1,0\right]\right\}](/w/images/math/f/d/7/fd72b4c24beaa232f938c01e6ea1c035.png) (11)
(11)
將(11)式代入(10)式,並考慮到(3)式,It = bCt,得到預測期初的企業價值為:
![v_f=\sum^\infty_{i=1}e^{-r i}\left\{E(C_i)+\left[b C_i \max(Y_{i-1},0)\right]\right\}](/w/images/math/2/c/1/2c1fb01416104e96f70f527cf898992f.png) (12)
(12)
採用Monte Carlo模擬的方法,即可對上式進行求解。







