區間估計
出自 MBA智库百科(https://wiki.mbalib.com/)
區間估計(Interval Estimation)
目錄 |
區間估計就是以一定的概率保證估計包含總體參數的一個值域,即根據樣本指標和抽樣平均誤差推斷總體指標的可能範圍。它包括兩部分內容:一是這一可能範圍的大小;二是總體指標落在這個可能範圍內的概率。區間估計既說清估計結果的準確程度,又同時表明這個估計結果的可靠程度,所以區間估計是比較科學的。
用樣本指標來估計總體指標,要達到100%的準確而沒有任何誤差,幾乎是不可能的,所以在估計總體指標時就必須同時考慮估計誤差的大小。從人們的主觀願望上看,總是希望花較少的錢取得較好的效果,也就是說希望調查費用和調查誤差越小越好。但是,在其他條件不變的情況下,縮小抽樣誤差就意味著增加調查費用,它們是一對矛盾。因此,在進行抽樣調查時,應該根據研究目的和任務以及研究對象的標誌變異程度,科學確定允許的誤差範圍。
區間估計必須同時具備三個要素。即具備估計值、抽樣極限誤差和概率保證程度三個基本要素。
抽樣誤差範圍決定抽樣估計的準確性,概率保證程度決定抽樣估計的可靠性,二者密切聯繫,但同時又是一對矛盾,所以,對估計的精確度和可靠性的要求應慎重考慮。
在實際抽樣調查中,區間估計根據給定的條件不同,有兩種估計方法:①給定極限誤差,要求對總體指標做出區間估計;②給定概率保證程度,要求對總體指標做出區間估計。
例1:某企業對某批電子元件進行檢驗,隨機抽取100只,測得平均耐用時間為1000小時,標準差為50小時,合格率為94%,求:
(1)以耐用時間的允許誤差範圍Δx=10小時,估計該批產品平均耐用時間的區間及其概率保證程度。
(2)以合格率估計的誤差範圍不超過2.45%,估計該批產品合格率的區間及其概率保證程度。
(3)試以95%的概率保證程度,對該批產品的平均耐用時間做出區間估計。
(4)試以95%的概率保證程度,對該批產品的合格率做出區間估計。
求(1)的計算步驟:
①求樣本指標:
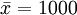 (小時) σ = 50(小時)
(小時) σ = 50(小時)
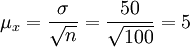 (小時)
(小時)
②根據給定的Δx=10小時,計算總體平均數的上、下限:
- 下限
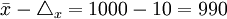 (小時)
(小時)
- 上限
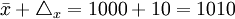 (小時)
(小時)
③根據t=Δx/μx=10/5=2,查概率表得F(t)=95.45% 由以上計算結果,估計該批產品的平均耐用時間在990~1010小時之間,有95.45%的概率保證程度。
求(2)的計算步驟:
①求樣本指標:
- p=94%
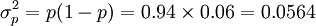
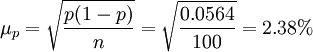
②根據給定的Δp=2.45%,求總體合格率的上、下限:
- 下限
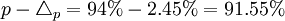
- 上限
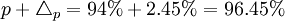
③根據t=Δp /μp=2.45%/2.38%=1.03,查概率表得F(t)=69.70%
由以上計算結果,估計該批產品的合格率在91.55%~96.45%之間,有69.70%的概率保證程度。
解:求(3)的計算步驟:
①求樣本指標:
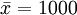 (小時) σ = 50(小時)
(小時) σ = 50(小時)
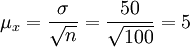 (小時)
(小時)
②根據給定的F(t)=95%,查概率表得t=1.96。
③根據Δx=t×μx=1.96×5=9.8,計算總體平均耐用時間的上、下限:
- 下限
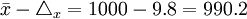 (小時)
(小時)
- 上限
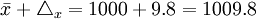
所以,以95%的概率保證程度估計該批產品的平均耐用時間在990.2~1009.8小時之間。
求(4)的計算步驟:
①求樣本指標:
- p=94%
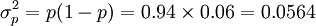
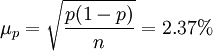
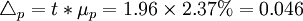
②下限p-Δp=94%-4.6%=89.4%
上限p+Δp=94%+4.6%=98.6%。
所以,以95%的概率保證程度估計該批產品的合格率在89.4%~98.6%之間。
(一)當σ2已知時,求μ的置信區間
例2:某種零件的長度服從正態分佈,從該批產品中隨機抽取9件,測得它們的平均長度為21.4毫米,已知總體標準差為σ = 0.15毫米,試建立該種零件平均長度的置信區間,假定給定置信水平為0.95。
解:已知X~N(μ,0.152), ,n=9,1-α=0.95,因為
,n=9,1-α=0.95,因為
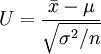 ~N(0,1)
~N(0,1)
所以對於給定的置信水平0.95,有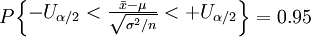 。
。
當α=0.05時,Uα/2=1.96,於是有
即總體均值的置信區間為[21.302,21.498]。
我們有95%的概率保證該種零件的平均長度在21.302毫米和21.498毫米之間。
例3:某保險公司自投保人中隨機抽取36人,計算出此36人的平均年齡 =39.5歲,已知投保人年齡分佈近似正態分佈,標準差為7.2歲,試求所有投保人平均年齡的置信區間(1-α=99%)。
解:已知,X~N(μ,7.22),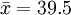 歲,n=36,1-α=0.99,則
歲,n=36,1-α=0.99,則
當α=0.01,有Uα / 2 = U0.01 / 2 = U0.005 = 2.575,所以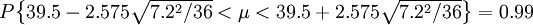 ,即總體的置信區間為[36.41,42.59]。有99%的把握保證投保人的平均年齡在36~42歲之間。
,即總體的置信區間為[36.41,42.59]。有99%的把握保證投保人的平均年齡在36~42歲之間。
(二)當 2未知時,求μ的置信區間
不知道總體方差時,一個很自然的想法是用樣本方差來代替,這時,需要考慮的問題是,用樣本方差代替總體方差後,統計量 服從的是什麼分佈,以下定理給出了統計量T的分佈形式。
定理 設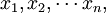 (n≥2)是來自總體N(μ,σ2)的一個樣本,則
(n≥2)是來自總體N(μ,σ2)的一個樣本,則
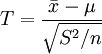 ~t(n-1)
~t(n-1)
t分佈具有如下特性:
1、t分佈與標準正態分佈相似,是以x=0為對稱軸的鐘形對稱分佈,取值範圍是(-∞,+∞),但是t分佈的方差大於1,比標準正態分佈的方差大,所以從分佈曲線看,t分佈的曲線較標準正態分佈平緩。
2、t分佈的密度函數為
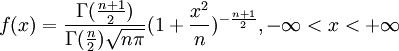
t分佈的密度函數中只有一個參數,稱為自由度。如果隨機變數X具有以上形式的分佈密度,則稱X服從自由度為n的t分佈,記為X~t(n)。隨著自由度的增大,t分佈的變異程度逐漸減小,其方差逐漸接近1,當n→∞時,t分佈成為正態分佈。
3、隨機變數X落在某一區域內的概率,等於t分佈曲線下,相應區域的面積,對於不同的n,同樣的區域下的概率不同。如n=10,X落入[-1.372,+1.372]區間的概率為0.9,而當n=20時,概率為0.9所對應的區間為[-1.325,+1.325];當n=30時,概率為0.9所對應的區間為[-1.31,+1.31]。
關於t分佈的特性就討論到此,現在回到如何應用t分佈求解置信區間的問題,既然定理已經證明瞭統計量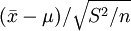 服從n-1個自由度的t分佈,則對於給定的顯著性水平α,不難找出tα / 2(n − 1),使得
服從n-1個自由度的t分佈,則對於給定的顯著性水平α,不難找出tα / 2(n − 1),使得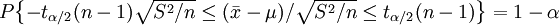 。於是得到以1-α置信水平保證的置信區間
。於是得到以1-α置信水平保證的置信區間
![[\bar{x}-t_{\alpha/2}(n-1)\sqrt{S^2/n},\bar{x}+t_{\alpha/2}(n-1)\sqrt{S^2/n}]](/w/images/math/3/1/3/313e829c656977b4b91f6d07d4667ef7.png)
例4:某研究機構進行了一項調查來估計吸煙者一月花在抽煙上的平均支出,假定吸煙者買煙的月支出近似服從正態分佈。該機構隨機抽取了容量為26的樣本進行調查,得到樣本平均數為80元,樣本標準差為20元,試以95%的把握估計全部吸煙者月均煙錢支出的置信區間。
解:已知 =80,S=20,n=26,1-α=0.95
=80,S=20,n=26,1-α=0.95
由於不知道總體方差,所以用樣本方差代替。因為
根據α=0.05,查閱t分佈表得,t0.05 / 2(25)=2.06。
所以有 ={80-2.06(3.92)<μ<80+2.06(3.92)}=0.95,即總體的置信區間為[71.92,88.08]。
={80-2.06(3.92)<μ<80+2.06(3.92)}=0.95,即總體的置信區間為[71.92,88.08]。
有95%的把握認為吸煙者月均煙錢支出在71.92元到88.08元之間。
(三)單個非正態總體或總體分佈未知,求U的置信區間
當總體為非正態分佈,或不知總體的分佈形式時,只要知道總體方差,則根據Lindeberg-Levy的中心極限定理,當n很大時,統計量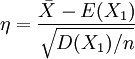 就近似服從標準正態分佈,經驗上,n>30就可以認為是大樣本了。
就近似服從標準正態分佈,經驗上,n>30就可以認為是大樣本了。
例5:設某金融機構共有8042張應收賬款單,根據過去記錄,所有應收賬款的標準差為3033.4元。現隨機抽查了250張應收款單,得平均應收款為3319元,求98%置信水平的平均應收款。
解:已知 =3319元,n=250>30,1-α=0.98,σ=3033.4
=3319元,n=250>30,1-α=0.98,σ=3033.4
因為 近似服從標準正態分佈,Uα / 2 = U0.02 / 2 = 2.33,則總體均值的置信區間為
近似服從標準正態分佈,Uα / 2 = U0.02 / 2 = 2.33,則總體均值的置信區間為
![[\bar{x}-U_{\alpha/2}\sqrt{\sigma^2/n},\bar{x}+U_{\alpha/2}\sqrt{\sigma^2/n}]](/w/images/math/9/3/b/93b40f27e86bea50971d28582ffbd841.png)
- =[3319-2.33(3033.4/\sqrt{250}),3319+2.33(3033.4/\sqrt{250})
- =[2871.99,3766]
根據調查結果,我們有98%的把握認為全部賬單的平均金額至少為2871.99元,至多為3766元。
以上例題雖然不知總體分佈形式,但總體的方差是已知的,而在實際中往往並不知道總體的方差,在實際應用中,只要是大樣本,則仍然可以用樣本方差代替統計量η中的總體方差,並以標準正態分佈近似作為統計量η的抽樣分佈。
例6:某地區抽查了400戶農民家庭的人均化纖布的消費量,得到平均值為3.3米,標準差為0.9米,試以95%的置信水平估計該地區農民家庭人均化纖布的消費量。
解:因為n=400是大樣本,則有
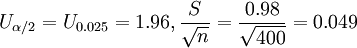
- P{3.3-1.96(0.049)<μ<3.3+1.96(0.049)}
- =P{3.204<μ<3.396}=0.95
置們區間為[3.204,3.396]。
所以,有95%的把握認為該地區農民化纖布的消費量在3.204米至3.396米之間。








謝謝 還有例題 好貼心 :)