固定樣本量抽樣

用手机看条目

出自 MBA智库百科(https://wiki.mbalib.com/)

(重定向自固定样本规模抽样)

什麼是固定樣本量抽樣

　　固定樣本量抽樣也叫固定樣本規模抽樣，是一種基本的最為廣泛的屬性抽樣方法。他根據公式或表格確定固定的樣本數量進行審查，並以全部樣本審查結果推斷總體的一種審計抽樣方法。

[編輯]

固定樣本量抽樣的步驟

　　利用固定樣本量抽樣進行內部控制符合性測試的步驟如下：

　　(1)確定審計的目的和抽樣總體

　　(2)定義“違反”的標準

　　(3)確定抽樣要求的可靠程度、可容忍的最大誤差率(即精確度上限)和總體預期的誤差率。

　　(4)確定樣本量

　　固定樣本量抽樣的樣本量確定

　　(I)查表法

　　①按要求的可靠程度選定要查的表。

　　②在表的頂行上找到最大可容忍的誤差率，在表最左邊一欄找到總體預期的誤差率，兩者的交點處為要求的樣本量。

　　(II)計演算法:n=t2P(1-P)/△2

　　式中：

　　n——樣本量

　　t——正態標準差

　　P——預計總體的誤差率

　　△——精確度

　　固定樣本量抽樣的樣本量確定

　　上述查表或計算得到的結果都是考慮總體量N遠大於樣本量n的情況。若n/N較大時，實際審查的樣本量還可以修正為：n/(1+n/N)

　　(5)選取並審查樣本

　　(6)從樣本的審查結果推斷總體

　　樣本發現的誤差率小於或等於總體預計的違反率，因而可導出此項內部控制有效，可以依賴的結論。

　　樣本發現誤差率大於總體預計的誤差率。此項內部控制無效，應擴大相應的實質性審查。

[編輯]

固定樣本量抽樣的數理基礎

　　審計中使用的固定樣本量抽樣，就是從被審計對象總體中隨機地抽取n個個體構成一個樣本，並且規定一個誤差數目c，如果對被抽選的樣本審計後發現有誤差的個體數目e<c，則判斷被審計對象總體是可以接受的；反之，如果對被抽選的樣本審計後有誤差的個體數目e>c，則判斷被審計對象總體應該予以拒絕。在這裡c是允許誤差的個數，稱之為接受數，這樣固定樣本量抽樣就可以用兩個數c和n來表示，記做(n|c)。

　　設有總體單位數為N的被審計總體，從中抽取大小為n的一個樣本，假定被審計總體中存在誤差的比率為P，如果我們採用固定樣本量抽樣方法(n|c)來審計被審計總體，當P=0時肯定可以判斷接受被審計對象；而當P=1時肯定拒絕被審計對象，但是當0<P<1時可能接受也可能拒絕；錯誤率P越接近於0，接受的可能性越大；而P值越接近於1時，接受的可能性就越小，這種接受可能性大小可以用接受概率來表示，只要抽樣審計方案確定了，則接受概率只依賴於P。

　　假如規定：當被審計對象總體錯誤比率P不超過 $P 0$ 時，該被審計對象就可以被接受；那麼一個理想的抽樣審計方案應當滿足：當P≤ $P 0$ 時接受被審計對象總體的概率等於1；當P>P。時接受概率等於0。但是，這種理想的抽樣審計方案現實中並不存在，即使採用全面詳細審計，也可能發生人為錯誤的情況。因此，一個抽樣審計方案如果能滿足以下特點，那麼它就是一個很好的抽樣審計方案：當被審計對象總體中錯誤比率較低時，則以高概率接受被審計對象總體；當被審計對象總體中錯誤比率較高時，接受概率迅速減小，當其錯誤率高到某個規定限度時將以高概率拒絕被審計對象總體。

　　(一)抽樣審計特征函數

　　在前面的討論中知道，對任何一個確定的抽樣審計方案來說，接受概率是總體錯誤比率P的函數，那麼用L(P)來表示，則稱L(P)是屬性抽樣審計的特征函數，利用抽樣審計特征函數就可以做出抽樣審計特征曲線，藉以判斷一個抽樣審計方案的優劣。

　　1、有限總體時抽樣審計特征函數

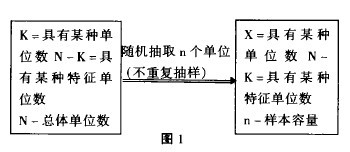
　　假設被審計對象總體有N單位組成，我們採用(n|c)方案來抽樣審計該審計對象總體；假設該審計對象總體的錯誤比率為P，用L(P)表示抽樣審計特征函數，為了決定函數L(P)的形式，首先計算“在樣本中屬性個數X=x這個事件出現的概率，其用P(X=x)表示。這裡的P與前面出現的P意義不同，這裡的P不表示總體錯誤比率，而是用來表示在抽取的n個體組成的樣本中出現x錯誤的概率。超幾何分佈適合於下麵的試驗情況：在一個有N單位的有限總體中，每一個單位可以根據其是否具有某種特征而歸入兩類中的一類，用不重覆抽樣的方式從中抽取n單位，如果令x表示樣本中具有某種特征的單位數，則隨機變數x服從超幾何分佈。用圖1表示。

　　根據審計實踐知，內部控制測試中審計總體具有超幾何分佈所要求的條件，可以利用超幾何概率分佈來處理這類審計總體，下麵首先介紹超幾何概率分佈。

　　(1)利用超幾何概率分佈計算P(X=x)

　　因為總體為N，錯誤比率為P，則該總體中錯誤屬性的總數為N×P，記作k=N×Po出現屬性x：x事件，相當於在大小為n的樣本中有x單位是從k單位具有某種屬性的項目中抽取的，同時，在樣本中另外n-x單位是從總體中N-k不具有這種屬性的項目中抽出的，從項目k中抽出x項目的所有可能組合有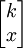 $\begin{bmatrix} k \\ x \end{bmatrix}$ 種，從N-k項目中抽取n-x項目的所有可能組合有 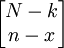$\begin{bmatrix} N-k \\ n-x \end{bmatrix}$ 種，所以在一個大小為n的樣本中恰好包含x單位的可能組合共有 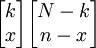$\begin{bmatrix} k \\ x \end{bmatrix} \begin{bmatrix} N-k \\ n-x \end{bmatrix}$ 種；另一方面，從N個總體項目中抽取n個樣本項目的可能組合共有 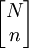$\begin{bmatrix} N \\ n \end{bmatrix}$ 種。因此有：

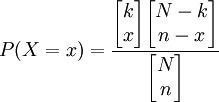　　 $P(X=x)=\frac{\begin{bmatrix} k \\ x \end{bmatrix} \begin{bmatrix} N-k \\ n-x \end{bmatrix}}{\begin{bmatrix} N \\ n \end{bmatrix}}$ 　　(1)

　　由此可見，當N、k和n確定之後，P(X=x)只依賴於x，記為：

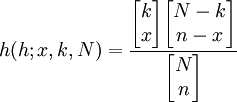　　 $h(h;x,k,N)=\frac{\begin{bmatrix} k \\ x \end{bmatrix} \begin{bmatrix} N-k \\ n-x \end{bmatrix}}{\begin{bmatrix} N \\ n \end{bmatrix}}$ 　　(2)

　　其中，X的可能取值為0，1，2，3...．min(k，n)，所以：

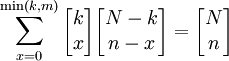　　 $\sum_{x=0}^{\min(k,m)} \begin{bmatrix} k \\ x \end{bmatrix} \begin{bmatrix} N-k \\ n-x \end{bmatrix}=\begin{bmatrix} N \\ n \end{bmatrix}$ 　　(3)

　　將上式兩端除以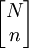 $\begin{bmatrix} N \\ n \end{bmatrix}$ 即得：

　　 $\sum_{x=0}^{\min(k,m)} h(x;n,k,N)=1$ 　　(4)

　　我們稱h(x；n，k，N)為“超幾何概率分佈”。

　　當我們採用方案(n|c)抽樣審計被審計對象時，只要樣本中錯誤出現的次數x不超過c，則認為可以接受被審計對象。在總體錯誤率為P時的接受概率可由(5)給出：

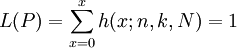　　 $L(P)=\sum_{x=0}^x h(x;n,k,N)=1$ 　　(5)式中：K=N×P

　　由上式(5)所確定的函數L(P)即為方案(n|c)的抽樣審計特征函數。如果以P為橫坐標，以L(P)為縱坐標，將點(P，L(P))繪在平面上即可得到一條曲線，該條曲線就是方案(n|c)的抽樣審計特征曲線。

　　(2)利用二項分佈求近似值

　　超幾何分佈與二項分佈的區別在於抽樣方式不同，但兩者具有相近的性質。從分佈特征值看，他們的均值是相同的，超幾何分佈的方差是二項分佈的方差乘一個修正繫數(N-n)/(N-1)，這一繫數總是小於1。這說明超幾何分佈比二項分佈要集中，因此如果要估計在均值上下一定範圍內的概率時，可以用二項分佈近似計算超幾何分佈的概率。上述超幾何分佈概率的求解過程相當複雜，如果審計總體能夠滿足下麵的條件，可以利用二項分佈作為超幾何分佈的有效近似，即樣本容量不超過總體的十分之一，n/N≤0．1，就可以用下麵所示的近似公式來計算h(x;n,k,N)：

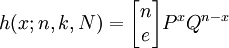　　 $h(x;n,k,N)=\begin{bmatrix} n \\ e \end{bmatrix} P^xQ^{n-x}$ 　　(6)

　　其中。Q=1-P

　　我們記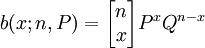 $b(x;n,P)=\begin{bmatrix} n \\ x \end{bmatrix} P^xQ^{n-x}$ ，其為 $(P + Q) n$ 的二項展開式一般項，顯然：

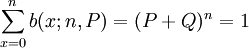　　 $\sum_{x=0}^n b(x;n,P)=(P+Q)^n=1$ 　　(7)

　　我們稱b(x;n,P)為二項概率分佈，其具體值可以查二項分佈表求得。將(6)代A(2-5)，即有：

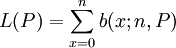　　 $L(P)=\sum_{x=0}^n b(x;n,P)$ 　　(8)

　　(3)可以利用普阿松分佈求近似值

　　從歷史發展看，普阿松分佈最初是由法國數學家西蒙· 普阿松作為二項分佈的近似計算提出來的。當二項分佈的概率P很小，而實驗次數n又很大時，計算二項分佈相當複雜，但這時的二項分佈近似於普阿松分佈，而用普阿松分佈來計算要方便得多。只要樣本量n比較大，並且滿足n≤N/10，P≤0.1兩個條件，也可以利用普阿松分佈作為超幾何分佈的近似。h(x;n,k,N)和 $L(P)h(x;n,k,N)=\frac{\lambda^k}{x}[x]^{-\lambda}$ 　　(9)

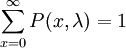　　可以證明： $\sum_{x=0}^\infty P(x,\lambda)=1$ =0

　　 $P (x;λ)$ 稱為普阿松分佈，其具體數值可以在普阿松分佈表中查得。

　　(二)無限總體時抽樣審計特征函數

　　儘管審計總體總是有限的，但是當審計總體特別大的時候，我們也可以將其作為無限總體處理，這樣的結果是既簡化計算，又不失為一個很好的近似。我們考慮從一個錯誤比率為P的無限總體中隨機抽取n個樣本項目，其中出現x個錯誤的情形共有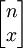 $\begin{bmatrix} n \\ x \end{bmatrix}$ 種，出現每種可能情形的概率都是 $P x Q n - x$ ，所以在樣本量為n的樣本中出現錯誤次數x的概率為：

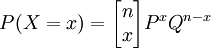
　　 $P(X=x)=\begin{bmatrix} n \\ x \end{bmatrix} P^x Q^{n-x}$

　　即當總體為無限時，樣本中出現錯誤的次數是遵照二項分佈，因此，抽樣審計方案(n|c)的抽樣審計特征函數為：

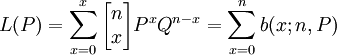
　　 $L(P)=\sum_{x=0}^x \begin{bmatrix} n \\ x \end{bmatrix} P^x Q^{n-x}=\sum_{x=0}^n b(x;n,P)$

　　固定樣本量抽樣、連續抽樣和發現抽樣的有關表格通常是建立在上述有關分佈基礎之上，為了計算的方便，通常是以二項分佈為基礎，並且假定採取重覆抽樣。

[編輯]

本条目由以下用户参与贡献

Dan,鲈鱼,连晓雾.

頁面分類: 審計術語

評論(共0條)

提示:評論內容為網友針對條目"固定樣本量抽樣"展開的討論，與本站觀點立場無關。

發表評論請文明上網，理性發言並遵守有關規定。

查看

工具▼

固定樣本量抽樣

出自 MBA智库百科(https://wiki.mbalib.com/)

目錄

什麼是固定樣本量抽樣

固定樣本量抽樣的步驟

固定樣本量抽樣的數理基礎

相關條目

温馨提示

本条目相关课程

本条目由以下用户参与贡献

評論(共0條)

導航

意见反馈

查看

工具▼

固定樣本量抽樣

出自 MBA智库百科(https://wiki.mbalib.com/)

目錄

什麼是固定樣本量抽樣

固定樣本量抽樣的步驟

固定樣本量抽樣的數理基礎

相關條目

温馨提示

本條目相關文檔

本条目相关课程

本条目由以下用户参与贡献

評論(共0條)

導航

意见反馈