凸性
出自 MBA智库百科(https://wiki.mbalib.com/)
凸性（convexity）
目錄 |
如果一種債券的市場價格等於它的面值，它的到期收益率就等於息票利率；如果市場價格高於（低於）面值，則到期收益率就會低於（高於）息票利率。據此，可以導出債券定價的兩個基本特點：第一，如果債券價格上漲，則收益率必然下降，反之，如果債券價格下降，則收益率必然上升；第二，債券收益率的下降會引起債券價格的上升，且上升的幅度要超過債券收益率以同樣比率上升引起的債券價格下降幅度。
根據第一條，債券價格與收益率呈反向關係；根據第二條，不僅表明二者的關係是非線性的，而且債券價格與收益率呈凸關係，這種關係常常被稱為債券價格的凸性（convexity）。
凸性是指在某一到期收益率下,到期收益率發生變動而引起的價格變動幅度的變動程度。凸性是對債券價格曲線彎曲程度的一種度量。凸性的出現是為了彌補久期本身也會隨著利率的變化而變化的不足。因為在利率變化比較大的情況下久期就不能完全描述債券價格對利率變動的敏感性。凸性越大,債券價格曲線彎曲程度越大,用修正久期度量債券的利率風險所產生的誤差越大。
修正久期度量了收益率與債券價格的近似線性關係,即到期收益率變化時債券價格的穩定性。在同等要素條件下,修正久期小的債券較修正久期大的債券抗利率上升風險能力強,但抗利率下降風險能力較弱。
久期本身也會隨著利率的變化而變化。所以它不能完全描述債券價格對利率變動的敏感性，1984年Stanley Diller引進凸性的概念。
久期描述了價格-收益率曲線的斜率，凸性描述了曲線的彎曲程度。凸性是債券價格對收益率的二階導數。是對債券久期利率敏感性的測量。在價格－收益率出現大幅度變動時，它們的波動幅度呈非線性關係。由持久期作出的預測將有所偏離。凸性就是對這個偏離的修正。
凸性是對債券價格利率敏感性的二階估計，是對債券久期利率敏感性的測量。在價格-收益率出現大幅度變動時，它們的波動幅度呈非線性關係。由持久期作出的預測將有所偏離。凸性就是對這個偏離的修正。無論收益率是上升還是下降，凸性所引起的修正都是正的。因此如果修正持久期相同，凸性越大越好。
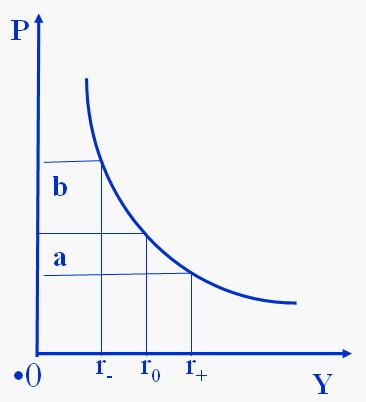
由債券定價定理1與4可知（更多債券定價定理，查看債券定價原理條目），債券價格-收益率曲線是一條從左上向右下傾斜，並且下凸的曲線。下圖中b>a。
債券定價定理1：
債券價格與到期收益率成反向關係。
- 若到期收益率大於息票率，則債券價格低於面值，稱為折價債券（discount bonds）；
- 若到期收益率小於息票率，則債券價格高於面值，稱為溢價債券（premium bonds）；
- 若息票率等於到期收益率，則債券價格等於面值，稱為平價債券（par bonds）。
對於可贖回債券，這一關係不成立。
債券定價定理4：
若債券期限一定，同等收益率變化下，債券收益率上升導致價格下跌的量，要小於收益率下降導致價格上升的量。
例：三債券的面值都為1000元，到期期限5年，息票率7%，當到期收益率變化時。
| 到期收益率(%) | 6 | 7 | 8 |
|---|---|---|---|
| 價格 | 1042.12 | 1000 | 960.07 |
| 債券價格變化率(%) | 4.21 | 0 | -4.00 |
1、凸性隨久期的增加而增加。若收益率、久期不變，票面利率越大，凸性越大。利率下降時，凸性增加。
2、對於沒有隱含期權的債券來說，凸性總大於0，即利率下降，債券價格將以加速度上升；當利率上升時，債券價格以減速度下降。
3、含有隱含期權的債券的凸性一般為負，即價格隨著利率的下降以減速度上升，或債券的有效持續期隨利率的下降而縮短，隨利率的上升而延長。因為利率下降時買入期權的可能性增加了。
債券凸性投資價值的評估[1]
假設我們面對兩個不同期次，具有相同存續期間的政府公債（無信用風險），兩者的市場殖利率也正好相同，投資人對這兩張債券是否會有不同的偏好呢？基於債券凸性的特質，如果兩者有著不同的債券凸率，理性投資人應該會偏好債券凸率較高的公債。因此，在市場供給需求的調整下，我們可以預期兩公債的殖利率必將有所調整，以反應投資人對高凸率公債的偏好。投資人對於高凸率債券的殖利率要求將會低於凸率較小的債券，也就是說，在其他條件相同的情況下，高凸率債券的價格應該比低凸率債券為高，以反應債券凸性的價值。
然而，市場中的債券價格果真有反應出債券凸性的價值嗎？Kahn and Lochoff(1990)使用1981年至1986年的美國公債為樣本，發現債券凸性在某些情況下會給投資人帶來超額投資報酬，也就是說即使投資人以較高的價格購入具有高債券凸率的債券，其投資報酬仍然要比投資於低凸率債券為佳，這顯示出交易市場對於債券凸性的定價並不正確，因此存在有超額獲利空間。Lacey and Nawalkha(1993)則提出了不同的結論。這兩位學者以1976到1987年的美國公債為樣本作分析，結果並未發現高債券凸性會帶給投資人超額的報酬，表示其已被市場正確的定價。
國內在此方面的實證研究也有不少，林聰欽(1995)以國內公債及公司債為樣本，發現債券凸性對於超額投資報酬有解釋能力，李耀宗(1995)針對國內公司債作分析，也發現債券凸性是超額投資報酬的解釋因數之一，顯示出針對債券凸性的操作策略是值得投資人重視的。吳榮昌(1997)使用1992到1996年國內所發行之35期次的政府公債，以時間序列進行橫斷面回歸分析，來測試債券凸性以及其他因數解釋債券超額報酬的能力。該研究結果發現，債券凸性在解釋國內公債超額報酬的能力上並不顯著，再度驗證國內公債市場投資人對於債券凸性並未做出合理定價，這表示市場投資人或可針對債券凸性找出套利機會。
舉例來說，投資人可以透過換券操作，在維持原有的存續期間條件下，將債券投資組合中低凸率債券換為高凸率債券，以獲取更高的投資報酬。以市場中常見的平衡式操作法與單一式操作法為例，由於平衡式債券組合所產生的現金流量較為分散，在存續期間相同的情況下，要比單一式債券組合的凸率要高。如果國內公債市場果真對於凸率的定價不具效率，投資人可以在現有交易的各期次債券中，選取組成一個與目標債券存續期間相當的債券投資組合。由於債券組合之凸率較高，只要該組合的加權平均殖利率與目標債券的殖利率相當，投資人就可以享有更高的預期投資報酬率。而且即使該債券組合的殖利率要比目標債券為低，但是在考量債券凸性的價值後，其預期報酬率仍有可能會比較好.
債券凸性價值與利率波動[1]
債券凸性價值的存在是建基於未來利率的變動，利率變動幅度越大，債券凸性的價值就越高。而如果利率維持不變或變動幅度不 大，以債券凸性為主軸之操作策略效果是不易彰顯的。然而，市場中常用的債券投資報酬衡量，包括殖利率(yield to maturity) ，以及持有期間報酬率(holding period return)等，均是假設利率結構曲線(yield curve)維持不變，利率波動幅度為零，這與實際市場情況大有出入。以一個目前市場殖利率為8%的債券而言，除非投資人持有該債券到期，而且在持有期間內該債券所產生之現金流量均可取得8%的再投資報酬率，否則投資人實際的報酬率將不會等於8%。換句話說，除非利率結構曲線不變，否則該債券的預期報酬率將不會等於殖利率，因此以殖利率為報酬衡量指標的投資決策容易產生偏誤。
持有期間報酬率放寬了投資期間必須等於債券到期期限的限制，衡量投資人在預定之投資期限內的報酬。假設一個殖利率為8%的五年期債券，投資期限設為2年，則持有期間報酬率的計算就是依據這兩年內之債券現金流量，加上兩年後該債券的市場價值來決定。但是未來債券價值的計算仍是以在假設目前殖利率曲線維持不變的情形下所推估出來的遠期利率(forwardrate)來決定。因此持有期間報酬率的正確性仍然取決於未來利率不變的假設。
實際的情況是，未來利率必定會有波動，如果投資人不將此因素納入投資報酬的衡量過程，當然會產生決策上的誤差，而由於債券凸性的存在，利率的波動將會提升債券的價值，因此持有期間報酬率會低估(under-estimate)債券的預期投資報酬率，而誤差的部分就等於債券凸性的價值。
Ilmanen(1995)提出了一個將未來利率波動納入考量的報酬衡量指標，我們稱之為凸性調整後預期報酬(Convexity-adjusted expected return)，該指標定義如 下：
凸性調整後預期報酬＝持有期間報酬率＋債券凸性價值
其中債券凸性價值的衡量是依據債券凸率(Conv)以及預期之殖利率波動程度(Vol(dy))計算如下：
債券凸性價值＝![0.5\times Conv\times [Vol(dy)]^2](/w/images/math/3/5/4/354fad25ad774d2d830ed294a4da214c.png)
舉例來說，如果投資人預期未來市場利率的上下波動幅度為50bp，對於一個凸率為10.75%的債券而言，其債券凸性價值為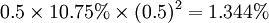
。假設該債券的預期持有期間報酬率為6.35%，則該債券之預期報酬應該是7.694%。以這樣的方法來衡量不同債券的預期投債券凸性的進階探討資報酬將可以強化投資決策的正確性。在下表中，我們比較三個虛擬債券的投資決策，我們可以看到，在其他條件(例如信用風險等)相同情況下，如果單就持有期間報酬率來看，債券B應該是較佳的選擇，但是如果將三個債券各自的債券凸性價值納入考量，債券C反而是更佳之投資標的了。
表(1)：債券凸性調整後報酬率的比較:
| 債券 | 存續期間 | 債券凸率 | 預期持有期間報酬率 | 債券凸性價值 | 凸性調整後報酬率 |
| A | 3.5 | 12.58 | 7.35% | 1.57% | 8.92% |
| B | 3.5 | 10.25 | 7.43% | 1.28% | 8.71% |
| C | 3.5 | 14.37 | 7.16% | 1.80% | 8.96% |
*債券凸性價值的計算假設持有期間利率波動幅度為50bp。
我們可以看到，債券凸性價值的大小取決於兩個因素：債券凸率以及利率波動性。一般而言，長期債券的凸率較小，但是短期利率波動性較高。此外，利率波動結構(volatility structure of interest rate, or volatility curve)也會隨著市場情況而變動，這是投資人在估計利率波動程度時應該特別註意的地方。不過，即使短期利率波動較大，但是由於短期債券的凸率通常很小，即使忽略了債券凸性的考量，對於預期報酬的衡量影響不至於太大。對於長期債券而言，特別是在市場利率波動增較大時，債券凸性的重要性就不容忽視了。 Ilmanen(1995)提出一個簡便的估計法，就是債券凸性價值隨著債券存續期間的平方根增加。舉例來說，凸率相同的兩個債券，如果它們的存續期間分別為1及4，則兩個債券凸性價值的差距大約為兩倍。
債券凸性對利率曲線的影響[1]
除了對投資報酬率的影響之外，債券凸性對於利率期間結構曲線的影響也值得投資人註意。一般而言，市場中不同形狀的利率期間結構曲線反應出了市場
投資人對於未來利率變動的預期。傳統的預期理論（參見：凱恩斯的預期理論、純粹預期理論），流動性溢酬理論(liquidity premium theory)，以及市場區隔理論(Market segmentation theory)均對於殖利率曲線形狀所代表的的內涵提出瞭解釋，而投資人也據此來研擬各種不同的債券操作策略。例如根據即期利率曲線推估出遠期利率(forward rate)，以作為利率交換之定價依據，或者是根據所推估出遠期利率結構曲線(forward rate curve)來作為利率模型的建構基礎等等。
根據我們先前對債券凸性價值的分析，我們知道長期債券由於擁有較高的凸率，在其他條件相同情況下，應較具投資價值。因此，投資人對於長期債券的投資報酬率要求（不論是以殖利率或是持有期間報酬率來看）應該會比較低，以反應債券凸性的價值。如此一來，市場中的殖利率曲線將會隨著債券凸性的進階探討債券期間的增長而產生向下彎曲(Inverted curve)的壓力。我們可以用簡單的預期理論為例子來說明。假設市場人士預期未來利率會逐漸上升，所觀察到的殖利率結構曲線應該是一個向上攀升的曲線，但是由於長期債券的凸率較大，債券凸性價值較高，投資人對長期債券殖利率的要求降低，使得實際觀察到的殖利率曲線會隨著期間的增長而出現下滑的偏誤，學術界將此現象稱之為債券凸性偏誤(Convexity bias)。如果我們不將債券凸性對利率曲線的影響納入考量，而直接使用觀察到的殖利率曲線做投資決策的依據，將會產生偏誤。
以遠期利率的估算為例，假設目前市場中所觀察到的各期次即期利率為表(1)之第一行所示，而各期次債券所產生之凸性偏誤值則顯示在第三行。我可以依據凸性偏誤值反推出真正的即期利率結構曲線，如表中之第四行。如果按照一般慣例使用利率預期理論來推估遠期利率，我們可以看到，使用實際觀察與修正後的即期利率所估計出來的遠期利率（第二行及第五行）結果不大相同。在市場波動性較大時，此種差距會更為顯著。
表(2)：債券凸性偏誤對遠期利率估計之影響
| 期限 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 市場即期利率 | 5.00% | 5.15% | 5.30% | 5.40% | 5.48% | 5.55% | 5.60% | 5.64% |
| 估計之遠期利率 | - | 5.30% | 5.60% | 5.70% | 5.80% | 5.90% | 5.90% | 5.92% |
| 凸性偏誤 | 0.000% | 0.000% | 0.005% | 0.010% | 0.018% | 0.030% | 0.043% | 0.055% |
| 修正後即期利率 | 5.00% | 5.15% | 5.31% | 5.41% | 5.50% | 5.58% | 5.64% | 5.70% |
| 實際之遠期利率 | - | 5.30% | 5.62% | 5.73% | 5.85% | 5.99% | 6.02% | 6.06% |
由於許多債券操作，例如利率交換交易等，需要正確的遠期利率估計值來作為定價的基礎，因此債券凸性偏誤對於利率期間結構曲線的影響值得投資人註意。例如Burgharidt and Hoskins (1995)在一篇研究報告中就指出，市場人士慣用歐元期貨價格來估計遠期利率，以作為利率交換定價的基礎。但是當市場利率波動增加時，由於利率交換價格具有債券凸性，而歐元期貨的價格與報酬關係為線性(凸率為零)，因此傳統的市場操作方式會出現明顯套利機會。簡單來說，投資人只需要放空利率交換（也就是收固定利率，付浮動利率），並放空歐元期貨來避險，便可以無風險的獲取此凸性偏誤的價值。由於該文比較偏重在衍生商品交易之應用，與本文主旨不盡相同，在此不做更進一步的介紹，有興趣的讀者可自行參閱該文。
本条目由以下用户参与贡献
Zfj3000,沙漠之鹰,funwmy,Vulture,Cabbage,Dan,Angle Roh,Yixi,风行水使,泡芙小姐,林巧玲,可恨密码记不住,连晓雾,Tracy,LuyinT,悠影,ElouiseLa.評論(共12條)
有點簡略了，是否可以更充實一點呢？因為凸性對於投資學來講是很重要的一項！
該內容已被Cabbage進行補充完善
哪裡複製的 定理1下來就是定理4了
凸性是從債券的定價定理1和4得到的 所以定理1與定理4不是跳躍 是放上來補充解釋凸性與債券定價的計算關係，可以參考庫里債券定價原理條目，查看更多定理
凸性和票息率的關係到底是？投資組合書上說是inverse relationship，但是百科說的是正相關關係，到底是誰錯了
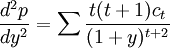
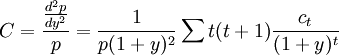
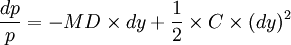
有點簡略了，是否可以更充實一點呢？因為凸性對於投資學來講是很重要的一項！