債券收益率
出自 MBA智库百科(https://wiki.mbalib.com/)
債券收益率(bond yield):就是衡量債券投資收益通常使用的一個指標,是債券收益與其投入本金的比率,通常用年利率表示。債券的投資收益不同於債券利息,債券利息僅指債券票面利率與債券面值的乘積,它只是債券投資收益的一個組成部分。除了債券利息以外,債券的投資收益還包括價差和利息再投資所得的利息收入,其中價差可能為負值。
債券收益率曲線是描述在某一時點上一組可交易債券的收益率與其剩餘到期期限之間數量關係的一條曲線,即在直角坐標系中,以債券剩餘到期期限為橫坐標、債券收益率為縱坐標而繪製的曲線。
決定債券收益率的主要因素,有債券的票面利率、期限、面值、持有時間、購買價格和出售價格。
目錄 |
具體的債券收益率計算公式如下所示:
1、對處於最後付息周期的附息債券(包括固定利率債券和浮動利率債券)、貼現債券和剩餘流通期限在一年以內(含一年)的到期一次還本付息債券,到期收益率採取單利計算。計算公式為:
其中:
- y為到期收益率;
- PV為債券全價(包括成交凈價和應計利息,下同);
- D為債券交割日至債券兌付日的實際天數;
- FV為到期本息和。
其中:
上述公式同樣適用於計算債券回購交易中的回購利率,不過其中FV為到期結算本息和,PV為首期結算金額,D為回購天數。
2、剩餘流通期限在一年以上的零息債券的到期收益率採取複利計算。計算公式為:
其中:
- y為到期收益率;
- PV為債券全價;
- M為債券面值;
- N為債券的剩餘流通期限(年),等於債券交割日至到期兌付日的實際天數除以365。
3、剩餘流通期限在一年以上的到期一次還本付息債券的到期收益率採取複利計算。計算公式為:
其中:
- y為到期收益率;
- PV為債券全價;
- C為債券票面年利息;
- N為債券償還期限(年);
- M為債券面值;
- L為債券的剩餘流通期限(年),等於債券交割日至到期兌付日的實際天數除以365。
4、不處於最後付息周期的固定利率附息債券和浮動利率債券的到期收益率採取複利計算。
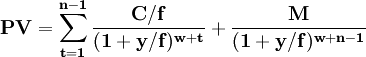
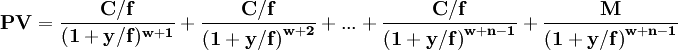
其中:
- y為到期收益率;
- PV為債券全價;
- f為債券每年的利息支付頻率;
- W=D/(365÷f),D為從債券交割日距下一次付息日的實際天數;
- M為債券面值;
- n為剩餘的付息次數;
- C為當期債券票面年利息,在計算浮動利率債券時,每期需要根據參數C的變化對公式進行調整。
上述計算中,除了回購利率以外都是以到期收益率來衡量投資者的債券投資收益。到期收益率是在假設投資者持有債券到期的情況下衡量其債券投資收益的,除此之外,我們還可以用持有期收益率來衡量持有到期前投資者買賣債券的收益。如持有債券期間沒有發生付息,則計算公式與回購利率計算公式相同,其中PV為債券買入全價,FV為債券賣出全價,D為持有債券天數;如持有債券期間發生付息,計算公式詳見附2。
其中:
- y為持有期收益率;
- PV為債券買入全價,
- FV為債券賣出全價;
- f為債券每年的利息支付頻率;
- W=D/(365÷f),
- D為從債券買入交割日距下一次付息日的實際天數;
- v=d/(365÷f),
- d為持有債券期間從最後一次付息日距債券賣出交割日的實際天數;
- m為持有債券期間的付息次數;
- C為當期債券票面年利息。
需要說明的是,上述計算只是停留在理論上的計算,在實際操作過程當中,收益率的計算要考慮購買成本、交易成本、通貨膨脹和稅收成本因素,需要對上述計算公式作相應的調整。
- (一)基礎利率
基礎利率是投資者所要求的最低利率,一般使用無風險的國債收益率作為基礎利率的代表,並應針對不同期限的債券選擇相應的基礎利率基準。
- (二)風險溢價
債券收益率與基礎利率之間的利差反映了投資者投資於非國債的債券時面臨的額外風險,因此也稱為風險溢價。可能影響風險溢價的因素包括:
1.發行人種類。不同的發行人種類代表了不同的風險與收益率,他們以不同的能力履行其合同義務。例如,工業公司、公用事業公司、金融機構、外國公司等不同的發行人發行的債券與基礎利率之間存在一定的利差,這種利差有時也稱為市場板塊內利差。
2.發行人的信用度。債券發行人自身的違約風險是影響債券收益率的重要因素。債券發行人的信用程度越低,投資人所要求收益率越高;反之則較低。
3.提前贖回等其他條款。如果債券發行條款包括了提前贖回等對債券發行人有利的條款,則投資者將要求相對於同類國債來說較高的利差;反之,如果條款對債券投資者有利,則投資者可能要求一個小的利差。
4.稅收負擔。債券投資者的稅收狀況也將影響其稅後收益率,
5.債券的預期流動性。債券的交易有不同程度的流動性,流動性越大,投資者要求的收益率越低;反之則要求的收益率越高。
6.到期期限。由於債券價格的波動性與其到期期限的長短相