馬爾可夫鏈模型
出自 MBA智库百科(https://wiki.mbalib.com/)
馬爾可夫鏈模型(Markov Chain Model)
目錄 |
馬爾可夫鏈因安德烈·馬爾可夫(Andrey Markov,1856-1922)得名,是數學中具有馬爾可夫性質的離散時間隨機過程。該過程中,在給定當前知識或信息的情況下,過去(即當期以前的歷史狀態)對於預測將來(即當期以後的未來狀態)是無關的。
時間和狀態都是離散的馬爾可夫過程稱為馬爾可夫鏈, 簡記為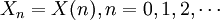 。
。
馬爾可夫鏈是隨機變數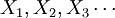 的一個數列。這些變數的範圍,即他們所有可能取值的集合,被稱為“狀態空間”,而Xn的值則是在時間n的狀態。如果Xn + 1對於過去狀態的條件概率分佈僅是Xn的一個函數,則
的一個數列。這些變數的範圍,即他們所有可能取值的集合,被稱為“狀態空間”,而Xn的值則是在時間n的狀態。如果Xn + 1對於過去狀態的條件概率分佈僅是Xn的一個函數,則
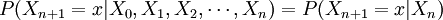
這裡x為過程中的某個狀態。上面這個恆等式可以被看作是馬爾可夫性質。
馬爾可夫在1906年首先做出了這類過程 。而將此一般化到可數無限狀態空間是由柯爾莫果洛夫在1936年給出的。
馬爾可夫鏈與布朗運動以及遍歷假說這兩個二十世紀初期物理學重要課題是相聯繫的,但馬爾可夫尋求的似乎不僅於數學動機,名義上是對於縱屬事件大數法則的擴張。
馬爾可夫鏈是滿足下麵兩個假設的一種隨機過程:
1、t+l時刻系統狀態的概率分佈只與t時刻的狀態有關,與t時刻以前的狀態無關;
2、從t時刻到t+l時刻的狀態轉移與t的值無關。一個馬爾可夫鏈模型可表示為=(S,P,Q),其中各元的含義如下:
1)S是系統所有可能的狀態所組成的非空的狀態集,有時也稱之為系統的狀態空間,它可以是有限的、可列的集合或任意非空集。本文中假定S是可數集(即有限或可列)。用小寫字母i,j(或Si,Sj)等來表示狀態。
2)![P=[P_{ij}]_{n\times n}](/w/images/math/b/7/f/b7fc073dd636d9d6e254290ea4e52a91.png) 是系統的狀態轉移概率矩陣,其中Pij表示系統在時刻t處於狀態i,在下一時刻t+l處於狀態i的概率,N是系統所有可能的狀態的個數。對於任意i∈s,有
是系統的狀態轉移概率矩陣,其中Pij表示系統在時刻t處於狀態i,在下一時刻t+l處於狀態i的概率,N是系統所有可能的狀態的個數。對於任意i∈s,有 。
。
3)![Q=[q_1,q_2\cdots q_n]](/w/images/math/2/c/5/2c53d2360d34a9ced4df0fd38eb805d2.png) 是系統的初始概率分佈,qi是系統在初始時刻處於狀態i的概率,滿足
是系統的初始概率分佈,qi是系統在初始時刻處於狀態i的概率,滿足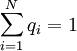 。
。
馬爾可夫鏈是由一個條件分佈來表示的
P(Xn + 1 | Xn)
這被稱為是隨機過程中的“轉移概率”。這有時也被稱作是“一步轉移概率”。二、三,以及更多步的轉移概率可以導自一步轉移概率和馬爾可夫性質:

同樣:
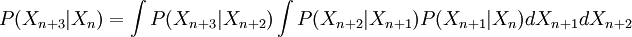
這些式子可以通過乘以轉移概率並求k−1次積分來一般化到任意的將來時間n+k。
邊際分佈P(Xn)是在時間為n時的狀態的分佈。初始分佈為P(X0)。該過程的變化可以用以下的一個時間步幅來描述:
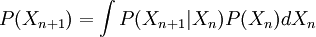
這是Frobenius-Perron equation的一個版本。這時可能存在一個或多個狀態分佈π滿足:
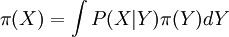
其中Y只是為了便於對變數積分的一個名義。這樣的分佈π被稱作是“平穩分佈”(Stationary Distribution)或者“穩態分佈”(Steady-state Distribution)。一個平穩分佈是一個對應於特征根為1的條件分佈函數的特征方程。
平穩分佈是否存在,以及如果存在是否唯一,這是由過程的特定性質決定的。“不可約”是指每一個狀態都可來自任意的其它狀態。當存在至少一個狀態經過一個固定的時間段後連續返回,則這個過程被稱為是“周期的”。
如果狀態空間是有限的,則轉移概率分佈可以表示為一個具有(i,j)元素的矩陣,稱之為“轉移矩陣”:
Pij = P(Xn + 1 = i | Xn = j)
對於一個離散狀態空間,k步轉移概率的積分即為求和,可以對轉移矩陣求k次冪來求得。就是說,如果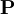 是一步轉移矩陣,
是一步轉移矩陣, 就是k步轉移後的轉移矩陣。
就是k步轉移後的轉移矩陣。
平穩分佈是一個滿足以下方程的向量:

在此情況下,穩態分佈π * 是一個對應於特征根為1的、該轉移矩陣的特征向量。
如果轉移矩陣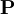 不可約,並且是非周期的,則
不可約,並且是非周期的,則 收斂到一個每一列都是不同的平穩分佈π * ,並且,
收斂到一個每一列都是不同的平穩分佈π * ,並且,
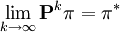
獨立於初始分佈π。這是由Perron-Frobenius theorem所指出的。
正的轉移矩陣(即矩陣的每一個元素都是正的)是不可約和非周期的。矩陣被稱為是一個隨機矩陣,當且僅當這是某個馬爾可夫鏈中轉移概率的矩陣。
註意:在上面的定式化中,元素(i,j)是由j轉移到i的概率。有時候一個由元素(i,j)給出的等價的定式化等於由i轉移到j的概率。在此情況下,轉移矩陣僅是這裡所給出的轉移矩陣的轉置。另外,一個系統的平穩分佈是由該轉移矩陣的左特征向量給出的,而不是右特征向量。
轉移概率獨立於過去的特殊況為熟知的Bernoulli scheme。僅有兩個可能狀態的Bernoulli scheme被熟知為貝努利過程
馬爾可夫鏈通常用來建模排隊理論和統計學中的建模,還可作為信號模型用於熵編碼技術,如演算法編碼。馬爾可夫鏈也有眾多的生物學應用,特別是人口過程,可以幫助模擬生物人口過程的建模。隱蔽馬爾可夫模型還被用於生物信息學,用以編碼區域或基因預測。
馬爾可夫鏈最近的應用是在地理統計學(geostatistics)中。其中,馬爾可夫鏈用在基於觀察數據的二到三維離散變數的隨機模擬。這一應用類似於“克裡金”地理統計學(Kriging geostatistics),被稱為是“馬爾可夫鏈地理統計學”。這一馬爾可夫鏈地理統計學方法仍在發展過程中。
人力資源中的應用
馬爾可夫鏈模型主要是分析一個人在某一階段內由一個職位調到另一個職位的可能性,即調動的概率。該模型的一個基本假設就是,過去的內部人事變動的模式和概率與未來的趨勢大體相一致。實際上,這種方法是要分析企業內部人力資源的流動趨勢和概率,如升遷、轉職、調配或離職等方面的情況,以便為內部的人力資源的調配提供依據。
它的基本思想是:通過發現過去組織人事變動的規律,以推測組織在未來人員的供給情況。馬爾可夫鏈模型通常是分幾個時期收集數據,然後再得出平均值,用這些數據代表每一種職位中人員變動的頻率,就可以推測出人員變動情況。
具體做法是:將計劃初期每一種工作的人數量與每一種工作的人員變動概率相乘,然後縱向相加,即得到組織內部未來勞動力的凈供給量。其基本表達式為:
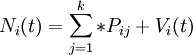
- Ni(t):t時間內I類人員數量;
- Pji:人員從j類向I類轉移的轉移率;
- Vi(t):在時間(t-1,t)I類所補充的人員數。
企業人員的變動有調出、調入、平調、晉升與降級五種。表3 假設一家零售公司在1999至2000年間各類人員的變動情況。年初商店經理有12人,在當年期間平均90%的商店經理仍在商店內,10%的商店經理離職,期初36位經理助理有 11%晉升到經理,83%留在原來的職務,6%離職;如果人員的變動頻率是相對穩定的,那麼在2000年留在經理職位上有11人(12×90%),另外,經理助理中有4人(36×83%)晉升到經理職位,最後經理的總數是15人(11+4)。可以根據這一矩陣得到其他人員的供給情況,也可以計算出其後各個時期的預測結果。假設的零售公司的馬爾可夫分析,見下表:
| 1999~2000 | 商店經理 | 經理助理 | 區域經理 | 部門經理 | 銷售員 | 離職 |
|---|---|---|---|---|---|---|
| 商店經理 (n=12) | 90% 11 | 10% 1 | ||||
| 經理助理 (n=36) | 11% 4 | 83% 30 | 6% 2 | |||
| 區域經理 (n=96) | 11% 11 | 66% 63 | 8% 8 | 15% 14 | ||
| 部門經理 (=288) | 10% 29 | 72% 207 | 2% 6 | 16% 46 | ||
| 銷售員 (=1440) | 6% 86 | 74% 1066 | 25% 228 | |||
| 供給預測 | 15 | 41 | 92 | 301 | 1072 | 351 |
馬爾可夫模型案例分析[1]
- 案例:在信用卡賬戶行為變化預測中的應用
信用卡業務是商業銀行的零售業務,信用卡的消費金額是銀行的應收賬款.在此,我們可以借鑒零售行業應收賬款狀態變化的預測方法對信用卡賬戶的行為變化進行描述和預測。
對信用卡賬戶的馬爾可夫過程進行研究,主要解決新增貸款發生周期性變化的情況下利用馬爾可夫過程預測不同時刻的信用卡賬戶各狀態下的金額、已償付態和壞帳態的金額、全部應收款的現值及它們的方差計算等內容,以為商業銀行信用卡賬戶的行為風險管理提供方法依據。
馬爾可夫狀態轉移模型是在滿足“馬氏性”和“平穩性”的基礎上建立的.假定銀行的信用卡賬戶中每期處於不同期限的逾期貸款數量只與上期逾期貸款的數量與結構有關,而與前期的狀態無關,這就滿足了“馬氏性”。同時,在外部經濟環境穩定、人口特征比較穩定、銀行的信用卡管理技術和方法沒有發生重大變化的情況下,可以認為逾期貸款由一種狀態轉移到另一種狀態的概率在各期是保持不變的,即每年的轉移概率矩陣基本保持穩定,滿足了馬氏鏈的“平穩性”要求.這樣,銀行就可以通過往年的數據資料模擬出比較精確的轉移概率矩陣,對信用卡賬戶的行為狀態做出預測和評估,下麵給出具體分析。
假設某一銀行在時間i有一定的信用卡應收賬款,當前或者隨後的時間內這些餘額都可以劃分為n個時間段(即狀態。對於這批在時間i的應收賬款而言,有:
B0=逾期為0期的應收賬款餘額(也就是當前期);
B1 = 逾期為1期的應收賬款餘額;
…
Bj = 逾期為j期的應收賬款餘額;
…
Bn − 1 = 逾期為n-1期的應收賬款餘額;
Bn = 逾期為n期的應收賬款餘額。
實踐中,時間段的數目將視情況而定,最後一個時間段主要依賴於銀行應收賬款的“沖銷”原則,美國的信用卡貸款一般拖欠180天以上即成為呆賬予以“沖銷”.雖然拖欠賬款最終也可能得到償還,但是將超過規定還款期限的應收賬款歸入壞帳種類中是很自然的會計程式。
一般而言,我們可以讓Bjk表示從i時刻處於j狀態轉移到i+1時刻處於k狀態的賬戶的金額.用這種方法,我們可以對處於i時刻的所有應收賬款做出在i+1時刻的一步轉移賬戶.需要註意的是,還應該有一個“時間”狀態應該加入到先前所描述的分類中,這一狀態就是已付款狀態,用 表示.在i時刻任何一種分類狀態從0到n的賬戶在i+1時刻都可以轉移到狀態
表示.在i時刻任何一種分類狀態從0到n的賬戶在i+1時刻都可以轉移到狀態 .這樣,i時刻的應收賬款賬戶可以用一個n+2維矩陣來表示,矩陣中的每一項Bjk表示i時刻j狀態轉移為i+1時刻k狀態的金額,如下所示:
.這樣,i時刻的應收賬款賬戶可以用一個n+2維矩陣來表示,矩陣中的每一項Bjk表示i時刻j狀態轉移為i+1時刻k狀態的金額,如下所示:
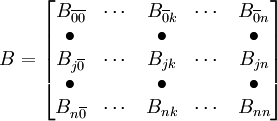
對信用卡賬戶而言,需要註意的是,當狀態Bjk中的j<i時,應理解為i時刻處於狀態j的賬戶,在隨後的i+1時刻(一般為30天後)償還了部分的利息,使得應收賬款(貸款)又轉變為k狀態。
從n+2維應收賬款矩陣B可以導出n+2維轉移概率矩陣P.轉移概率矩陣P中的每一項目表示在特定時間內某一賬戶由一種狀態轉移到另一狀態的可能性.這樣的話,一個隱含假設是,轉移概率矩陣的考察周期和應收賬款分類的考察周期是相同的.一般情況下,轉移概率Pjk表示的是i時刻j狀態的賬款轉移到i+1時刻k狀態賬款的可能性.根據應收賬款矩陣B及Bjk,轉移概率Pjk可被定義為:
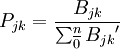
 (1)
(1)
在應用轉移概率矩陣時需要註意兩點。一是 狀態的賬款不可能轉移到其它的狀態,它只能停留在已付款狀態,
狀態的賬款不可能轉移到其它的狀態,它只能停留在已付款狀態, 狀態賬戶的轉移概率依次為:
狀態賬戶的轉移概率依次為: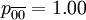 ,
,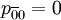 ,
,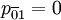 ,…,
,…,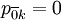 ,…,
,…,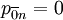 。二是呆賬類賬戶的狀態,雖然有時候壞呆賬類賬款仍能收回現金,但在我們的模型裡邊假設呆賬類賬款只能停留在呆賬類的狀態,即:
。二是呆賬類賬戶的狀態,雖然有時候壞呆賬類賬款仍能收回現金,但在我們的模型裡邊假設呆賬類賬款只能停留在呆賬類的狀態,即: ,pn0 = 0,pn1 = 0,…,pnn = 1.00。
,pn0 = 0,pn1 = 0,…,pnn = 1.00。
上面描述的模型可以被看作一個有n+2個狀態的馬爾可夫鏈過程,其轉移概率矩陣為P.而且,它有兩個吸收態(償付態0和呆賬態n),從其他任何一個暫態(非吸收態)都可以到達這兩個吸收態,因此它是一個具有兩個吸收態的馬爾可夫鏈.我們將在充分利用馬爾可夫理論和已有研究的基礎上,研究如何利用馬爾可夫鏈方法預測和估計信用卡賬戶行為的變化。
在此,採用Kemeny和Snell的部分研究成果.為便於計算,將n+2維轉移概率方陣重新排列,將吸收態的償付態和呆賬態放在一起,將另外的暫態0,1,2,…,n-1放在一起.這樣矩陣P就可以被分割為:
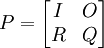
其中I是一個2×2階單位矩陣,O是一個2×n階0矩陣,R是一個n×2階矩陣,Q是一個n×n階矩陣.其中,我們定義矩陣:

一定存在,並將其稱為吸收態馬爾可夫鏈的基本矩陣
對於n×2階矩陣的所有分項,N R給出了每一狀態轉移到吸收態 和n的吸收概率.NR中的第一列給出了每一個狀態轉移到已償付狀態的概率,第二列給出了每一個狀態下轉移到呆賬的概率。
和n的吸收概率.NR中的第一列給出了每一個狀態轉移到已償付狀態的概率,第二列給出了每一個狀態下轉移到呆賬的概率。
1.無新增貸款的情況
假設在時刻i,具有n個分項向量的 給出來每一狀態下應收賬款的餘額.讓b等於所有這些餘額之和,則向量
給出來每一狀態下應收賬款的餘額.讓b等於所有這些餘額之和,則向量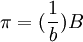 是一個沒有非負分量且全部之和為1的概率向量,向量的分量代表了每一狀態下應收賬款的比例.如果我們假設上述狀態中的餘額的移動是獨立的,那麼我們就可以認定向量π為馬爾可夫鏈的初始向量.另外,還假定:如果A是任一矩陣,那麼我們讓Asq表示A中每一項平方後的結果;讓Art表示A中每一項取平方根後的結果.則有如下結論:
是一個沒有非負分量且全部之和為1的概率向量,向量的分量代表了每一狀態下應收賬款的比例.如果我們假設上述狀態中的餘額的移動是獨立的,那麼我們就可以認定向量π為馬爾可夫鏈的初始向量.另外,還假定:如果A是任一矩陣,那麼我們讓Asq表示A中每一項平方後的結果;讓Art表示A中每一項取平方根後的結果.則有如下結論:
結論1
二維向量BNR中的分量可以給出來自應收賬款向量B的期望還款和壞帳金額;分量給出來償還態和呆帳態的方差,Art給出了這兩種狀態的標準差。
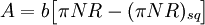 (2)
(2)
證明 如上所述,矩陣NR中第一列的分量給出來應收賬款從每一暫態轉移到吸收態(償付態)的概率.向量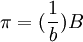 的分量給出了每次過程開始時賬款轉移到每一暫態的初始概率.因此,賬款在最終時償付態的概率可以由向量πNR的第一列分量給出.如果這一過程開始了b次,那麼在最終時償付態的平均數就是向量bπNR = BNR的第一列分量.向量πNR的第一分量是函數f的平均值,其中f表示在最終結束時償付態的價值為全部價值,其它狀態的價值為零.這一函數的方差可以由下式的第一分量給出:
的分量給出了每次過程開始時賬款轉移到每一暫態的初始概率.因此,賬款在最終時償付態的概率可以由向量πNR的第一列分量給出.如果這一過程開始了b次,那麼在最終時償付態的平均數就是向量bπNR = BNR的第一列分量.向量πNR的第一分量是函數f的平均值,其中f表示在最終結束時償付態的價值為全部價值,其它狀態的價值為零.這一函數的方差可以由下式的第一分量給出:
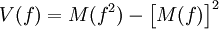
因為f2 = f,所以M(f2) = M(f),因此f的方差可以由πNR − (πNR)sq的第一分量給出.如果過程開始了b次,那麼償付態的全部金額的方差可以由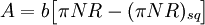 的第一分量給出.有關呆帳態的分析與償付態的分析類似。
的第一分量給出.有關呆帳態的分析與償付態的分析類似。
此外,還可以對應收賬款現值的計算進行了研究. 如果 r是利率,則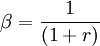 就表示了貼現率,應收賬款現值的計算就可以由下麵的計算給出。
就表示了貼現率,應收賬款現值的計算就可以由下麵的計算給出。
假定B是應收賬款向量,R1是矩陣R的第一列分量,則BR1表示當前時期的收現額;從下一期的BQR1的價值就只有BBQR1;依此類推,在(k+1)周期時BQkR1的價值就只有ΒkBQkR1.將這些折現價值加在一起就可以得到應收賬款的當前現值:
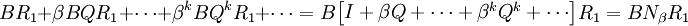 ,其中的Nβ表示
,其中的Nβ表示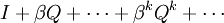 。
。
在實踐當中,銀行一般都要對信用卡客戶收取一定的年費,假定銀行對客戶收取b的費率,則β = 1 + b,那麼完全可以利用上述公式來計算應收賬款的現值.當然,如果考慮利率和年費率兩種因素的話,將會有一個凈折扣率或者一個費用率。
2.新增貸款固定不變的情況
假設每期又發生了金額為c的新應收款,這些新應收款被分不在不同的狀態下,構成了向量C的各分量組成,即: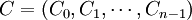 .定義向量
.定義向量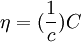 ,則η為概率向量並且被認為是馬爾可夫鏈的初始向量.假設,馬爾可夫過程每期以初始概率η開始了c次.那麼應收賬款的穩定態分佈會怎麼樣,這些賬戶的方差又是多少?每期期望付款和呆賬的數量以及它們的期望方差又怎麼樣?
,則η為概率向量並且被認為是馬爾可夫鏈的初始向量.假設,馬爾可夫過程每期以初始概率η開始了c次.那麼應收賬款的穩定態分佈會怎麼樣,這些賬戶的方差又是多少?每期期望付款和呆賬的數量以及它們的期望方差又怎麼樣?
結論2
如果馬爾可夫過程每期以初始概率η開始了c次,則向量CN的分量給出來所有時刻下穩定的應收賬款金額,數值CNξ給出了穩定態的全部應收賬款金額,其中ξ是各項為1的n維列向量.二維向量CNR給出來每期償付款和呆賬的穩定態的金額。
證明 如果上述馬爾可夫過程進行了許多個周期,則各狀態的金額由當前η一個月前的ηQ、二個月前的ηQ2,等等組成.那麼這些數量之和為:
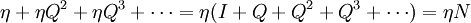
如果這個過程每周期開始了c次,每一狀態下的應收賬款可以由向量cηN = CN表示.如果ξ是一個各項為1的列向量,則CNξ是向量CN的分量之和,代表了應收賬款的全部賬戶餘額.
如果上述過程進行了很多周期,將會有ηR的賬款從第一期的新收款中轉移到吸收態,將有ηQR的賬款從接下來的一期的新收款中轉移到吸收態,將有ηQ2R的賬款從過期兩個月的新收款中轉移到吸收態,依此類推,那麼所有這些之和為:

如果這一過程開始了c次,每期穩定態的償付款和呆賬將有cηNR = CNR給出。證明完畢。
綜合定理1和定理2,我們能夠得出一下推論.讓t = CNξ,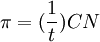 ;那麼CN2R和
;那麼CN2R和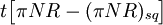 是償付款和呆賬的預測均值和方差.而且,可以根據對應收款的利率和費率來計算應收賬款的現值。
是償付款和呆賬的預測均值和方差.而且,可以根據對應收款的利率和費率來計算應收賬款的現值。
3.新增貸款發生周期性變化的情況
上述討論都沒有考慮應收賬款發生變化的情況,然而,在現實情況下,銀行的信用卡消費呈現出一定的周期性,例如在春節、國慶節和秋季開學的時候消費比較高. 除此之外,商業銀行每年的消費貸款也可能因為經濟增長或蕭條等原因而擴張或收縮. 因此,我們需要考慮這些因素對模型的一些影響.
具體來講,讓Ci是給定月份i的新應收款的向量; ci是全部應收款的金額; η = (1 / ci)Ci是第 i時刻的初始向量,假設:
ηi − T = (ηi) (3)
Ci − T = αCi (4)
其中α是增長繫數的倒數,例如某一貸款機構的信用卡業務以2%的年增長率擴張則α = 1 / (1 + 0.02) = 1 / 1.02T 為迴圈周期的長度,一般情況下周期T = 12. 從上面的兩個式子裡邊我們可以推出ci − T = αci
結論3
讓Nα = (I − αQT) − 1,那麼下列式子:
![A_i= \left[\sum^{r-1}_{k=0}C_{i-k}Q^k\right]N_{\alpha}](/w/images/math/7/1/e/71e50d3cea29810fff927d8391fd6af8.png) (5)
(5)
![\alpha_ii=\left[\sum^{t-1}_{k=0}C_{i-k}Q^k\right]N_{\alpha} \xi](/w/images/math/b/3/8/b38c7444ff887fca8b3ddc2f64ccd0f0.png) (6)
(6)
![D_i=\left[\sum^{t-1}_{k=0}C_{i-k}Q^k\right]N_{\alpha}R](/w/images/math/7/9/f/79f9fc7c01ae161952c3c9ac81bda845.png) (7)
(7)
給出了 i時刻不同狀態下的金額、全部應收賬款、以及吸收態的金額.
證明 讓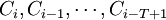 是第i月份及其之前T-1月的真實新收款. 在知道增長率的情況下,根據(4)式能夠推出以前月份的所有應收款,其中第i月份不同狀態的應收款是
是第i月份及其之前T-1月的真實新收款. 在知道增長率的情況下,根據(4)式能夠推出以前月份的所有應收款,其中第i月份不同狀態的應收款是
Ci;第(i-1)月份的是Ci − 1Q;第(i-2) 月份的是Ci − 2Q2,等等; 第(i-T+1) 月份的是
Ci − T + 1QT − 1;第(i-T )月份的是CiQT(Ci − T = αCi),等等. 將這些向量加總後如下:


![= [C_i+C_{i-1}Q+C_{i-2}Q^2+\cdots + C_{i-T+1}Q^{T-1}]N_{\alpha}](/w/images/math/5/1/6/5167b39e45b255ba414199ddbe67c126.png)
這就是Ai,αi和Di的證明與Ai類似.
當然,對於 i時刻的這些估計依賴於第 i月及其前T - 1月的新增應收款,上面給出的估計結果比結論2給出的結果更準確一些. 當然,如果Qn快速趨於0,則用過去幾個月的應收賬款來估計一個合理的結果也是可以的.
根據結論1和結論3的結論,我們可以用AiNR和![\alpha_i\left[\tau_iN R- (\tau_iN R)_{sq}\right]](/w/images/math/5/d/c/5dcac442151a53a6a5dc87d9cbb2a1a2.png) ,其中αi = Aiξ、τi = (1 / alphai)Ai來估計 i時刻償付款和呆帳的均值和方差,而且也可以用AiNβR1用來估計 i時刻應收賬款的現值.
,其中αi = Aiξ、τi = (1 / alphai)Ai來估計 i時刻償付款和呆帳的均值和方差,而且也可以用AiNβR1用來估計 i時刻應收賬款的現值.








好!