大數定律
出自 MBA智库百科(https://wiki.mbalib.com/)
大數定律(Law of Large Numbers)
目錄 |
大數定律是指在隨機試驗中,每次出現的結果不同,但是大量重覆試驗出現的結果的平均值卻幾乎總是接近於某個確定的值。
其原因是,在大量的觀察試驗中,個別的、偶然的因素影響而產生的差異將會相互抵消,從而使現象的必然規律性顯示出來。例如,觀察個別或少數家庭的嬰兒出生情況,發現有的生男,有的生女,沒有一定的規律性,但是通過大量的觀察就會發現,男嬰和女嬰占嬰兒總數的比重均會趨於50%。
定義1:設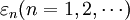 為概率空間(Ω,F,P)上定義的隨機變數序列(簡稱隨機序列),若存在隨機變數
為概率空間(Ω,F,P)上定義的隨機變數序列(簡稱隨機序列),若存在隨機變數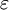 ,使對任意
,使對任意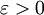 ,恆有:
,恆有:
則稱隨機序列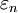 依概率收斂於隨機變數
依概率收斂於隨機變數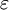 (
(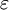 也可以是一個常數),並用下麵的符號表示:
也可以是一個常數),並用下麵的符號表示:
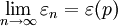 或
或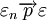
定義2:設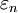 為一隨機序列,數學期望
為一隨機序列,數學期望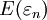 )存在,令
)存在,令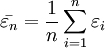 ,若
,若![\lim_{n\to\infty}[\bar{\varepsilon_n}-E(\bar{\varepsilon_n})]=](/w/images/math/b/f/a/bfaf433f620b60488d833822bad07e84.png) 0(P),則稱隨機序列
0(P),則稱隨機序列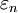 服從大數定律,或者說大數法則成立。
服從大數定律,或者說大數法則成立。
定義3:設Fn(x)是分佈函數序列,若存在一個非降函數F(x),對於它的每一連續點x,都有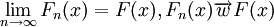 ,則稱分佈函數序列Fn(x)弱收斂於F(x)。
,則稱分佈函數序列Fn(x)弱收斂於F(x)。
定義4:設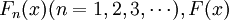 分別是隨機變數
分別是隨機變數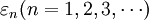 及
及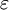 的分佈函數,若
的分佈函數,若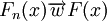 ,則稱
,則稱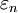 依分佈收斂於
依分佈收斂於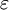 ,亦記為
,亦記為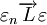 ,且有:(1)若
,且有:(1)若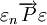 ,則
,則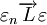 ;(2)設c為常數,則
;(2)設c為常數,則 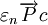 的充要條件是
的充要條件是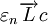 。
。
逆極限定理:設特征函數列fn(t)收斂於某一函數f(t),且f(t)在t=0時連續,則相應的分佈函數列Fn(x)弱收斂於某一分佈函數F(x),而且f(t)是F(x)的特征函數。
大數定律有若幹個表現形式。這裡僅介紹其中常用的兩個重要定律:
(一)切貝雪夫大數定理
設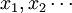 是一列兩兩相互獨立的隨機變數,服從同一分佈,且存在有限的數學期望a和方差σ2,則對任意小的正數ε,有:
是一列兩兩相互獨立的隨機變數,服從同一分佈,且存在有限的數學期望a和方差σ2,則對任意小的正數ε,有:
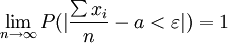
該定律的含義是:當n很大,服從同一分佈的隨機變數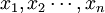 的算術平均數
的算術平均數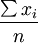 將依概率接近於這些隨機變數的數學期望。
將依概率接近於這些隨機變數的數學期望。
將該定律應用於抽樣調查,就會有如下結論:隨著樣本容量n的增加,樣本平均數將接近於總體平均數。從而為統計推斷中依據樣本平均數估計總體平均數提供了理論依據。
(二)貝努里大數定律
設μn是n次獨立試驗中事件A發生的次數,且事件A在每次試驗中發生的概率為P,則對任意正數ε,有:
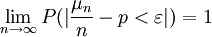
該定律是切貝雪夫大數定律的特例,其含義是,當n足夠大時,事件A出現的頻率將幾乎接近於其發生的概率,即頻率的穩定性。
在抽樣調查中,用樣本成數去估計總體成數,其理論依據即在於此。
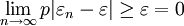
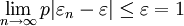








嗯,不錯有很多,很完整,頂。